Minimisation d'un automate fini déterministe
En informatique théorique, et plus particulièrement en théorie des automates, la minimisation d'un automate fini déterministe est l'opération qui consiste à transformer un automate fini déterministe donné en un automate fini déterministe ayant le nombre minimal d'états et qui reconnaît le même langage rationnel. La minimisation a une importance pratique évidente par le gain d'espace qu'elle permet. Il existe plusieurs algorithmes pour effectuer cette opération de minimisation ; les plus usuels sont décrits pour la plupart dans les manuels traitant de théorie des automates[1].
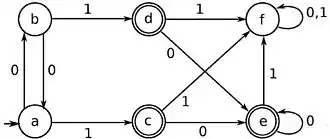
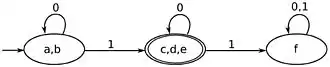
Les algorithmes généraux les plus connus - nommés d'après leurs inventeurs - sont l'algorithme de Brzozowski, l'algorithme de Moore, et l'algorithme de Hopcroft. D'autres algorithmes spécifiques existent, par exemple pour la minimisation d'automates reconnaissant des ensembles finis de mots, comme l'algorithme de Revuz[2] et ses variantes. Les algorithmes ont aussi été étendus à des cas plus généraux, comme les automates avec sortie (automate de Moore, automate de Mealy) ou les transducteurs finis. Il n'existe pas de procédé analogue pour la minimisation d'automates plus généraux, comme les automates à pile ou les automates linéairement bornés.
Une application importante de la minimisation des automates finis déterministes est le test de l'équivalence de deux automates finis, c'est-à-dire le fait de décider s'ils reconnaissent le même langage. C'est une conséquence de l'unicité de l'automate fini minimal, à un renommage des états près. Pour répondre à la question, il suffit de minimiser les deux automates et de tester si leurs versions minimales sont égales.
Étant donné l'importance de la minimisation, cette opération fait partie de la plupart des logiciels de manipulation d'automates.
Automate minimal déterministe
Tout langage rationnel est reconnu par un automate fini déterministe et complet, et parmi ces automates, il en existe un ayant un nombre minimal d'états[3]. Cet automate est unique au renommage des états près; c'est l’automate minimal du langage. L'intérêt d'un automate minimal est que le coût en espace de la représentation est minimisé.
Parmi les automates finis reconnaissant un langage donné, il peut exister des automates non déterministes qui reconnaissent ce langage, et qui ont exponentiellement moins d'états que l'automate fini déterministe minimal. L'adjectif minimal s'applique ici aux automates déterministes[2]. De même, il peut exister des automates non déterministes non isomorphes ayant un nombre minimal d'états et reconnaissant le même langage[2]. L'unicité de l'automate déterministe minimal est donc une propriété remarquable, valable uniquement dans ce cas.
Les automates considérés dans ce cadre sont non seulement déterministes, mais aussi complets. Un automate est complet si sa fonction de transition est partout définie, en d'autres termes si, pour tout état et toute lettre, il existe une transition sortant de cet état et étiquetée par cette lettre. Un automate fini déterministe émondé peut avoir un état de moins, si l'automate fini complet correspondant a un état puits.
États accessibles
On considère un automate fini déterministe complet
sur un alphabet . Ici est l'ensemble des états, est l'état initial, est l'ensemble des états terminaux. La fonction de transition est notée par un simple point. Un état est accessible s'il existe un mot tel que , il est inaccessible sinon. Les états inaccessibles peuvent être supprimés sans modifier le langage reconnu par l'automate, et l'automate minimal ne possède que des états accessibles. Un automate est accessible si tous ses états sont accessibles.
Les états accessibles d'un automate peuvent être calculés au moyen d'un parcours du graphe qui représente l'automate. Ce sont les états qui sont atteints par un chemin depuis l'état initial. Il suffit donc d'adapter l'algorithme usuel de parcours d'un graphe à ce cas. La complexité en temps de l'algorithme est linéaire en fonction du produit du nombre d'états par la taille de l'alphabet. Le code suivant en est une réalisation :
let états_accessibles:= {i};
let états_nouveaux:= {i};
do {
temp := l'ensemble vide;
for each q in états_nouveaux do
for all a in A do
temp := temp ∪ {q.a)};
end;
end;
états_nouveaux := temp \ états_accessibles;
états_accessibles := états_accessibles ∪ états_nouveaux;
} while(états_nouveaux ≠ the empty set);
état_inaccessibles := Q \ états_accessibles;
États indistinguables
Soit
un automate déterministe complet. Deux états et sont indistinguables ou inséparables si tout mot reconnu par à partir de est aussi reconnu à partir de et réciproquement, formellement si pour tout mot :
- .
Deux états sont séparables s'ils ne sont pas inséparables. Un critère de minimalité utile est le suivant :
Critère de minimalité — Un automate fini déterministe complet et accessible est minimal si et seulement ses états sont deux-à-deux séparables.
Une façon plus condensée de présenter ce critère est d'introduire les langages à droite (« right languages » en anglais[2]) : le langage à droite d'un état est par définition le langage
- .
C'est donc l'ensemble des mots reconnus par l’automate en prenant comme état initial. Alors deux états sont inséparables si et seulement s'ils ont même langage à droite.
L'équivalence de Nerode est la relation, notée , sur l'ensemble des états définie par
- .
Deux états équivalents pour l'équivalence de Nerode sont donc indistinguables et réciproquement. Un automate est donc minimal, d'après l'énoncé ci-dessus, exactement quand son équivalence de Nerode est l’égalité.
Ne pas confondre cette équivalence, définie sur les états, avec la relation de Myhill-Nerode, du théorème de Myhill-Nerode, qui est définie sur les mots : deux mots sont équivalents pour la relation de Myhill-Nerode s'ils définissent le même résiduel ou quotient à droite. Les états de l’automate minimal sont en bijection avec les classes de l'équivalence de Myhill-Nerode.
Un algorithme élémentaire
Un algorithme élémentaire de minimisation d'un automate fini déterministe consiste à chercher des paires d'états inséparables ou indistinguables. Cette méthode se trouve dans le manuel de Hopcroft, Motwani et Ullman[4] et celui de Peter Linz[5].
Algorithme de recherche d'états séparables
La méthode est un algorithme de marquage. Elle consiste à chercher et marquer des paires d'états séparables. Elle procède les paires d'états distincts comme suit :
- Pour toute paire d'états, si est final et ne l'est pas ou vice-versa, marquer comme séparables.
- Répéter l'opération suivante tant qu'une nouvelle paire a été marquée :
- Pour toute paire et toute lettre , calculer et . Si la paire est marquée comme étant séparable, marquer comme séparable.
Méthode de remplissage de table
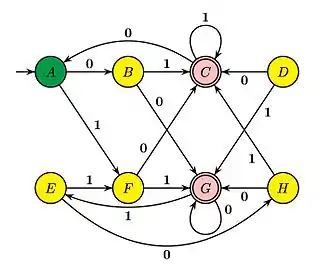
Hopcroft et. al.[6] appellent « table-filling algorithm » (« algorithme de remplissage de table ») la mise en œuvre de l'algorithme qui consiste à remplir une table par inspection progressive des cases. Dans la table ci-dessous, une croix en case (X,Y) signifie que les états X et Y sont séparables. L'exemple suivant se trouve dans leur livre :
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| B | x | |||||||
| C | x | x | ||||||
| D | x | x | x | |||||
| E | x | x | x | |||||
| F | x | x | x | x | ||||
| G | x | x | x | x | x | x | ||
| H | x | x | x | x | x | x |
La première étape consiste à marquer d'une croix les paires (X,Y) où X est final et Y ne l'est pas et vice-versa. Ensuite, on peut marquer l'entrée (B,A) parce que leurs images par la lettre 0 est séparable. On continue autant que possible. Les cases restées non marquées désignent des états inséparables. Ici, cela signifie donc que A et E sont indistinguables, de même que B et H et D et F.
L'algorithme de remplissage est similaire aux autres algorithmes de raffinement décrits ci-dessous. Il est facile à mettre en œuvre à la main sur de petits exemples, mais sa complexité en place et en temps est considérable, sauf à organiser l'exploration de manière disciplinée, auquel cas on se rapproche de la méthode de Moore.
Algorithme de Brzozowski
Brzozowski présente, dans son article de 1963[7], un algorithme de minimisation qui est basé sur la déterminisation d'un automate fini non nécessairement déterministe. Cet algorithme, conceptuellement simple, produit - de façon étonnante - un automate minimal.
La notion importante de l'algorithme est celle d'automate transposé : on modifie l'automate en échangeant les états finaux et initiaux, et en changeant le sens des transitions.
L'énoncé précis est le suivant :
Théorème — Soit un automate fini déterministe et accessible, et soit l'automate fini déterministe complet accessible obtenu à partir de l'automate transposé par déterminisation et élimination des états inaccessibles. Alors l'automate est minimal et reconnaît le langage miroir du langage reconnu par .
L'algorithme de minimisation d'un automate fini est alors le suivant :
- Calculer , en transposant l'automate puis en le déterminisant par la procédure usuelle par exemple qui ne conserve que les états accessibles;
- Répéter l'opération sur l'automate obtenu : calculer en transposant puis en le déterminisant de la même manière.
Pour la deuxième étape, l'automate est déterministe et accessible. Par la proposition de Brzozowski, l'automate obtenu est l'automate minimal équivalent à l’automate de départ. La complexité en temps et en place de l'algorithme est exponentielle dans le pire des cas en fonction de la taille de l'automate de départ, car l'automate intermédiaire peut être exponentiel. Un exemple est fourni par le langage formé de mots de longueur au moins sur un alphabet à deux lettres et , et dont la -ième lettre toujours un , en d'autres termes :
- .
Ce langage est reconnu par un automate à états plus un état puits, mais son transposé, une fois déterminisé, requiert états[2],[8].
Il a été observé[2] que dans la pratique l'algorithme donne des résultats meilleurs que l'on pourrait penser. Ceci pose la question de la complexité en moyenne de l’algorithme. Un article de De Felice et Nicaud[9] apporte une réponse à cette question : l'algorithme de Brzozowski est génériquement super-polynomial. Ce terme technique signifie la complexité en moyenne, et même que la complexité générique de l'algorithme est plus grande que tout polynôme. Le terme « complexité générique » signifie que l'on est autorisé à « ignorer », dans le calcul de la moyenne, un ensemble de cas particulièrement désavantageux, sous réserve que cet ensemble de cas soit de taille négligeable en un sens que l'on peut préciser.
Algorithmes de raffinements de partitions
Principe
Les algorithmes de Moore et de Hopcroft sont des algorithmes de raffinements de partitions. On commence, dans les deux algorithmes, avec une hypothèse naïve, en supposant que l'automate minimal n'a que deux états et, en examinant la fonction de transition, on raffine la partition initiale tant que c'est nécessaire. Le raffinement consiste à trouver des états séparables au sens défini ci-dessus : deux états et sont séparables s'il existe un mot tel que l'état est final et n'est pas final, ou vice-versa.
Lorsque l'algorithme de raffinement s'arrête, chaque classe de la partition représente un ensemble d'états deux-à-deux inséparables, et deux classes distinctes sont séparables. L'automate minimal est obtenu en prenant comme états les classes de la partition, et comme transitions les transitions induites sur les classes par les transitions de l'automate de départ.
Algorithme de Moore
L'algorithme de Moore pour la minimisation d'automates est dû à Moore 1956. L'algorithme maintient une partition des états, constituée initialement de deux classes, formées des états terminaux et des autres. La partition est ensuite raffinée jusqu'à obtenir une partition stable. À chaque étape, on remplace la partition courante par la partition qui est l'intersection de la partition courante et des partitions induites par les préimages des classes par les lettres de l'alphabet. L'algorithme s'arrête lorsque ce remplacement ne modifie pas la partition courante. On montre que les classes de la partition finale sont constituées d'états inséparables, et forment donc les états de l'automate minimal.
L'algorithme est décrit par le pseudo-code suivant :
P := {F, Q \ F};
répéter
P'=P
pour chaque a de A faire
calculer le raffinement de P induit par a;
remplacer P par son intersection avec ces raffinements
jusqu'à P=P'
On considère les équivalences sur l’ensemble des états définies par
- ,
où
- .
Chaque ensemble est donc composé des mots de longueur au plus qui mènent de l'état à un état terminal de l’automate. Deux états sont équivalents pour la relation si les mêmes mots de longueur au plus mènent à des états terminaux. Cela signifie que l'on peut pas les séparer par des mots de longueur au plus . Les équivalences sont parfois appelées équivalences de Moore d'ordre [2]. Ces équivalences se calculent facilement grâce à la propriété suivante :
Lemme — Pour deux états et et , on a
- .
Ainsi, pour calculer l'équivalence , on détermine les états qui, par une lettre, arrivent dans des classes distinctes de : ceux-ci sont dans des classes distinctes de . Plus précisément, on détermine, pour toute lettre , la partition dont les classes sont constituées d'états qui, par la lettre , donnent des états équivalents pour . On forme ensuite l'intersection de ces partitions avec la partition elle-même.
Il est facile de vérifier que si et sont égales pour un entier , alors et sont égales pour tout , et que les classes d'équivalences sont formées d'états inséparables.
La complexité en temps de l'algorithme est, dans le pire des cas, , où est la taille de l'alphabet et où est le nombre d'états de l'automate. Chacune des étapes du raffinement peut être effectuée en temps en utilisant une variante appropriée du tri par base ou « radix sort ». À chaque étape, le nombre de classes augmente strictement, et comme au départ il y a deux classes, au plus étapes suffisent. En fait, la complexité est même en , où est le nombre d'étapes de l'algorithme. On peut observer[2] que le nombre d'étapes est indépendant du nombre d'états de l'automate de départ.
La complexité en moyenne est bien meilleure. Elle est en , et même en , selon le choix du modèle retenu pour la distribution aléatoire[2].
Algorithme de Hopcroft
L'algorithme, appelé ainsi d'après son inventeur, est dû à John Hopcroft[10] et il a été présenté en 1971; il opère par raffinement successif d'une partition initialement grossière de l'ensemble des états de l'automate déterministe fini à minimiser.
Principe
L'algorithme débute avec la partition la plus grossière, dont les deux classes sont composées des états terminaux et des autres. La partition est progressivement raffinée en un nombre croissant de classes plus petites. Chaque tour de l'algorithme partage des ensembles d'états en deux parties plus petites.
L'opération de base est la coupure (« splitting » en anglais)[11]. Un ensemble d'états est coupé par la paire formée d'un ensemble et d'une lettre si les ensembles
- et
sont tous les deux non vides. Dans le cas contraire, on dit que est stable pour .
L'algorithme maintient un ensemble de couples , candidats à couper des éléments de la partition en cours; cet ensemble de candidats en attente est appelé le « waiting set » en anglais.
L'algorithme est décrit par le pseudo-code suivant :
P := {F, Q \ F}; "Partition initiale"
W := l'ensemble vide; "Candidats en attente"
for each a in A do
ajouter (min(F, Q\F),a) à W; "Initialisation de l'ensemble W"
while (W ≠ l'ensemble vide) do
choisir ensemble (Z,a) dans W et l'enlever de W
for each X de P coupé par (Z,a) en X' et X'' do "Calcul de la coupe"
remplacer X in P par les deux ensembles X' et X'' "Raffinement de la partition"
for each b in A do "Mise-à-jour de l'ensemble"
if (X,b) est in W "des candidats en attente"
remplacer (X,b) in W par (X',b) et (X'',b)
else
ajouter le plus petit de (X',b) et (X'',b) à W;
end;
end;
end;
Le but de l'algorithme est d'obtenir par coupes successives un automate déterministe minimal. L'algorithme procède en testant la stabilité de chaque groupe d'états de la partition par toutes les coupes possibles.
L'algorithme débute avec la partition composée de l'ensemble des états terminaux et de l'ensemble des états non terminaux . est l'ensemble des candidats en attente pour raffiner la partition . On ajoute à tout couple de la forme , avec une lettre et le plus petit des ensembles et .
L'algorithme choisit itérativement un ensemble dans l'ensemble des candidats en attente , le retire de l'ensemble et, pour chaque partie de la partition courante, il teste si est coupé par . Dans l’affirmative, la partition est mise à jour en remplaçant par les deux parties et résultant de la coupure. De plus, l'ensemble des candidats en attente est augmenté, pour toute lettre , de et ou du plus petit de et , selon que est dans ce waiting set ou non.
A chaque itération, soit l'ensemble perd un élément, soit la partition est raffinée. Comme la partition ne peut être raffinée indéfiniment parce que l'automate est fini, le nombre d'itérations est donc fini. Ceci prouve donc la terminaison de l'algorithme.
Complexité et optimalité
La complexité en temps de l’algorithme de Hopcroft, dans le pire des cas, est où est le nombre d'états de l'automate et est la taille de l'alphabet. La borne est conséquence du fait que, pour chacune des transitions de l'automate, les ensembles retirés du waiting set qui contiennent l'état d'arrivé d'une transition ont une taille diminuée de moitié au moins à chaque fois, donc chaque transition participe à au plus étapes de coupure dans l'algorithme.
L'algorithme de Hopcroft est le plus efficace des algorithmes de minimisation connus en 2010[2]. L'algorithme initial demande que l'automate de départ soit déterministe et complet. On peut adapter l'algorithme au cas des automates déterministes finis incomplets[12]. L'implémentation est en temps , où est le nombre de transitions de l'automate. On a toujours .
Il reste un certain degré de liberté dans le choix du candidat que l'on retire de l'ensemble des candidats en attente. Cela dépend aussi du choix de la structure de donnée choisie : l'ensemble peut être par exemple organisé en pile (structure LIFO) ou en file (structure FIFO). Il a été prouvé qu'un choix approprié de la stratégie permet à l'algorithme de Hopcroft d'être toujours meilleur que l'algorithme de Moore[2]. En particulier, l'algorithme a une complexité en moyenne en .
Minimisation d'automates non déterministes
Les algorithmes décrits ci-dessus ne s'appliquent pas à des automates non déterministes. Alors que la notion d'automate minimal, compris comme automate ayant un nombre minimal d'états, a parfaitement un sens dans le cas des automates non déterministes, l'unicité n'est plus assurée, et le problème général est PSPACE-complet au sens de la théorie de la complexité[13],[14].
Notes et références
- Carton 2008, Sakarovitch 2003 sont des livres standards en français, Séébold 1999 contient des exercices détaillés ; Hopcroft, Motwani et Ullman 2007 est une référence anglaise.
- Berstel et al. 2010.
- Hopcroft, Motwani et Ullman 2007, Section 4.4.3, "Minimization of DFA's", p. 159.
- Hopcroft, Motwani et Ullman 2007, Section 4.4.1
- Linz 2011, Section 2.4.
- Hopcroft, Motwani et Ullman 2007, p. 157.
- Brzozowski 1963
- D'autres exemples sont donnés dans divers manuels, et aussi, parmi les plus anciens, dans Leiss 1981 pour un alphabet ternaire où états sont requis pour un automate de départ de n états.
- De Felice et Nicaud 2013.
- Hopcroft 1971.
- Le terme coupure est employé par Carton 2008, p. 49.
- Anti Valmari, « Fast brief practical DFA minimization », Information Processing Letters, vol. 112, no 6, , p. 213-217 (DOI 10.1016/j.ipl.2011.12.004).
- Hopcroft, Motwani et Ullman 2007, Section 4.4, p. 163, Encadré intitulé Minimizing the States of an NFA.
- Henrik Björklund et Wim Martens, « The Tractability Frontier for NFA Minimization », Colloquium Theoretische Informatik Universität Bayreuth, (consulté le ).
Bibliographie
- Articles historiques
- Janusz Brzozowski, « Canonical regular expressions and minimal state graphs for definite events », dans Proc. Sympos. Math. Theory of Automata (New York, 1962), Polytechnic Press of Polytechnic Inst. of Brooklyn, Brooklyn, N.Y., (Math Reviews 0175719), p. 529–561.
- Edward F. Moore, « Gedanken-experiments on sequential machines », dans Automata studies, Princeton, N. J., Princeton University Press, coll. « Annals of mathematics studies » (no 34), (Math Reviews 0078059), p. 129–153.
- John Hopcroft, « An n log n algorithm for minimizing states in a finite automaton », dans Theory of machines and computations (Proc. Internat. Sympos., Technion, Haifa, 1971), New York, Academic Press, (Math Reviews 0403320), p. 189–196
- Manuels
- Alfred V. Aho, John E. Hopcroft et Jeffrey D. Ullman, The Design and Analysis of Computer Algorithms, Addison-Wesley, , p. 157–162 (Chapitre 4.13 Partitioning).
- Jean Berstel, Luc Boasson, Olivier Carton et Isabelle Fagnot, « Minimization of Automata », dans Automata: from Mathematics to Applications, European Mathematical Society, (arXiv 1010.5318)
- Olivier Carton, Langages formels, calculabilité et complexité, [détail de l’édition] (lire en ligne)
- (en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, , 3e éd. (ISBN 978-0-32146225-1)
- Jacques Sakarovitch, Éléments de théorie des automates, Paris, Vuibert, , 816 p. (ISBN 2-7117-4807-3, zbMATH 1188.68177)
- Patrice Séébold, Théorie des automates : Méthodes et exercices corrigés, Vuibert, , 198 p. (ISBN 978-2-7117-8630-5)
- Peter Linz, An Introduction to Formal Languages and Automata, Sudbury, MA, Jones & Bartlett Publishers, , 5e éd., 437 p. (ISBN 978-1-4496-1552-9, lire en ligne).
- Autres références
- Cezar Câmpeanu, Karel Culik II, Kai Salomaa et Sheng Yu, « State Complexity of Basic Operations on Finite Languages », dans 4th International Workshop on Automata Implementation (WIA '99), Springer-Verlag, coll. « Lecture Notes in Computer Science » (no 2214), (DOI 10.1007/3-540-45526-4_6), p. 60–70.
- Ernst Leiss, « Succinct representation of regular languages by Boolean automata », Theoretical Computer Science, vol. 13, no 3, , p. 323–330 (DOI 10.1016/S0304-3975(81)80005-9, Math Reviews 603263).
- Sven De Felice et Cyril Nicaud, « Brzozowski Algorithm Is Generically Super-Polynomial for Deterministic Automata », dans Marie-Pierre Béal et Olivier Carton (éditeurs), Developments in Language Theory - 17th International Conference, Springer-Verlag, coll. « Lecture Notes in Computer Science » (no 7907), (ISBN 978-3-642-38770-8, DOI 10.1007/978-3-642-38771-5_17), p. 179-190
- Tsunehiko Kameda et Peter Weiner, « On the state minimization of nondeterministic finite automata », IEEE Transactions on Computers, vol. 100, no 7, (DOI 10.1109/T-C.1970.222994).
- Timo Knuutila, « Re-describing an algorithm by Hopcroft », Theoretical Computer Science, vol. 250, nos 1-2, , p. 333–363 (DOI 10.1016/S0304-3975(99)00150-4, Math Reviews 1795249).
- (en) Norbert Blum, « An O(n log n) implementation of the standard method for minimizing n-state finite automata », Information Processing Letters, vol. 57, no 2, , p. 65–69 (DOI 10.1016/0020-0190(95)00199-9).
- (en) David Gries, « Describing an algorithm by Hopcroft », Acta Informatica, vol. 2, no 2, , p. 97-109 (DOI 10.1007/BF00264025).
- Portail de l'informatique théorique