Modèle de Barabási-Albert
Le modèle de Barabási–Albert (BA) est un algorithme pour la génération aléatoire de réseaux sans échelle à l'aide d'un mécanisme d'attachement préférentiel. On pense que plusieurs systèmes naturels ou humains, tel que l'Internet, le world wide web, les réseaux de citations, et certains réseaux sociaux sont approximativement sans échelle. Ils contiennent en tout cas quelques nœuds (appelés hubs ou moyeux) avec un degré inhabituellement élevé par rapport aux autres nœuds du réseau. Le modèle BA tente d'expliquer l'existence de tels nœuds dans de véritables réseaux. L'algorithme est nommé d'après ses inventeurs Albert-László Barabási et Réka Albert et est un cas particulier d'un modèle plus général appelé modèle de Price[1]
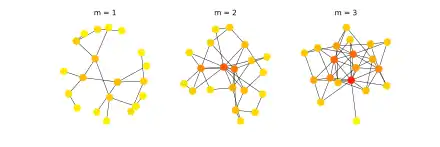
Concepts
La plupart des réseaux observés font partie de la catégorie des réseaux "sans échelle" (au moins approximativement), ce qui signifie que la distribution des degrés de leurs nœuds suit une loi de puissance (scale-free), soulignons que pour des modèles aléatoires tels que le modèle Erdős–Rényi (RE) ou le modèle de Watts–Strogatz (WS) cette distribution ne suit pas une telle loi. Le modèle de Barabási–Albert est l'un des nombreux modèles proposés qui génèrent des réseaux "sans échelle". Il intègre deux concepts importants : la croissance et l' attachement préférentiel. Ces deux mécanismes étant très présent dans de véritables réseaux.
La croissance signifie que le nombre de nœuds dans le réseau augmente au fil du temps.
L'Attachement préférentiel signifie que plus le degré d'un nœud est grand, plus ce nœud est susceptible de recevoir de nouveaux liens. Les nœuds de haut degré ayant une plus grande capacité à « saisir » les liens ajoutés au réseau. Intuitivement, l'attachement préférentiel peut être comprise si l'on raisonne en termes de connexions au sein de réseaux sociaux. Dans ce cas un lien de A vers B signifie que la personne A "connait" ou "est familier avec" la personne B. Les nœuds fortement liés (donc de fort degré) représentent les gens bien connu avec de nombreuses relations. Quand un nouveau venu entre dans la communauté, il est plus susceptible de se familiariser avec l'une de ces personnes très visible plutôt qu'avec un autre moins connu. Le modèle de BA a été proposé en supposant que dans le World Wide Web, les nouvelles pages se liaient préférentiellement à de tels nœuds concentrateurs, c'est-à-dire des sites très bien connu tels que Google, plutôt que vers les pages que presque personne ne connaît. Si quelqu'un choisit de se lier à une nouvelle page en choisissant au hasard un lien existant, la probabilité de sélection d'une page en particulier serait proportionnelle à son degré. Le modèle de BA prétend que c'est ce qui explique la règle dit de l'attachement préférentiel. Toutefois, en dépit d'être un modèle utile, les preuves empiriques suggèrent que le mécanisme dans sa forme la plus simple ne s'applique pas au World Wide Web, comme indiqué dans la « Technical Comment to 'Emergence of Scaling in Random Networks' »
Le modèle de Bianconi–Barabási cherche à répondre à cette question par l'introduction d'un paramètre de « fitness ». L'attachement préférentiel est un exemple de cycle de rétroaction positive où des variations initialement aléatoires (un nœud qui commencerait avec plus de liens ou en ayant accumulé plus tôt qu'un autre) sont automatiquement renforcé, grossissant ainsi grandement les différences. C'est aussi parfois appelé l'effet Matthew : "les riches deviennent plus riches" (Mt 13:12 & 25:29).
Algorithme
Le réseau commence par un premier réseau complètement connecté de nœuds.
De nouveaux nœuds sont ajoutés au réseau. Chaque nœud est connecté à nœuds existants, avec une probabilité proportionnelle au nombre de liens que ces nœuds existants ont déjà. Formellement, la probabilité que le nouveau nœud est connecté à un nœud est[2]
où est le degré du nœud et la somme est faite sur tous les nœuds existants (le dénominateur parcourt donc deux fois le nombre d'arêtes dans le réseau). Les nœuds fortement liés ("hubs" ou "moyeux") ont tendance à accumuler rapidement encore plus de liens, tandis que les nœuds avec seulement quelques liens sont peu susceptibles d'être choisi comme destination pour un nouveau lien. Les nouveaux nœuds ont donc une "préférence" pour s'attacher aux nœuds déjà fortement liés.
Propriétés
Degré de distribution
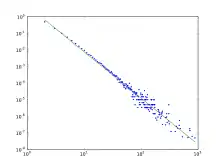
Le degré de la distribution résultant du modèle de BA est sans-échelle, en particulier, c'est une loi de puissance de la forme :
Répartition de l'indice de Hirsch
Le h-index ou indice de Hirsch de distribution a été montré pour être aussi sans-échelle et a été proposé comme l'« index lobby », pour être utilisé comme une mesure de la centralité[3]
En outre, un résultat analytique de la densité de nœuds avec un h-index de 1 peut être obtenu dans le cas où
Moyenne de longueur de chemin d'accès
La distance moyenne entre deux nœuds d'un graphe de BA augmente approximativement comme le logarithmique de la taille du réseau. La formule exacte a une correction en double logarithmique[4] :
Le modèle de BA a une distance moyenne systématiquement plus courte qu'un graphe aléatoire.
Corrélations dans le degré des nœuds
Des corrélations entre les degrés des nœuds connectés se développent spontanément dans le modèle de BA en raison de la manière dont le réseau évolue. La probabilité, , de trouver un lien qui relie un nœud de degré > pour ancêtre un nœud de degré dans la BA, le modèle pour le cas particulier de est donnée par
ce n'est certainement pas le résultat escompté si les distributions n'étaient pas corrélés, .
Pour quelconque, la fraction de liens qui se connectent à un nœud de degré pour un nœud de degré est[5]
De plus, la distribution du degré des plus proches voisins , c'est-à-dire la distribution du degré des plus proches voisins d'un nœud de degré , est donnée par :
En d'autres termes, si l'on sélectionne un nœud de degré , puis l'un de ses voisins au hasard, le degré l de ce nœud suit la loi de probabilité ci-dessus.
Coefficient de clustering
Alors qu'il n'y a pas de résultat analytique pour le coefficient de clustering du modèle de BA, il a été déterminé empiriquement que ces coefficients sont nettement plus élevés pour le modèle de BA que pour des réseaux aléatoires. Le coefficient de clustering évolue également avec la taille du réseau en suivant approximativement une loi de puissance :
Des résultats analytiques pour le coefficient de clustering du modèle de BA ont été obtenus par Klemm et Eguíluz[6] et prouvé par Bollobás[7]. Une approche par champ a de plus été appliquée par Fronczak, Fronczak et Holyst[8].
Ce comportement est toujours distinct du comportement de réseau petit-monde pour lesquels le clustering est indépendant de la taille du système. Dans le cas de réseaux hiérarchiques, le coefficient de clustering suit également une loi de puissance en fonction du degré,
Ce résultat a été obtenu analytiquement par Dorogovtsev, Goltsev et Mendes[9].
Propriétés spectrales
La densité spectrale du modèle de BA a une forme différente du fameux demi-cercle caractérisant la densité spectrale d'un graphe aléatoire. Il dispose d'une forme en triangle dont la pointe se trouve bien au-dessus du demi-cercle et dont les bords décroissent comme une loi de puissance[10].
Dynamique de mise à l'échelle
Par définition le modèle de BA décrit un phénomène en développement et, par conséquent, en plus de son caractère sans-échelle, on pourrait aussi étudier sa dynamique temporelle. Dans le modèle de BA, les nœuds du réseau peuvent également être caractérisée par leur degré généralisé : le produit de la racine carrée du temps de son ajout au réseau et de son degré au lieu du degré seul. En effet de moment de naissance est important dans le modèle de BA. On constate alors que la distribution de ce degré généralisé possède des caractéristiques non-triviales et en particulier une mise à l'échelle dynamique
Cela implique que les différentes courbes de en fonction de se superposeraient sur une courbe universelle si nous tracions en fonction de[11].
Cas limite
Modèle A
Le Modèle A conserve la croissance, mais ne comprend pas l'attachement préférentiel. La probabilité de raccordement d'un nouveau nœud est alors uniforme. La distribution des degrés résultante dans cette limite est géométrique[12], ceci indique que la croissance seule n'est pas suffisante pour produire une structure sans-échelle.
Modèle B
Le Modèle B conserve l'attachement préférentiel, mais élimine la croissance. Le modèle commence avec un nombre fixe de nœuds non connectés et ajoute des liens, en choisissant de préférence les nœuds de haut degré comme lien d'attachement. Bien que le degré de distribution au début de la simulation est sans échelle, la distribution n'est pas stable, et elle finit par devenir presque Gaussienne lorsque le réseau approche de la saturation. Donc L'attachement préférentiel seul n'est donc lui non plus pas suffisant pour produire une structure sans-échelle.
L'échec des modèles A et B pour reproduire une distribution sans-échelle indique que la croissance et l'attachement préférentiel sont nécessaires simultanément pour reproduire la loi de puissance observée dans les réseaux réels.
Histoire
La première utilisation d'un mécanisme d'attachement préférentiel pour expliquer la loi de puissance des distributions semble avoir été dû à Yule en 1925[13]. La méthode moderne de l'équation-maîtresse, qui donne une plus grande transparence à cette dérivation, a été appliquée au problème par Herbert A. Simon en 1955[14] dans le cadre des études de la taille des villes et d'autres phénomènes. Il a été appliqué à la croissance des réseaux par Derek de Solla Price , en 1976[15], lorsqu'il s'intéressa aux réseaux de citations entre articles scientifiques. Le nom d' "attachement préférentiel" et la popularité des modèles de réseau sans-échelle provient des travaux de Albert-László Barabási et Réka Albert, qui ont redécouvert le processus de manière indépendante en 1999 pour l'appliquer à la distribution des degrés des liens entre les pages sur le web[16].
Articles connexes
Références
- Réka Albert et Albert-László Barabási, « Statistical mechanics of complex networks », Reviews of Modern Physics, vol. 74, no 1, , p. 47–97 (ISSN 0034-6861, DOI 10.1103/RevModPhys.74.47, Bibcode 2002RvMP...74...47A)
- Réka Albert et Albert-László Barabási, « Statistical mechanics of complex networks », Reviews of Modern Physics, vol. 74, , p. 47–97 (DOI 10.1103/RevModPhys.74.47, Bibcode 2002RvMP...74...47A, arXiv cond-mat/0106096, lire en ligne)
- A. Korn, A. Schubert et A. Telcs, « Lobby index in networks », PhysicsA, vol. 388, , p. 2221–2226 (DOI 10.1016/j.physa.2009.02.013, Bibcode 2009PhyA..388.2221K, arXiv 0809.0514)
- Reuven Cohen et Shlomo Havlin, « Scale-Free Networks Are Ultrasmall », Physical Review Letters, vol. 90, no 5, , p. 058701 (ISSN 0031-9007, PMID 12633404, DOI 10.1103/PhysRevLett.90.058701)
- Babak Fotouhi et Michael Rabbat, « Degree correlation in scale-free graphs », The European Physical Journal B, vol. 86, no 12, , p. 510 (DOI 10.1140/epjb/e2013-40920-6, Bibcode 2013EPJB...86..510F, arXiv 1308.5169, lire en ligne)
- K. Klemm et V. C. Eguíluz, « Growing scale-free networks with small-world behavior », Physical Review E, vol. 65, no 5, (DOI 10.1103/PhysRevE.65.057102, Bibcode 2002PhRvE..65e7102K, arXiv cond-mat/0107607)
- http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.176.6988
- (en) Holyst, Janusz A., Mean-field theory for clustering coefficients in Barabasi-Albert networks, (DOI 10.1103/PhysRevE.68.046126, lire en ligne).
- S.N. Dorogovtsev, A.V. Goltsev et J.F.F. Mendes, « Pseudofractal scale-free web », Physical Review E, vol. 65, , p. 066122 (DOI 10.1103/PhysRevE.65.066122, Bibcode 2002PhRvE..65f6122D, arXiv cond-mat/0112143)
- I.J. Farkas, I. Derényi, A.-L. Barabási et T. Vicsek, « Spectra of "real-world" graphs: Beyond the semicircle law », Physical Review E, vol. 64, , p. 026704 (DOI 10.1103/PhysRevE.64.026704, Bibcode 2001PhRvE..64b6704F, arXiv cond-mat/0102335)
- M. K. Hassan, M. Z. Hassan and N. I. Pavel, “Dynamic scaling, data-collapseand Self-similarity in Barabasi-Albert networks” J. Phys. A: Math. Theor. 44 175101 (2011) https://dx.doi.org/10.1088/1751-8113/44/17/175101
- Erol Pekoz, A. Rollin et N. Ross, « Total variation and local limit error bounds for geometric approximation », Bernoulli, (lire en ligne)
- G. Udny Yule et G. Udny Yule, « A Mathematical Theory of Evolution Based on the Conclusions of Dr. J. C. Willis, F.R.S », Journal of the Royal Statistical Society, vol. 88, no 3, , p. 433–436 (DOI 10.2307/2341419, JSTOR 2341419)
- Herbert A. Simon, « On a Class of Skew Distribution Functions », Biometrika, vol. 42, nos 3–4, , p. 425–440 (DOI 10.1093/biomet/42.3-4.425)
- D.J. de Solla Price, « A general theory of bibliometric and other cumulative advantage processes », Journal of the American Society for Information Science, vol. 27, no 5, , p. 292–306 (DOI 10.1002/asi.4630270505)
- Albert-László Barabási et Réka Albert, « Emergence of scaling in random networks », Science, vol. 286, no 5439, , p. 509–512 (PMID 10521342, DOI 10.1126/science.286.5439.509, Bibcode 1999Sci...286..509B, arXiv cond-mat/9910332, lire en ligne)
Liens externes
- "Cet Homme Pourrait gouverner le Monde"
- "Génération de Barabási–Albert Graphiques de Modèle de Code"
- Portail de l'informatique théorique