Modèle de Janssen

On considère un cylindre de rayon ${\displaystyle R}$ rempli de grains sur une hauteur ${\displaystyle H}$. La première hypothèse est de considérer le milieu granulaire comme un milieu continu de masse volumique ${\displaystyle \rho }$. Ensuite il vient 2 autres hypothèses :

1. Une contrainte verticale ${\displaystyle p_{z}}$ engendre une contrainte horizontale ${\displaystyle p_{r}}$ qui lui est directement proportionnelle : ${\displaystyle p_{r}=Kp_{z}}$. Le coefficient de Janssen ${\displaystyle K}$ prend en charge l'effet des voûtes qui se forment à l'intérieur du milieu granulaire. Notons qu'on aurait ${\displaystyle K=1}$ si la pression était isotrope, comme c'est le cas par exemple pour un fluide
2. Contre la paroi nous sommes à la limite de l’équilibre, soit en notant ${\displaystyle \mu _{s}}$ le coefficient de frottement, nous avons la relation entre les réactions normale et tangentielle : ${\displaystyle T=\mu _{s}N}$

Bilan des forces

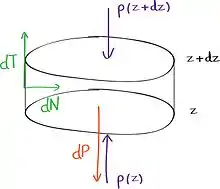
Considérons une petite tranche de silo de hauteur ${\displaystyle dz}$ (surface ${\displaystyle S=\pi R^{2}}$ et surface latérale ${\displaystyle dS_{l}=2\pi Rdz}$). En projection sur ${\displaystyle {\vec {e}}_{z}}$, l'équilibre s'écrit :

${\displaystyle dT-dP+p_{z}(z)S-p_{z}(z+dz)S=0}$

La 3^e loi de Newton donne : ${\displaystyle dN=p_{r}(z)dS_{l}}$

On en déduit donc avec les 2 hypothèses de Janssen : ${\displaystyle dT=\mu _{s}Kp_{z}(z)dS_{l}}$. En injectant ce résultat dans l'équation d'équilibre et en y ajoutant l'expression du poids ${\displaystyle dP=\rho gSdz}$ nous avons :

${\displaystyle \mu _{s}Kp_{z}(z)dS_{l}-\rho gSdz-{\frac {dp}{dz}}dzS=0}$

En simplifiant par ${\displaystyle Sdz}$ nous obtenons finalement l'équation différentielle vérifiée par la contrainte verticale :

${\displaystyle {\frac {dp_{z}}{dz}}-{\frac {p_{z}}{\lambda }}=-\rho g}$

Avec la longueur caractéristique : ${\displaystyle \lambda ={\frac {R}{2K\mu _{s}}}}$

La contrainte verticale ${\displaystyle p_{z}}$ vérifie une équation différentielle linéaire du premier ordre que l'on résout aisément avec la condition en haut de l'empilement : ${\displaystyle p_{z}(H)=0}$ :

${\displaystyle p_{z}(z)=\lambda \rho g(1-e^{-{\frac {H-z}{\lambda }}})}$

Un tel profil signifie que la pression dans le silo sature. En effet, à une hauteur ${\displaystyle z}$ fixée si l'on fait tendre ${\displaystyle H{\xrightarrow {}}\infty }$ c'est-à-dire lorsque l'on remplit indéfiniment le silo, la contrainte sature ${\displaystyle p_{z}{\xrightarrow {}}\lambda \rho g}$. En reprenant la 1^re hypothèse de Janssen, on comprend ce qu'il se passe physiquement : lorsque l'on verse une masse de grain, une partie se répercute verticalement et l'autre latéralement (effet de "voûtes") et c'est cette dernière qui est responsable de l'éclatement des silos. Souvent la partie latérale du silo, contrairement au fond, n'est pas fabriquée pour résister à des charges importantes.

Reprenons l'expression de la contrainte verticale, mais cette fois-ci au fond du silo :

${\displaystyle p_{z}(0)=\lambda \rho g(1-e^{-{\frac {H}{\lambda }}})}$

Si l'on désire la masse apparente au fond du silo, celle-ci s'exprime comme ${\displaystyle m_{app}={\frac {p_{z}(0)S}{g}}}$ soit :

${\displaystyle m_{app}=\lambda \rho S(1-e^{-{\frac {H}{\lambda }}})}$

Saturation de la masse apparente

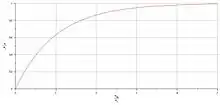
En notant ${\displaystyle m_{c}=\lambda \rho S}$ la masse critique et en remarquant que la masse théorique versée s'exprime comme ${\displaystyle m_{th}=H\rho S}$, on obtient l'expression de la masse apparente en fond de silo en fonction de la masse théoriquement versée dans celui-ci :

${\displaystyle m_{app}=m_{c}(1-e^{-{\frac {m_{th}}{m_{c}}}})}$

Physiquement, ce résultat signifie que même si l'on remplit indéfiniment le silo, la masse que l'on mesurerait au fond ne dépasserait pas la masse critique ${\displaystyle m_{c}}$. Dans un souci de conservation de la masse, on comprend bien que si l'on ne retrouve pas la masse versée au fond du tube c'est qu'une partie de celle-ci est absorbée par la partie latérale du silo.

Formation de voûtes

Dans cette partie nous allons étudier des cas limites. Pour plus de simplicité, nous notons ${\displaystyle \delta =H-z}$ la profondeur dans l'empilement. La pression dans celui-ci vaut donc en fonction de la profondeur :

${\displaystyle p_{z}(\delta )=\lambda \rho g(1-e^{-{\frac {\delta }{\lambda }}})}$

Lorsque ${\displaystyle \delta \ll \lambda }$ (faibles profondeurs) : ${\displaystyle p_{z}(\delta )\approx \rho g\delta }$ autrement dit la masse apparente est proche de la masse versée, les zones inférieures subissent classiquement le poids des zones supérieures.

Lorsque ${\displaystyle \delta \gg \lambda }$ (grandes profondeurs) : ${\displaystyle p_{z}(\delta )\approx \lambda \rho g}$ autrement dit la masse apparente est proche de la masse critique, les zones inférieures ne subissent plus le poids des zones supérieures.

En conséquence, on donne un sens physique à la longueur ${\displaystyle \lambda }$ : elle caractérise la position (en profondeur) des voûtes. Au-dessus de celles-ci on subit le poids de la colonne de grains alors qu'en dessous on en est protégé.

• Matériau granulaire
• Cohésion des grains de sable
• Angle de talus naturel
• Silo (stockage)

• Portail de la physique