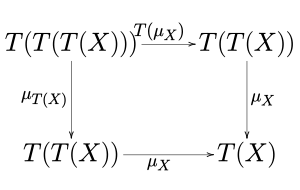Monade (théorie des catégories)

La notion apparaît pour la première fois, sous le nom de « construction standard », dans un article de Roger Godement publié en 1958[1]. Il s'agissait en fait d'une comonade, qui permettait de résoudre un problème de cohomologie des faisceaux. La notion est reprise pour l'étude de l'homotopie des catégories par Peter Huber[2], qui donne notamment la preuve que toute paire d'adjoint donne lieu à une monade. En 1965, Heinrich Kleisli (en)[3] et indépendamment, Samuel Eilenberg et John Coleman Moore[4] démontrent la réciproque. Ce sont ces derniers qui donnent le nom de « triples » à la construction.

En 1963, William Lawvere propose une théorie catégorique de l'algèbre universelle. Fred Linton montre en 1966 que cette théorie peut s'exprimer en termes de monades[5]. Les monades, issues de considérations plutôt topologiques, et a priori plus difficiles à manier que les théories de Lawvere, sont devenues la formulation la plus courante de l'algèbre universelle en termes de catégories.

En 1966, Jean Bénabou propose le nom de monade lors d'une conférence. Évoquant le mot « monoide », voire « monoidal triad » en anglais, ce nom est popularisé par Saunders Mac Lane dans son livre Categories for the Working Mathematician (1971). Le lien initial avec la philosophie de Leibniz (où la monade peut être décrite comme une unité génératrice de l'univers) n'est pas avéré[6]^,[7]^,[8].

Dans les années 1980, Eugenio Moggi (en) utilise les monades en informatique théorique pour modéliser certains aspects des programmes informatiques, tels que la gestion d'exceptions ou les effets de bord[9]. Cette idée sera prise au sérieux dans l'implémentation de plusieurs langages de programmation fonctionnelle sous la forme de primitives appelées également « monades ».

En 2001, plusieurs mathématiciens réalisent le lien entre cette utilisation des monades pour étudier la sémantique dénotationelle d'un programme et les travaux de Lawvere[10], un lien entre algèbre et sémantique qui constitue aujourd'hui un domaine de recherche actif.

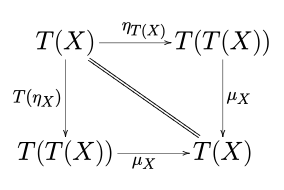
Une monade est la donnée d'un triplet ${\displaystyle (T,\eta ,\mu )}$ avec :

• ${\displaystyle T}$ un endo-foncteur d'une catégorie ${\displaystyle T:{\mathcal {C}}\to {\mathcal {C}}}$ ;
• ${\displaystyle \eta }$ une transformation naturelle ${\displaystyle \eta :1_{\mathcal {C}}\to T}$ avec ${\displaystyle 1_{\mathcal {C}}}$ le foncteur identité de ${\displaystyle {\mathcal {C}}}$ ;
• ${\displaystyle \mu }$ une transformation naturelle ${\displaystyle \mu :T\circ T\to T}$ ;

et telle que les diagrammes suivants commutent :

C'est-à-dire ${\displaystyle \mu \circ T\mu =\mu \circ \mu T}$ (qui mime l'associativité d'un monoïde) et ${\displaystyle \mu \circ T\eta =\mu \circ \eta T=1_{T}}$ (existence d'un élément neutre).

Soit une paire d'adjoints ${\displaystyle F\dashv G}$, ayant pour unité

${\displaystyle \eta$ :{\mathsf {id}}\mapsto G\circ F}

et co-unité

${\displaystyle \varepsilon :F\circ G\mapsto {\mathsf {id}}}$

Alors le foncteur ${\displaystyle T=G\circ F}$, muni des transformations

${\displaystyle \eta$ :{\mathsf {id}}\mapsto T}

${\displaystyle \mu =G(\varepsilon F):T\circ T\mapsto T}$

forme une monade.

Réciproquement, pour toute monade ${\displaystyle (T,\eta ,\mu )}$, il existe une paire d'adjoints ${\displaystyle F\dashv G}$ telle que ${\displaystyle T=G\circ F}$. Il existe potentiellement de nombreuses décompositions, la plus petite formant la catégorie de Kleisli, la plus large la catégorie d'Eilenberg-Moore.

• Michael Barr (en), Charles Wells (en), Toposes, triples and theories
• Carson Berger, On some aspects of the theory of monads
• Martin Hyland, John Power, The Category Theoretic Understanding of Universal Algebra: Lawvere Theories and Monads
• Saunders Mac Lane, Categories for the Working Mathematician

• Portail des mathématiques