Mouvements de Reidemeister
En mathématiques, et plus précisément en théorie des nœuds, les mouvements de Reidemeister sont des mouvements locaux de brins d'un nœud dans diagrammes de nœuds. Kurt Reidemeister, en 1927, et, indépendamment, Alexander Briggs en 1926, ont démontré que deux diagrammes de nœuds représentent le même nœud, si on peut passer de l'un à l'autre par une suite de mouvements de Reidemeister.
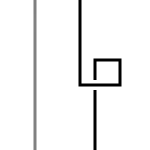
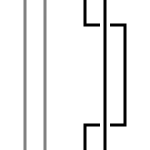

Description des mouvements
Il y en a trois types de mouvements comme montrés sur la figure à droite. On numérote le type de mouvement selon le nombre de morceaux de brins qui y apparaît. Le mouvement de type 1 enroule ou déroule le brin. Le type 2 superpose/sépare un morceau du brin sur l'autre. Le mouvement de type 3 déplace un morceau de brin sur un croisement.
Le mouvement de type 1 est le seul qui affecte l'entortillement. Le mouvement de type 3 est le seul qui ne change pas le nombre de croisements.
Exécution des mouvements
Trace (1983) a démontré que l'on peut passer d'un diagramme à un autre avec des mouvements de type II et III si et seulement si ils représentent le même nœud, ont le même entortillement et le même indice. De plus, les travaux de Östlund (2001), Manturov (2004), et Hagge (2006) montre que pour chaque nœud, il existe une paire de diagrammes où il faut utiliser les trois types de mouvements pour passer de l'un à l'autre. Alexander Coward a démontré que pour passer d'un diagramme à un autre représentant le même nœud, il existe une séquence de mouvements ordonnés par type : d'abord des mouvements de type I, puis de type II, puis de type III, puis de type II à nouveau. Les mouvements avant le type III augmente le nombre de croisements alors que ceux après diminue le nombre de croisements.
Nombre de mouvements
Coward & Lackenby (2014) ont démontré que le nombre de mouvements pour passer d'un diagramme à un autre du même nœuds est borné par une tour d'exponentielles (en le nombre de croisements). Plus précisément, si n est la somme du nombre de croisements dans les deux diagrammes, alors la borne supérieure est où la hauteur de 2 est .
Lackenby (2015) a montré que le nombre de mouvements pour passer d'un diagramme du non-nœud au diagramme standard du non-nœud est borné par un polynôme en le nombre de croisements. Plus précisément, s'il y a c croisements, la borne supérieure est .
Hayashi (2005) a donné une borne supérieure, qui dépend du nombre de croisements, pour le nombre de mouvements de Reidemeister nécessaires pour dénouer un entrelac.
Bibliographie
- Alexander, James W.; Briggs, G. B. (1926), "On types of knotted curves", Ann. of Math., 28: 562–586, doi:10.2307/1968399, MR 1502807
- Coward, Alexander; Lackenby, Marc (2014), "An upper bound on Reidemeister moves", American Journal of Mathematics, 136 (4): 1023–1066, doi:10.1353/ajm.2014.0027, MR 3245186
- Galatolo, Stefano (1999), "On a problem in effective knot theory", Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl., 9 (4): 299–306, MR 1722788
- Hagge, Tobias (2006), "Every Reidemeister move is needed for each knot type", Proc. Amer. Math. Soc., 134 (1): 295–301, doi:10.1090/S0002-9939-05-07935-9, MR 2170571
- Hass, Joel; Lagarias, Jeffrey C. (2001), "The number of Reidemeister moves needed for unknotting", Journal of the American Mathematical Society, 14 (2): 399–428, doi:10.1090/S0894-0347-01-00358-7, MR 1815217
- Hayashi, Chuichiro (2005), "The number of Reidemeister moves for splitting a link", Math. Ann., 332 (2): 239–252, doi:10.1007/s00208-004-0599-x, MR 2178061
- Lackenby, Marc (2015), "A polynomial upper bound on Reidemeister moves", Annals of Mathematics, Second Series, 182 (2): 491–564, arXiv:1302.0180 Freely accessible, doi:10.4007/annals.2015.182.2.3, MR 3418524
- Manturov, Vassily Olegovich (2004), Knot theory, Boca Raton, FL: Chapman & Hall/CRC, doi:10.1201/9780203402849, (ISBN 0-415-31001-6), MR 2068425
- Östlund, Olof-Petter (2001), "Invariants of knot diagrams and relations among Reidemeister moves", J. Knot Theory Ramifications, 10 (8): 1215–1227, doi:10.1142/S0218216501001402, MR 1871226
- Reidemeister, Kurt (1927), "Elementare Begründung der Knotentheorie", Abh. Math. Sem. Univ. Hamburg, 5 (1): 24–32, doi:10.1007/BF02952507, MR 3069462
- Trace, Bruce (1983), "On the Reidemeister moves of a classical knot", Proc. Amer. Math. Soc., 89 (4): 722–724, doi:10.2307/2044613, MR 0719004
- Portail des mathématiques