Nœud plat (mathématiques)
En théorie des nœuds, le nœud plat ou nœud carré, est un nœud composé obtenu comme somme connexe du nœud de trèfle et de son image par une réflexion. Il est lié au nœud de vache qui est, lui, la somme connexe de deux nœuds de trèfle identiques. Le nœud de trèfle étant le nœud non trivial le plus simple, le nœud plat et le nœud de vache sont les plus simples des nœuds composés.

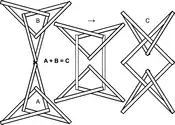
Le nœud plat mathématique est la version mathématique du nœud plat commun ; il est obtenu à partir de celui-ci en reliant les bouts libres.
Construction
Le nœud plat est construit à partir de deux nœuds de trèfle, l’un dextre et l’autre senestre. Chacun des nœuds est sectionné, et les extrémités libres sont assemblées deux à deux. La somme qui en résulte est le nœud plat.
Il est important que les nœuds de trèfle d'origine soient images miroir l'une de l'autre. Si deux nœuds de trèfles identiques sont utilisés, le résultat est un nœud de vache.
Une courbe paramétrée simple suivant un nœud plat est donnée par les formules .
 Nœud plat obtenu par les formules précédentes
Nœud plat obtenu par les formules précédentes Nœud de vache
Nœud de vache
Propriétés
Le nœud plat est achiral, ce qui signifie qu’il est différent de son image miroir.
Son nombre de croisements est 6, ce qui correspond au plus petit nombre possible de croisements pour un nœud composé.
Son polynôme d’Alexander est
soit le carré du polynôme d’Alexander du nœud de trèfle. De même, le polynôme d’Alexander-Conway du nœud plat est
Ces deux polynômes sont les mêmes que ceux du nœud de vache. Par contre, le polynôme de Jones du nœud plat est
C'est le produit des polynômes de Jones des nœuds de trèfle dextre et senestre ; il est donc différent de celui du nœud de vache.
Le groupe de nœud du nœud plat est défini par les relations :
Il est isomorphe au groupe de nœud du nœud de vache, ce qui constitue l'exemple le plus simple de deux nœuds différents dont les groupes de nœud sont isomorphes.
Contrairement au nœud de vache, le nœud plat est un nœud ruban (en) et est donc aussi un nœud bordant .

Lien externe
Noeud plat et noeud de vache, dans MathCurve, illustrant le lien entre le nœud plat commun et le nœud plat mathématique.
Références
- Portail des mathématiques