Nombre chanceux
En mathématiques, un nombre chanceux est un entier naturel dans un ensemble qui est généré par un « crible » similaire au crible d'Ératosthène qui génère les nombres premiers[1],[2],[3].
| On commence avec la suite d'entiers démarrant par 1 : | ||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Puis on enlève un nombre sur deux, ce qui ne laisse que les entiers impairs : | ||||||||||||||||||||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | ||||||||||||
| Le deuxième terme de la suite est désormais 3. Ensuite, on enlève un nombre sur trois parmi ceux qui restent dans la liste : | ||||||||||||||||||||||||
| 1 | 3 | 7 | 9 | 13 | 15 | 19 | 21 | 25 | ||||||||||||||||
| Le troisième nombre survivant est 7. On enlève alors un nombre sur sept parmi ceux qui restent dans la liste : | ||||||||||||||||||||||||
| 1 | 3 | 7 | 9 | 13 | 15 | 21 | 25 | |||||||||||||||||
Ne doit pas être confondu avec nombre chanceux d'Euler.
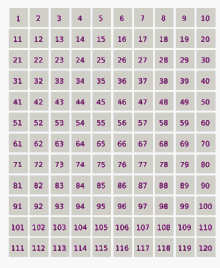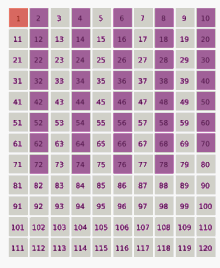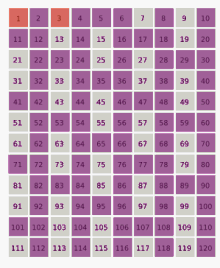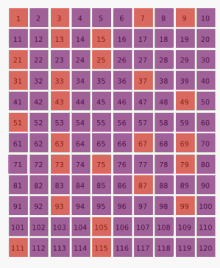
Le quatrième nombre survivant est 9. Puis on enlève un nombre sur neuf parmi ceux qui restent dans la liste, etc.
Si l'on répète cette procédure indéfiniment, les survivants sont les nombres chanceux (suite A000959 de l'OEIS) :
1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, …
Le terme fut introduit en 1956 dans un article par Gardiner, Lazarus, Metropolis et Ulam[4]. Ils les nommèrent « chanceux » à cause de leur lien avec l'histoire du problème de Josèphe, contée par le chroniqueur Flavius Josèphe.
Il existe une infinité de nombres chanceux. Ils partagent certaines propriétés avec les nombres premiers, tel que le comportement asymptotique en accord avec le théorème des nombres premiers ; la conjecture de Goldbach a été étendue à eux. Les nombres chanceux jumeaux et les nombres premiers jumeaux semblent aussi apparaître avec une fréquence similaire.[réf. souhaitée]
Nombres premiers chanceux
Un nombre premier chanceux est un nombre qui est à la fois premier et chanceux.
On ignore s'il existe aussi une infinité de nombres premiers chanceux. Les vingt premiers sont (suite A031157 de l'OEIS) : 3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193, 211, 223, 241, 283, 307, 331, 349.
Autres cribles similaires
Un autre crible imaginé par Ulam et ses compères[4], semblable mais donnant des résultats différents, est celui qu'ils ont appelé "crible de Flavius Josèphe".
Un troisième crible du même type est celui dit de Tchoukaillon, voir la suite A007952 de l'OEIS, et un quatrième est celui donnant les nombres pseudo-chanceux, voir la suite A249876 de l'OEIS.
Notes et références
- (en) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « Lucky number » (voir la liste des auteurs) et « Lucky prime » (voir la liste des auteurs).
- Cet article est partiellement ou en totalité issu de l'article intitulé « Nombre premier chanceux » (voir la liste des auteurs).
- (en) Ivars Peterson (en), « MathTrek: Martin Gardner's Lucky Number », sur www.sciencenews.org.
- (en) Eric W. Weisstein, « Lucky Number », sur MathWorld.
- Attention: ce crible bien que "similaire" à celui d'Eratosthène , donne un résultat très différent qui, notamment, exclut certains entiers premiers (ex: 5), et inclut des nombres composés (ex:21)
- (en) Verna Gardiner, R. Lazarus, N. Metropolis et S. Ulam, « On certain sequences of integers defined by sieves », Mathematics Magazine, vol. 29, no 3, , p. 117-122 (DOI 10.2307/3029719, zbMATH 0071.27002).
- Arithmétique et théorie des nombres