Nombre de Dottie

Le nombre de Dottie est un nombre remarquable, défini comme l'unique solution de l'équation x - cos(x)=0[alpha 1].

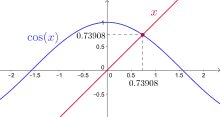
Représentation graphique du nombre de Dottie

Sa valeur approchée est 0,739085133215[alpha 2].

Sa représentation géométrique est le point d'intersection de la droite d'équation y = x et de la courbe d'équation y = cos (x).

On ne connaît pas actuellement d'application utilisant cette valeur, ni en algèbre, ni en géométrie, ni en sciences appliquées ; le professeur de mathématiques qui lui a donné son nom l'utilise uniquement comme source d'exercices pour ses étudiants[1].

Le nombre de Dottie est transcendant d'après le théorème d'Hermite-Lindemann[2]^,[alpha 3].

Valeurs trigonométriques liées à ce nombre

Appelons $D$ le nombre de Dottie, on a :

sin(D) \approx 0,673612029183

tan(D) \approx 0,911413312094

Bibliographie

James Stewart Single Variable Calculus : Concepts and Contexts Brook/Cole 2010, (ISBN 978-0-495-55972-6), page 314
Kaplan S.R. The Dottie Number Math.Mag. 80, 2007, pages 73 et 74
Miller T.H. On the Numerical Values of the Roots of the Equation cos x = x Proc. Edimburg Math. Soc. 9, 1890, pages 80 à 83
Bertrand J. Exercice III Traité d'Algèbre Vol 1-3, 4^e édition Paris Librairie de L. Hachette et C^ie, 1865, page 285

Notes et références

Notes

x est, naturellement, exprimé en radians.
Le site en russe de pikabu donne plus précisément comme valeur 0,739085 133215 160641 66... voir le lien http://pikabu.ru/story/kosinus_07390851332_1230436.
Une calculette d'ordinateur à 32 décimales donne le nombre 0,739085 133215 160641 655312 087673 87...
On note $D$ le nombre de Dottie. Supposons qu'il n'est pas transcendant. Il est donc algébrique et donc son produit par i aussi. De plus par définition, ${\mathtt {Re}}(e^{iD})=D$ . Mais alors d'après le théorème d'Hermite-Lindemann, on a $e^{iD}$ qui est transcendant. Or comme ${\mathtt {Re}}(e^{iD})^{2}+{\mathtt {Im}}(e^{iD})^{2}=1$ , ${\mathtt {Re}}(e^{iD})$ est transcendant aussi, et n'est donc pas algébrique : on aboutit à une contradiction si l'on suppose $D$ algébrique. $D$ est donc transcendant.

Références

Samuel R Kaplan, « The Dottie Number », Mathematics Magazine, vol. 80,‎ février 2007, p. 73 (lire en ligne, consulté le 29 novembre 2017)
(en) Eric W. Weisstein, « Dottie Number », sur MathWorld

Liens externes

Jérôme Cottanceau, « Les nombres magiques », sur Chou romanesco, vache qui rit et intégrales curvilignes, 27 septembre 2008

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] x est, naturellement, exprimé en radians.

[2] Le site en russe de pikabu donne plus précisément comme valeur 0,739085 133215 160641 66... voir le lien http://pikabu.ru/story/kosinus_07390851332_1230436.
Une calculette d'ordinateur à 32 décimales donne le nombre 0,739085 133215 160641 655312 087673 87...

[5] On note $D$ le nombre de Dottie. Supposons qu'il n'est pas transcendant. Il est donc algébrique et donc son produit par i aussi. De plus par définition, ${\mathtt {Re}}(e^{iD})=D$ . Mais alors d'après le théorème d'Hermite-Lindemann, on a $e^{iD}$ qui est transcendant. Or comme ${\mathtt {Re}}(e^{iD})^{2}+{\mathtt {Im}}(e^{iD})^{2}=1$ , ${\mathtt {Re}}(e^{iD})$ est transcendant aussi, et n'est donc pas algébrique : on aboutit à une contradiction si l'on suppose $D$ algébrique. $D$ est donc transcendant.

[Kaplan-3] Samuel R Kaplan, « The Dottie Number », Mathematics Magazine, vol. 80,‎ février 2007, p. 73 (lire en ligne, consulté le 29 novembre 2017)

[4] (en) Eric W. Weisstein, « Dottie Number », sur MathWorld