Calculateur analogique

Un calculateur analogique est une application particulière des méthodes analogiques consistant à remplacer l'étude d'un système physique donné par celle d'un autre système physique régi par les mêmes équations. Pour que cela présente un intérêt, le système « analogue » doit être facile à construire, les mesures aisées et moins coûteuses que sur le système réel.

L'Elwat, un calculateur analogique polonais fabriqué entre 1967 et 1969 ; les éléments visibles sont, de gauche à droite, un voltmètre, un téléscripteur, un oscilloscope et l'ordinateur à proprement parler.

Un calculateur analogique proprement dit est constitué d'un ensemble de modules électroniques (et/ou électromécaniques) interconnectés pour modéliser un problème à résoudre. Les connexions sont assurées par un panneau de câblage amovible facilitant les changements de problèmes. Les résultats (mesure des tensions électriques représentant les différentes variables) sont le plus souvent enregistrés sous forme de courbes en fonction du temps. Ce concept contraste avec celui des calculateurs numériques, qui par nature travaillent uniquement sur des quantités discrètes, ne manipulent que des nombres et effectuent séquentiellement leurs calculs, alors que le calculateur analogique travaille sur des variables continues, toutes les opérations étant effectuées en parallèle.

Les calculateurs analogiques, dévolus à la résolution des systèmes d'équations différentielles, sont aujourd'hui tombés en désuétude face à la puissance et à l'universalité des calculateurs numériques. Mais pour certaines fonctions et dans certaines conditions d'emploi, certains calculateurs mécaniques ou analogiques continuent à être développés. Par exemple l'AREE (développé par les américains pour les environnements sévères de sondes et robots pour l'exploration de planètes à l'environnement hostile)^{[réf. nécessaire]}.

Historique

Calculateur analogique électronique des Ets Boeing (1953), exposé au Musée d'Histoire et de l’Industrie de Seattle.

Sans remonter aux règles à calcul, les calculateurs analogiques ont été développés à partir des travaux d'un physicien britannique, Lord Kelvin, qui a inventé un marégraphe mécanique[1] dans les années 1870. D'autres systèmes furent mis au point entre les deux guerres mondiales : calculateurs de tir pour l'artillerie, analyseurs harmoniques pour l'ingénierie, cuves rhéographiques pour la mécanique des fluides, régulateurs industriels. À partir des années 1940 ont été développés et industrialisés de nombreux calculateurs analogiques électroniques. Plus tard des calculateurs à bain d'huile ont été inventés, la grandeur d'entrée étant le courant et la grandeur intégrée étant la température (ces calculateurs ont permis de définir les commandes de vol du Concorde par exemple). Des systèmes de régulation périphériques compensaient les pertes thermiques. Ainsi si nous substituons la variable vitesse V à la variable courant I et si nous substituons la variable distance D à la variable température T, nous pouvons « calculer » la distance en mesurant la température T d'un bain d'huile chauffé par un courant I proportionnel à V.

Les calculateurs analogiques électroniques « universels » se sont développés à partir des années 1950, essentiellement grâce à la mise au point de l'amplificateur opérationnel (amplificateur dit « à courant continu », car sa bande passante n'a pas de limite inférieure). Une tentative antérieure pour éviter la difficulté de réalisation de tels amplificateurs a été d'utiliser l'amplitude d'un signal porteur « haute fréquence » comme support d'information (calculateur Analac du groupe CSF). En France, le calculateur Djinn type 20 AS (fabriqué par le laboratoire Derveaux) comportait une vingtaine d'amplificateurs opérationnels. Il permettait de résoudre un système de quelques équations différentielles[2]. La société SEA fabriquait le OME P2 sensiblement équivalent. Les véritables calculateurs analogiques utilisables de façon industrielle sont venus du constructeur américain « Electronics Associates Inc. » avec le 231R à tubes électroniques[3] dont la précision atteignait 10^-4 et permettait de résoudre un problème d'une trentaine d'équations différentielles. Il disposait d'un panneau d'interconnexion amovible permettant de passer (presque) rapidement d'un problème à un autre. En 1965, le même constructeur sortait le calculateur 8800 qui, outre sa capacité plus que doublée en nombre d'opérateurs et le remplacement des tubes électroniques par des transistors, permettait d'effectuer les calculs beaucoup plus rapidement, et surtout, avait la possibilité d'être couplé avec un calculateur numérique, créant ainsi un calculateur hybride[4].

Deux options étaient proposées par ce constructeur : un calculateur « 16 bits » de puissance limitée dont le seul rôle était d'automatiser le calculateur analogique (réglage des coefficients, vérification des interconnexions entre opérateurs), ou bien un calculateur « temps réel » « 32 bits » très rapide de sa propre fabrication prenant part aux calculs et échangeant des données en temps réel via des convertisseurs analogues-digitaux et digitaux-analogiques (calculateur numérique EAI 8400, l'ensemble hybride prenant la référence EAI 8900). Les ultimes perfectionnements des années 1970 ont consisté à remplacer les derniers composants électro-mécaniques par des composants électroniques (chopper des amplificateurs opérationnels, réglage des coefficients).

À partir de 1980, le développement fulgurant des calculateurs numériques, et en particulier de leur vitesse de calcul, leur a permis d'effectuer des calculs en temps réel, ce qui n'était accessible auparavant qu'aux calculateurs analogiques, et de traiter des problèmes de plus en plus complexes, les calculs étant effectués séquentiellement, alors qu'un calculateur analogique effectuant toutes les opérations en parallèle était limité par la complexité des problèmes à traiter. À partir de cette époque, l'intérêt des grands calculateurs analogiques a disparu, et progressivement, le calcul analogique et hybride n'a subsisté que dans des circuits électroniques dédiés à des applications particulières : régulations, asservissements, ou en tant que liaisons facilement reconfigurables entre des équipements physiques et les processeurs numériques. Ce déclin a été accéléré par le développement des logiciels permettant de modéliser facilement les systèmes physiques tel que Matlab et dont un des ancêtres était le CSMP (Continuous System Modelling Program introduit par IBM), permettant de résoudre facilement un système d'équations différentielles.

Cependant, après plusieurs décennies de déclin face au numérique, cette technologie voit un regain d’intérêt en montrant son efficacité face aux super-calculateurs dans le cas de calculs précis[5].

Domaines d'applications

Les calculateurs analogiques sont (ou plus exactement étaient) très bien adaptés à la résolution des systèmes d'équations différentielles ordinaires (c.-à-d. à une seule variable) grâce à leurs intégrateurs qui effectuent une vraie intégration en fonction du temps. Bien qu'ils puissent traiter des problèmes où la variable indépendante ne soit pas le temps, ils ont principalement été utilisés dans les deux domaines suivants :

Calculs d'études des systèmes pour lesquels le comportement dynamique est essentiel : régulations des procédés industriels (usines chimiques, centrales nucléaires ou classiques), pilotage et guidage en aéronautique, astronautique, systèmes d'armes, études théoriques (stabilité des plasmas, chambres à bulles). Dans ce cas, le temps "calcul" peut différer du temps physique : souvent accéléré de façon à obtenir une grande productivité (plusieurs centaines de milliers d'atterrissages pour la certification des pilotes automatiques de Concorde et Airbus), quelquefois ralenti pour observer confortablement et en détail le comportement de phénomènes rapides (trajectoires d'électrons).
Simulateurs en temps réel, dans lesquels sont intégrés des équipements physiques, et même un opérateur humain, comme dans les grands projets astronautiques.

Les composants d'un calculateur analogique

L'élément de base : l'amplificateur opérationnel

Associé à des éléments passifs linéaires ou non, l'amplificateur opérationnel est le cœur des opérateurs, c'est-à-dire des modules de calculs tels que les sommateurs, les intégrateurs, les multiplieurs.

Les principales propriétés des amplificateurs opérationnels sont les suivantes :

bande passante non limitée dans les fréquences basses (ils sont quelquefois improprement appelés « amplificateurs à courant continu ») ;
gain extrêmement élevé et très faible tension d'offset si bien que la tension d'entrée est toujours très voisine de zéro ;
inversion entre entrée et sortie : $Es=-|Gain|*e$ ;
grande impédance d'entrée ;
courant d'entrée négligeable.

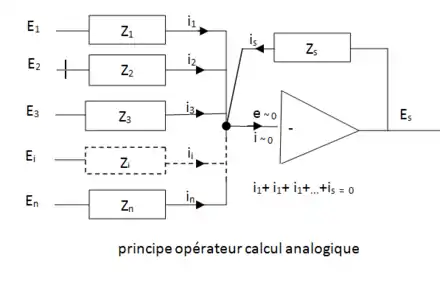
En négligeant le courant d'entrée i, la loi de Kirchhoff appliquée au point d'entrée de l'amplificateur donne :

i1+i2+i3+...+in+is=0

, soit

is=-(i1+i2+i3+...+in)

La tension d'entrée e étant négligeable par rapport aux tensions E1, E2, ... Es on peut écrire symboliquement :

Es=-(E1*{\frac {Zs}{Z1}}+E2*{\frac {Zs}{Z2}}+E3*{\frac {Zs}{Z3}}+...+En*{\frac {Zs}{Zn}})

Il y a toujours inversion de signe entre entrées et sortie en raison du montage de l'impédance Zs en « contre réaction ».

Sommateur et inverseur

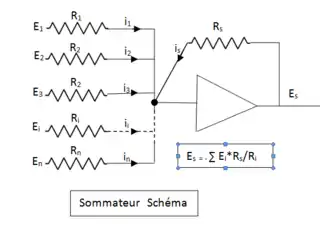
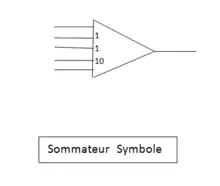
L'objectif de ce module est d'effectuer la somme de plusieurs tensions. Les impédances d'entrée et de contre-réaction sont toutes des résistances. Dans la pratique le rapport Rs/Ri = 1 ou 10, ce qui correspond à un gain de 1 ou 10 selon les entrées utilisées (voir la représentation symbolique du sommateur). Il est à noter que la précision de l'opération dépend directement de la qualité de l'amplificateur opérationnel (courant d'entrée et tension d'offset négligeable) et de la précision de chacune des résistances. (erreur inférieure à $10^{-4}$ sur les calculateurs « haut de gamme »). Pour obtenir une telle précision, les résistances sont du type « bobiné » (bobinage double en sens inverse pour minimiser l'effet d'inductance qui nuirait à la précision dynamique du sommateur). Les valeurs de résistances communément utilisées sont de 100 kΩ et 1 MΩ pour les calculateurs ayant une référence de 100 volts, ou de 10 kΩ et 100 kΩ pour une référence de 10 volts.

Le signal de sortie est inversé par rapport aux signaux d'entrée. Les équations à résoudre pouvant comporter des termes positifs ou négatifs, un calculateur analogique comporte également des « inverseurs » Es = - Ee qui sont simplement des sommateurs avec une seule résistance d'entrée.

Intégrateur-sommateur

L'objectif de ce module est de fournir une tension de sortie Es qui soit l'intégrale en fonction du temps de la somme des tensions appliquées aux entrées de l'intégrateur.

Comme pour le sommateur, le réseau d'entrée est un ensemble de résistances Ri, mais l'impédance de contre-réaction est un condensateur C.

On a : $is=-(i1+I2+...+In)$ avec $is=C*{\frac {dEs}{dt}}$ et $i1={\frac {E1}{R1}}$ , $i2={\frac {E2}{R2}}$ , ..., soit : $Es=-\int ({\frac {E1}{R1C}}+{\frac {E2}{R2C}}+...{\frac {En}{RnC}})dt$

Le réseau d'entrée est identique à celui d'un sommateur et la représentation symbolique des entrées est également affectée du facteur 1 ou 10 . Sur les calculateurs « haut de gamme » les intégrateurs disposent d'un choix de capacité variant d'un facteur de 10 en 10 depuis 0,1 nF jusqu'à 10 μF, ce qui donne des constantes de temps RC pouvant varier de $10^{-5}$ à $10$ .

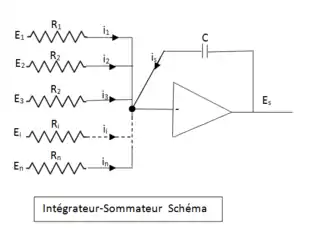
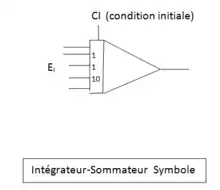
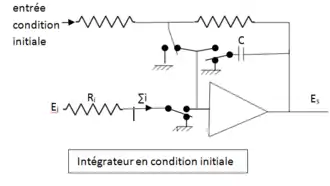
Un ensemble de commutateurs est associé à chaque intégrateur afin de définir un des trois états possibles des intégrateurs :

L'état initial : rien n'évolue on est figé au temps $t=0$ , l'intégrateur fonctionne alors comme un simple inverseur avec une entrée spéciale permettant de définir la valeur initiale de Es à laquelle est chargée le condensateur (voir schéma : « intégrateur en condition initiale »)
L'état calcul : $Es$ évolue à partir de la condition initiale, en intégrant les signaux d'entrée (tous les commutateurs ont basculé)
L'état mémoire : à un moment quelconque du calcul, on fige le temps t (par exemple pour faire des mesures particulières ou des contrôles etc.). Pour cela, le réseau d'entrée est déconnecté ce qui entraine is = 0 et par suite ${\frac {d(Es)}{dt}}=0$ : plus rien n'évolue.

Coefficient

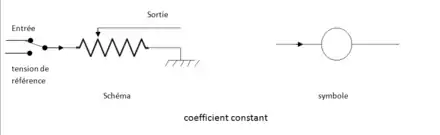
Cet élément effectue le produit d'une variable (la tension d'entrée) par une constante dont la valeur ne peut être comprise qu'entre zéro et un. Pour effectuer correctement le réglage, un commutateur remplace la tension d'entrée par la tension de référence et un voltmètre de précision est connecté sur le curseur. Technologiquement, il a d'abord été réalisé par un potentiomètre de précision multi-tour qui devait être réglé manuellement, puis sur les calculateurs haut de gamme chaque potentiomètre a été associé à un servomécanisme réglable à partir d'un clavier et dans les années 1970, il a été remplacé par un réseau de résistances commutés électroniquement (multiplieur hybride). Dans les calculateurs hybrides, le réglage des coefficients étaient télécommandés à partir du calculateur numérique.

Multiplieur

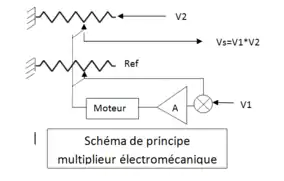
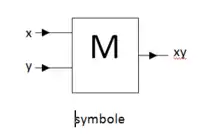
Le multiplieur effectue le produit de deux variables (les deux tensions électriques d'entrée V1 et V2). C'est typiquement une opération non linéaire, il n'y a pas de solution électronique simple pour l'implémenter avec précision. Il a d'abord été réalisé de façon électromécanique à l'aide de deux potentiomètres jumelés et d'un asservissement. Le premier potentiomètre est utilisé pour asservir la position des curseurs jumelés à la tension V1. La tension V2 est appliquée à l'entrée du second potentiomètre et on récupère le produit V1*V2 sur son curseur. L'inconvénient de ce dispositif est qu'il est dissymétrique, avec une bande passante très réduite pour l'entrée V1, qui doit entraîner tout un système mécanique.

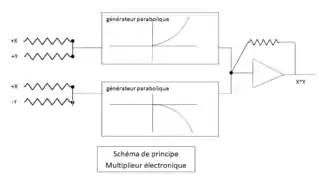
Par la suite,il a été remplacé par un système entièrement électronique qui réalise le produit par l'équation : $4x*y=(x+y)^{2}-(x-y)^{2}$ . Il nécessite deux générateurs de courant « paraboliques », un inverseur pour fournir -X et un amplificateur opérationnel pour fournir la tension de sortie résultat. Les générateurs paraboliques sont constitués d'un réseau de résistances et de diodes, dont les diodes se débloquent successivement en fonction de la tension d'entrée du réseau. Chaque parabole est donc approximée par une suite de segments, au moins une vingtaine de segments sont nécessaires pour obtenir une précision de l'ordre de $10^{-4}$ .

Diviseur

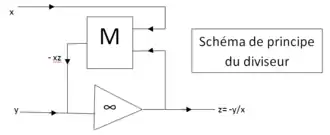
Le diviseur comporte les mêmes éléments que le multiplieur (potentiomètre asservi mécaniquement ou réseau de résistances et de diodes), mais ils sont montés en contre réaction de l'amplificateur opérationnel (et non en tant qu'élément d'entrée).

On a donc : $xz+y=0$ , soit : $z=-{\frac {y}{x}}$ .

Générateurs de fonctions non linéaires arbitraires

Les fonctions non linéaires sont approximées par une succession de segments de droites (de l'ordre de la dizaine). On réalise une impédance non linéaire à l'aide d'un réseau de potentiomètres de résistances et de diodes. Chaque segment nécessite deux éléments de réglage : un potentiomètre pour définir la tension de déblocage de la diode (origine du segment) un potentiomètre pour définir la pente du segment. Les premiers générateurs de fonction devaient être réglés manuellement, segment par segment. Puis vers 1970, sont apparus des dispositifs où chaque résistance variable était remplacée par un réseau de résistances commutées. Les commutateurs étaient actionnés à l'aide d'un lecteur de carte perforée statique, chaque trou potentiel dans la carte assurant ou non un contact. Les cartes, au format des cartes Hollerith, devaient être préparées sur calculateur numérique (tous munis à l'époque d'un perforateur de cartes). Un calculateur analogique « haut de gamme » ne comportait tout au plus qu'une demi douzaines de tels générateurs.

Les dispositifs de commande

Tout calculateur Analogique possède un système de boutons poussoirs permettant de définir ses différents états. Les trois principaux états sont :

« PS » (« Potentiometers Setting ») pour le réglage des potentiomètres représentant les coefficients constants des équations à résoudre aucune tension n'est appliquée aux opérateurs. Toutes les tensions sont figées à zéro.
« IC » (« Initial Conditions ») Les conditions initiales sont appliquées aux intégrateurs le temps est figé au temps $t=0$ . Un jeu de commutateurs convertit chaque intégrateur en un sommateur à une seule entrée, entrée spéciale pour la définition de la condition initiale (voir schéma), ce qui charge la capacité de l'intégrateur à la valeur voulue.
« C » (« Compute ») État calcul. Les commutateurs des intégrateurs basculent en position « intégrateur », les tensions évoluent avec le temps, de façon « analogue » au système physique dont on simule le comportement. On résout le système d'équations différentielles.

Il s'y ajoute souvent au moins deux états complémentaires

« H » (« Hold ») L'état mémoire permet au cours du calcul de figer le temps : le réseau d'entrée de chaque intégrateur est déconnecté, plus rien n'évolue. Permet de faire des mesures sur des points particuliers.
« SC » (« Static Check ») Souvent la valeur de condition initiale d'un intégrateur est nulle, ce qui ne permet pas de détecter facilement une erreur potentielle de câblage vers les autres opérateurs. L'état « Static Check » permet d'appliquer des conditions initiales factices qui ne servent qu'à des fins de vérification avant le lancement du calcul.

Le panneau d'interconnexion

Toutes les entrées et sorties des opérateurs sont regroupées sur un panneau de câblage amovible ce qui permet de passer rapidement d'un problème à un autre. Les interconnexions sont réalisées avec des câbles blindés pour minimiser les problèmes d'inductions et de parasites. Les fiches sont dorés afin d'assurer de bons contacts. Sur les « grands calculateurs » un panneau comporte plus de 4 000 trous.

Les équipements annexes

La tension de référence : Les conditions initiales sont définies à partir de la tension de référence dont la valeur est 1. Par définition. Toutes les mesures sont effectuées par rapport à cette tension de référence. Elle apparaît en de nombreux points sur le panneau de câblage, elle est fournie par une alimentation hautement stabilisée (sa valeur physique était couramment de 100 volts ou de 10 volts).
Voltmètre numérique : précision habituelle $10^{-4}$ . Il est associé à un sélecteur permettant à partir d'un clavier de mesurer toutes les sorties des opérateurs. Lors des conditions initiales et des tests statiques, il permet également de mesurer l'entrée des intégrateurs.
Enregistreurs et tables traçantes : Les résultats consistant en tensions électriques variables, ils peuvent être enregistrés sur des enregistreurs multivoie (souvent 8) mais le plus souvent , pour une meilleure précision de lecture sur des tables traçantes au format A3.
Calculateur numérique : À partir de 1970 il était possible d'associer au calculateur analogique un calculateur numérique, soit très puissant pour participer au calcul en temps réel (calculateur hybride), soit plus modestement pour automatiser la mise en œuvre du calculateur analogique : réglage des coefficients, vérification du bon fonctionnement des opérateurs et de la correction de leurs interconnexions, lancement des cycles de calcul et saisie des résultats en complément des traceurs.

Mise en œuvre

La forme générale d'un système d'équations différentielles soluble sur calculateur analogique est la suivante : $x'_{i}=\sum _{j}^{n}f_{i}(x_{j})$ , dans laquelle $f_{i}(x_{j})$ est une expression algébrique.

Il faut tout d'abord faire une correspondance entre grandeurs physiques et tensions électriques qui leur correspondent sur le calculateur analogiques. Sachant que les tensions électriques sorties des opérateurs analogiques doivent normalement évoluer entre + ou - la tension de référence qui vaut 1 par convention, on fait le plus souvent le changement de variable $X_{i}={\frac {x_{i}}{x_{imax}}}$ . Le plus souvent la variable indépendante (c.-à-d. celle par rapport à laquelle s'effectue la dérivation) est le temps $t$ , on lui fait correspondre le « temps machine » $T=at$ . On choisit $a=1$ pour une simulation en temps réel, $a<1$ pour une simulation ralentie, $a>1$ pour une simulation accélérée. Les changements de variables effectuées on obtient les équations « analogiques ».

Exemple d'un résonateur dont les équations analogiques sont $y''=-ay-by'$ avec les conditions initiales :

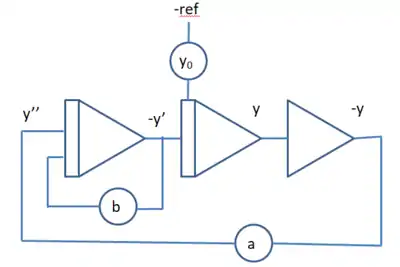
Schéma des connections entre les opérateurs d'un calculateur analogique représentant un résonateur.

Comparaison

Cette section ne cite pas suffisamment ses sources (février 2017).

Pour l'améliorer, ajoutez des références de qualité et vérifiables (comment faire ?) ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Le calculateur analogique présente les avantages suivants :

facilité de mise en œuvre pour la résolution des systèmes d'équations différentielles.
vitesse de calcul très élevée
hyper stable^[Quoi ?] puisque basé sur un phénomène physique^{[réf. nécessaire]}, à condition que la température des composants soit constante, ce qui implique salle climatisée et circuits toujours en opération. ;
fournit des résultats continus et continûment.
facilité de connexions avec des processus physiques externes

Le calculateur analogique présente les inconvénients suivants :

complexité des problèmes traitable absolument limitée par le nombre de ses opérateurs;
classe des problèmes traitable limité aux systèmes d'équations différentielles ordinaires
précision limitée par celle de ses composants : au mieux $10^{-4}$
manque de souplesse pour un calculateur universel (temps pour changer de problème)

Notes et références

Cet analyseur harmonique de Kelvin, ainsi que d'autres calculateurs mécaniques sont décrits dans Modern instruments and methods of calculation, éd. Bell & Sons, 1914, Édimbourg.
Cf. Laboratoire Derveaux, Le calculateur analogique Djinn type 20 AS, Boulogne-Billancourt, 1961, 47 p., 1 vol.; 27 cm
Cf. « PACE 231 R Analog Computer » [PDF], sur Computer history
Cf. « The EAI 8800 Scientific Computing System » [PDF], sur Computer history.
G. E. R. Cowan, R. C. Melville et Y. P. Tsividis, « A VLSI analog computer/digital computer accelerator », IEEE Journal of Solid-State Circuits, vol. 41, n^o 1,‎ janvier 2006, p. 42–53 (ISSN 0018-9200, DOI 10.1109/JSSC.2005.858618, lire en ligne, consulté le 7 juillet 2017)

Voir aussi

Bibliographie

Maurice Danloux-Dumesnils, Le Calcul analogique par courants continus, Paris : Dunod (impr. Jouve), 1963
Jean-Jacques Gleitz, Le calcul analogique, Paris : Presses universitaires de France, 1968
François Dattée, Calcul analogique, École supérieure d'électricité, 1969
Jean Helein, Calcul analogique et hybride, École supérieure d'électricité, 1969
J. Hugues et R.J. Pistenon, Calcul analogique, Paris : ENSTA, 1973
Annales de l'Association Internationale pour le Calcul Analogique (AICA), Collection 1958, vol. 1, 1975
Pierre Mounier-Kuhn, L'informatique en France, de la seconde guerre mondiale au Plan Calcul. L'émergence d'une science, Paris, PUPS, 2010. (ISBN 978-2-84050-654-6)
Cyrille Foasso, « Quand l'informatique était analogique », Pour la science, n^o 522,‎ avril 2021, p. 74-81

Articles connexes

Liens externes

Les calculateurs analogiques

Portail de l’informatique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Cet analyseur harmonique de Kelvin, ainsi que d'autres calculateurs mécaniques sont décrits dans Modern instruments and methods of calculation, éd. Bell & Sons, 1914, Édimbourg.

[DJINN-2] Cf. Laboratoire Derveaux, Le calculateur analogique Djinn type 20 AS, Boulogne-Billancourt, 1961, 47 p., 1 vol.; 27 cm

[231R-3] Cf. « PACE 231 R Analog Computer » [PDF], sur Computer history

[EAI.8800-4] Cf. « The EAI 8800 Scientific Computing System » [PDF], sur Computer history.

[5] G. E. R. Cowan, R. C. Melville et Y. P. Tsividis, « A VLSI analog computer/digital computer accelerator », IEEE Journal of Solid-State Circuits, vol. 41, n^o 1,‎ janvier 2006, p. 42–53 (ISSN 0018-9200, DOI 10.1109/JSSC.2005.858618, lire en ligne, consulté le 7 juillet 2017)