Oscillateur harmonique

Oscillation d'une masse suspendue à un ressort.

De nombreux systèmes physiques réels, pour lesquels on rend négligeable l'influence des frottements, se comportent comme des systèmes oscillants, qui peuvent être modélisés comme des oscillateurs harmoniques.

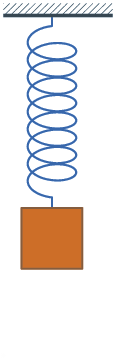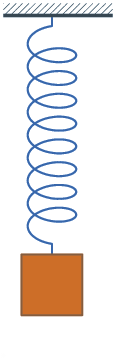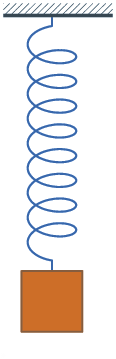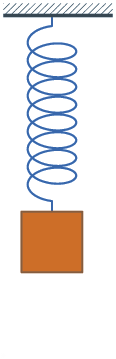
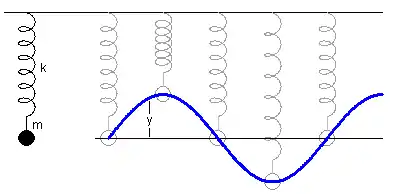
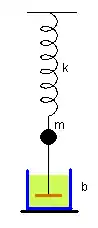
• Système masse-ressort: Il s'agit d'un système très simple à réaliser (cf. figure ci-contre). Si la masse est écartée légèrement de sa position d'équilibre et relâchée sans vitesse initiale, l'expérimentateur constate que celle-ci se met à osciller autour de cette position d'équilibre. La mesure, à l'aide d'un capteur adapté, de l'évolution au cours du temps de l'élongation x(t) du ressort (par rapport à la position où la masse est au repos) montre que les (petites) oscillations sont purement sinusoïdales, de pulsation ${\displaystyle \omega _{0}}$, du moins si l'influence des frottements est négligée[1]. La valeur de ${\displaystyle \omega _{0}}$ ne dépend pas de l'amplitude initiale de déplacement de la masse, mais uniquement de la valeur de la masse et des propriétés du ressort, plus précisément de sa raideur k.

Il est facile de montrer que l'équation du mouvement de la masse s'écrit ${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+\omega _{0}^{2}\,x(t)=0}$, avec ${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$.

Par suite l'équation horaire est donnée par ${\displaystyle x(t)=x_{m}\cos {(\omega _{0}t+\phi _{0})}}$, où ${\displaystyle x_{m}}$ est l'amplitude des oscillations et ${\displaystyle \phi _{0}}$ la phase à l'origine, qui dépendent des conditions initiales. Le mouvement est qualifiée d'harmonique, de pulsation propre ${\displaystyle \omega _{0}}$, la caractéristique du système.

Représentation schématique de l'évolution dans le temps de l'élongation de la masse m.

Les oscillations libres d'un circuit LC constituent un exemple d'oscillations harmoniques.

Courbe de la tension aux bornes du condensateur (en haut) et aux bornes de la bobine (en bas). Celles-ci sont en opposition de phase, montrant le transfert d'énergie entre le condensateur et la bobine.

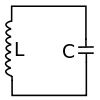
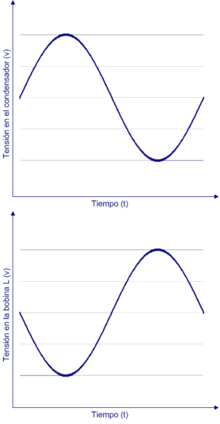
• Oscillations libres d'un Circuit LC: un condensateur de capacité électrique C, initialement chargé avec une charge ${\displaystyle q_{m}}$ commence à se décharger à un instant choisi comme origine dans une bobine d'inductance L, dont la résistance est considérée comme négligeable (cf. figure ci-contre). Il est facile de visualiser à l’oscilloscope l'évolution de la tension ${\displaystyle u_{C}(t)}$ aux bornes du condensateur, et donc celle de sa charge du fait de la relation ${\displaystyle u_{C}(t)={\frac {q(t)}{C}}}$[2]. Les résultats de mesures montrent que ${\displaystyle q(t)}$ a une évolution sinusoïdale pure au cours du temps, de fréquence ${\displaystyle \omega _{0}}$, dont la valeur ne dépend pas là encore de la charge initiale du condensateur, mais uniquement des valeurs de L et de C.

L'utilisation de la loi des mailles pour le circuit considéré permet de montrer que l'évolution de ${\displaystyle q(t)}$ obéit à l'équation différentielle ${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} t^{2}}}+\omega _{0}^{2}\,q(t)=0}$, avec ${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}$ pulsation propre des oscillations libres du circuit LC. Il vient l'expression ${\displaystyle q(t)=q_{m}\cos {(\omega _{0}t+\phi _{0})}}$ pour l'évolution de la charge du condensateur, les valeurs de l'amplitude ${\displaystyle q_{m}}$ et de la phase à l'origine ${\displaystyle \phi _{0}}$ dépendant des conditions initiales.

Les analogies entre l'oscillateur mécanique qu'est le système masse-ressort et l'oscillateur électrique qu'est le circuit LC permettent d'identifier entre elles certaines grandeurs mécanique et électrique (cf. plus bas: analogie électromécanique). Elles montrent aussi que les grandeurs permettant de caractériser l'état du système obéissent à une équation différentielle de même forme, dont les solutions sont harmoniques sinusoïdales. Il est ainsi possible de définir de façon générale un oscillateur harmonique comme un système dont l'évolution libre (non amortie du moins) est caractérisée par une équation de cette forme.

Illustration animée du mouvement harmonique unidimensionnel.

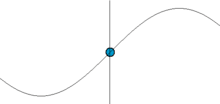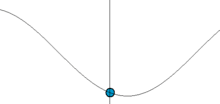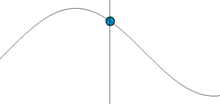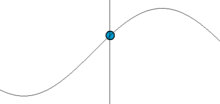
Les considérations expérimentales précédentes permettent de définir de façon générale un oscillateur harmonique, pour un système physique quelconque, "unidimensionnel" (ou à un degré de liberté), c'est-à-dire dont l'état peut être décrit à un instant t donné par une seule grandeur physique, notée s(t)[3]. La nature précise de cette grandeur physique dépend du système considéré (cf. exemples précédents).

Un tel système se comporte comme un oscillateur harmonique (idéal) si lorsque le système est "libre", c'est-à-dire pouvant être considéré comme isolé, la grandeur physique s(t) obéit à l'équation différentielle d'évolution suivante:

${\displaystyle {\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}+\omega _{0}^{2}\,s(t)=0}$, (1),

avec ${\displaystyle \omega _{0}}$ constante réelle positive, ayant les dimensions d'une fréquence, appelée pulsation propre[4] du système, qui ne dépend que des caractéristiques propres de celui-ci.

La solution générale de (1) ${\displaystyle s(t)=s_{m}\cos {(\omega _{0}t+\phi _{0})}}$, avec ${\displaystyle s_{m}=\mathrm {cte} }$ amplitude des oscillations et ${\displaystyle \phi _{0}=\mathrm {cte} }$ phase à l'origine, ces deux constantes étant déterminées par les conditions initiales sur s(t) et sa dérivée première.

Portrait de phase d'un pendule

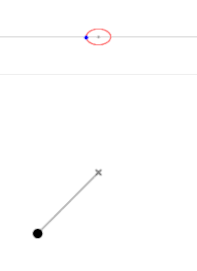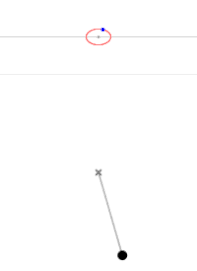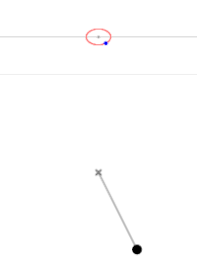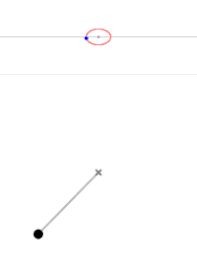
L'état de l'oscillateur à un instant donné est totalement déterminé par la connaissance de la position et de la vitesse. Puisque l'oscillateur n'a qu'un degré de liberté, un seul paramètre représente la position, et un seul la vitesse. Le portrait de phase d'un oscillateur harmonique est donc l'ensemble des trajectoires décrites par le système à partir de toutes les conditions initiales, représenté dans le plan ${\displaystyle \left(s,{\frac {\mathrm {d} s}{\mathrm {d} t}}\right)}$ .

Le portrait de phase d'un oscillateur harmonique libre est une ellipse.

Par définition un système idéal est un système dans lequel l'énergie totale est conservée, c'est-à-dire qu'elle demeure constante à travers le temps. Pour mettre l'aspect idéal de ce système en évidence et la signification physique de l'équation (1), il est très intéressant de multiplier celle-ci membre à membre par ${\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}$. Il vient alors :

${\displaystyle {\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}{\frac {\mathrm {d} s}{\mathrm {d} t}}+\omega _{0}^{2}\,{\frac {\mathrm {d} s}{\mathrm {d} t}}s(t)=0}$, soit encore ${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {1}{2}}\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}+{\frac {1}{2}}\,\omega _{0}^{2}\,s^{2}(t)\right]=0}$.

Par suite pour un oscillateur harmonique la quantité ${\displaystyle {\frac {1}{2}}\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}+{\frac {1}{2}}\,\omega _{0}^{2}\,s^{2}(t)=e}$ est conservée. Aux dimensions près, celle-ci correspond à l'énergie du système (de fait il sera toujours possible en pratique de multiplier e par des combinaisons de paramètres du système pour obtenir les "bonnes" dimensions).

Cette "énergie" est constituée de deux termes :

• un terme "d'énergie potentielle" en ${\displaystyle {\frac {1}{2}}\omega _{0}^{2}s^{2}(t)}$;
• un terme "d'énergie cinétique" en ${\displaystyle {\frac {1}{2}}\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}}$, (défini ici à une constante multiplicative près).

La forme quadratique de l'énergie "potentielle" est en fait caractéristique d'un oscillateur harmonique : en effet, ce n'est qu'avec cette forme que la prise en compte du caractère conservatif du système ${\displaystyle {\frac {\mathrm {d} e}{\mathrm {d} t}}=0}$ redonne l'équation d'évolution précédente.

Bien entendu, la nature exacte et les noms de ces termes dépendent du système étudié :

• pour le système masse-ressort, ${\displaystyle s(t)=x(t)}$, ${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=v(t)}$ est la vitesse instantanée de la masse à l'instant t, et ${\displaystyle \omega _{0}^{2}={\frac {k}{m}}}$. Par suite ${\displaystyle e={\frac {1}{2}}v^{2}(t)+{\frac {k}{2m}}x^{2}(t)}$ et il suffit de multiplier membre à membre par la masse m pour obtenir l'énergie mécanique du système ${\displaystyle E={\frac {1}{2}}mv^{2}(t)+{\frac {1}{2}}kx^{2}(t)}$: dans ce cas il s'agit bien de la somme de l'énergie cinétique et de l'énergie potentielle élastique de la masse m. Dans la limite où les frottements sont négligeables, cette énergie mécanique est conservée.
• pour le circuit LC, la grandeur s(t) est la charge q(t) de l'oscillateur à l'instant t, ${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}=i(t)}$ est l'intensité dans le circuit, et ${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}$. Par suite ${\displaystyle e={\frac {1}{2}}i^{2}(t)+{\frac {1}{2LC}}q^{2}(t)}$ et il suffit de multiplier membre à membre cette quantité par l'inductance L pour obtenir l'énergie du système ${\displaystyle E={\frac {1}{2}}Li^{2}(t)+{\frac {1}{2}}{\frac {q^{2}(t)}{C}}}$. Le terme en ${\displaystyle {\frac {1}{2}}Li^{2}(t)}$, qui correspond à l'énergie contenue dans la bobine, est l'analogue "électrique" de l'énergie cinétique du système masse-ressort, et celui en ${\displaystyle {\frac {1}{2}}{\frac {q^{2}(t)}{C}}}$, qui correspond à l'énergie stockée dans le condensateur, est l'analogue de l'énergie potentielle mécanique.

Comme ${\displaystyle s(t)=s_{m}\cos {(\omega _{0}t+\phi _{0})}}$, l'énergie du système peut alors s'écrire sous la forme ${\displaystyle e={\frac {1}{2}}\omega _{0}^{2}s_{m}^{2}}$ . L'énergie du système pour un oscillateur harmonique est donc proportionnelle au carré de l'amplitude des oscillations.

Le caractère conservatif de l'énergie d'un oscillateur harmonique idéal est bien sûr lié à l'absence de termes de dissipation. Il est en effet facile de voir que l'équation (1) est invariante par renversement du temps ${\displaystyle t\rightarrow -t}$ : une telle symétrie implique que l'énergie du système physique soit conservée (cf. théorème de Noether). Cette conservation de l'énergie totale du système implique qu'au cours de son évolution il y a transfert entre les formes "potentielle" et "cinétique" de l'énergie du système :

en fait, le caractère « oscillant » du système peut s'interpréter comme la conséquence du « va-et-vient » entre les deux formes d'énergie, dont la somme demeure (idéalement) constante au cours du temps.

Physiquement, un oscillateur harmonique présente la propriété fondamentale d'isochronisme des oscillations, c'est-à-dire que celles-ci possèdent une période donnée ${\textstyle T_{0}}$ (période propre), constante, au bout de laquelle elles se répètent à l'identique. Sur le plan fondamental, cette propriété résulte de l'invariance par translation dans le temps, qui elle-même implique le caractère conservatif de l'énergie du système[5]^,[6]. Sur le plan mathématique, l'invariance par translation dans le temps se traduit par l'absence de termes d'ordre impair en t, par exemple en ${\textstyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}$, dans l'équation différentielle d'évolution. En présence de frottements, la symétrie par translation dans le temps est brisée, et il n'y aura plus d'isochronisme des oscillations (cf. oscillateur harmonique amorti).

Bien qu'il s'agisse d'une idéalisation, le modèle de l'oscillateur harmonique est d'une importance fondamentale en Physique. En effet, tout système à un seul degré de liberté noté q(t), pour lequel il est possible de définir une énergie potentielle (notée ${\displaystyle V(q)}$ de façon générale) minimale en ${\displaystyle q=q_{m}}$, se comporte au voisinage de ce minimum comme un oscillateur harmonique.

En effet, au voisinage de ${\displaystyle q=q_{m}}$ l'énergie potentielle s'écrit ${\displaystyle V(q)=V(q_{m})+V'(q_{m})(q-q_{m})+{\frac {1}{2}}\left({\frac {\mathrm {d} ^{2}V}{\mathrm {d} q^{2}}}\right)_{q=q_{m}}\left(q-q_{m}\right)^{2}+O(q^{3})}$, avec ${\displaystyle V'(q_{m})=0}$ puisque ${\displaystyle V(q)}$ est minimale en ${\displaystyle q_{m}}$. De plus, ${\displaystyle k\equiv \left({\frac {\mathrm {d} ^{2}V}{\mathrm {d} q^{2}}}\right)_{q=q_{m}}>0}$ car l'équilibre doit être stable pour qu'il y ait des oscillations. En prenant l'origine de l'énergie potentielle en ${\displaystyle q=q_{m}}$, ${\displaystyle V(q_{m})=0}$, et en posant ${\displaystyle s(t)=q(t)-q_{m}}$, l'énergie potentielle se met au voisinage de tout minimum sous la forme de celle d'un oscillateur harmonique idéal :

${\displaystyle V(s)={\frac {1}{2}}\,k\,s^{2}(t)}$,

k étant une "constante de raideur" (par analogie avec le système masse-ressort) de l'oscillateur harmonique[7].

potentiel d'un pendule simple et son approximation parabolique

Exemple : pendule simple

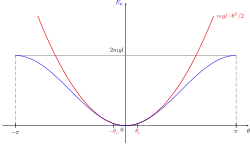
Dans le cas d'un pendule simple, le système est à un seul degré de liberté noté θ (angle entre la verticale et le fil), et l'énergie potentielle de la masse m (assimilée à un point matériel) est donnée par ${\displaystyle V(\theta )=mg\ell \left(1-\cos {\theta }\right)}$, g étant la pesanteur et ${\displaystyle \ell }$ la longueur du pendule. Cette énergie potentielle est clairement minimale en ${\displaystyle \theta _{m}=0}$ et au voisinage de cette position d'équilibre l'énergie potentielle du système s'écrit :

${\displaystyle V(\theta )\approx {\frac {1}{2}}\,m\,g\,\ell \,\theta ^{2}}$ puisque ${\displaystyle {\frac {\mathrm {d} ^{2}V}{\mathrm {d} \theta ^{2}}}=m\,g\,\ell \cos {\theta }}$, dans ce cas ${\displaystyle k=m\,g\,\ell }$. L'équation différentielle du mouvement est alors dans ce domaine celle d'un oscillateur harmonique : ${\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\,\theta =0}$, avec ${\displaystyle \omega _{0}={\sqrt {\frac {g}{\ell }}}}$ pulsation propre du pendule simple. Elle correspond à une linéarisation, dans la limite des petites oscillations, de l'équation "complète" ${\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\sin {\theta }=0}$ donnant l'évolution du pendule[8].

Dans le cas du pendule simple, l'approximation harmonique, dite aussi des petites oscillations, revient à remplacer le potentiel réel par le potentiel parabolique, caractéristique de l'oscillateur harmonique (cf. figure ci-contre).

Le modèle de l'oscillateur harmonique possède des limites de deux ordres.

En premier lieu, il correspond à la situation d'un système physique pris au voisinage d'un point d'équilibre stable comme indiqué précédemment. Si l'écart à l'équilibre est important, il apparaît en général des termes supplémentaires non quadratiques (dits anharmoniques) dans le développement de l'énergie potentielle.

Par ailleurs, il s'agit d'un modèle conservatif, qui néglige tous les termes de dissipation d'énergie, ou alors pour lequel ceux-ci sont exactement compensés par un apport extérieur d'énergie. Dans le premier cas, l'oscillateur harmonique est dit amorti, dans le second il est dit entretenu.

On peut dresser un parallèle entre l'oscillateur harmonique et la Corde de Melde. Cette dernière expérience permet de mettre en avant une infinité de pulsations possibles pour la corde tandis que le ressort lui ne peut osciller que selon une unique pulsation. Ceci est expliqué par l'inertie de la masse accrochée au ressort qui ne peut pas se subdiviser contrairement à la longueur de la corde à vide. Notons que le ressort seul, sans masse accrochée, pourrait à priori se comporter comme la Corde de Melde[9].

Pour tout système physique réel, le comportement n'est celui d'un oscillateur harmonique que dans un domaine restreint, même en négligeant tout terme de dissipation.

Par exemple, pour le système masse-ressort le système ne se comporte comme un oscillateur harmonique que dans la limite des petites oscillations, c'est-à-dire si l'on reste dans le domaine linéaire du ressort, où la force de rappel est proportionnelle à son élongation[10]. Pour des élongations plus élevées, il y a apparitions de termes non linéaires (dits anharmoniques) dans la relation force de rappel / élongation. Ceux-ci se caractérisent en pratique par l'apparition de termes en x^3 ou plus dans l'expression de l'énergie potentielle. Pour des élongations encore plus élevées, il y aura déformation permanente du ressort, qui quitte alors le domaine élastique pour entrer dans celui de la déformation plastique, voire se rompre. Dans ce cas-là la modélisation du système par une énergie potentielle ne sera pas possible.

Par ailleurs, il est fait l'hypothèse que le ressort revient toujours dans son état initial après déformation : en pratique, et même pour de petites élongations pour lesquelles le ressort reste dans le domaine élastique, ceci n'est pas strictement vérifié, du fait d'une certaine usure des matériaux du ressort. En fait, l'état réel du ressort dépend de son "histoire" (phénomène d'hystérésis) : cet effet est particulièrement visible sur un grand nombre d'oscillations et peut être modélisé par un terme d'amortissement dit structurel[11].

De façon générale, l'énergie d'un oscillateur harmonique sera donnée par une expression de la forme :

${\displaystyle E={\frac {1}{2}}\kappa \left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}+{\frac {1}{2}}\,\kappa \,\omega _{0}^{2}\,s^{2}(t)}$,

expression dans laquelle ${\displaystyle \kappa }$ représente un paramètre multiplicatif positif, dépendant du système considéré, et tel que E ait effectivement la dimension d'une énergie : ainsi pour un système masse-ressort ${\displaystyle \kappa =m}$, pour un circuit LC, ${\displaystyle \kappa =L}$, pour un pendule simple ${\displaystyle \kappa =m\,\ell ^{2}}$, etc.

Si la dissipation d'énergie est prise en compte, la relation ${\displaystyle {\frac {\mathrm {d} E}{\mathrm {d} t}}=0}$ traduisant le caractère conservatif du système n'est plus valide, et il faudra tenir compte de la puissance perdue par dissipation notée ${\displaystyle {\mathcal {P}}_{\rm {diss}}(t)}$, qui est toujours négative[12], et telle que :

${\displaystyle {\frac {\mathrm {d} E}{\mathrm {d} t}}={\mathcal {P}}_{\rm {diss}}(t)}$.

En règle générale, cette puissance des forces de dissipation n'a pas d'expression simple, et peut dépendre d'un très grand nombre de paramètres, parfois extérieurs au système considéré. Par exemple, pour un oscillateur mécanique, ce terme correspondra aussi bien à des forces dissipatives intérieures au système, traduisant les "frottements" entre ses différentes sous-parties, qu'à des forces extérieures, avec un transfert thermique entre le système et l'extérieur. En toute rigueur il faudrait alors utiliser une approche thermodynamique plutôt que purement mécanique[13].

Toutefois dans le cas où la dissipation est faible, et que les propriétés physiques du système sont considérées comme invariantes au cours du temps, il est possible de développer ${\displaystyle {\mathcal {P}}_{\rm {diss}}(t)}$ en puissance de ${\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}$.

A l'ordre le plus bas, l'expression de ${\displaystyle {\mathcal {P}}_{\rm {diss}}(t)}$ est alors de la forme[14] :

${\displaystyle {\mathcal {P}}_{\rm {diss}}=-\kappa \,\alpha \left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}}$,

${\displaystyle \alpha }$ étant un paramètre positif, supposé constant, ayant nécessairement les dimensions de l'inverse d'une durée[15] (cf. ci-après pour une discussion sur son interprétation physique).

Système masse-ressort amorti. La force d'amortissement visqueux est proportionnelle à la vitesse.

Sur le plan physique, une telle expression peut se justifier par le fait que l'introduction d'un terme de dissipation doit donner une équation différentielle qui ne soit plus invariante par renversement du temps, dont un terme en ${\textstyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}$ à l'ordre le plus bas, ce que seul peut réaliser un terme de dissipation dépendant de ${\textstyle \left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}}$ au moins.

• Dans le cas du système masse-ressort, cette expression correspond à celle de la puissance d'une force d'amortissement visqueux de la forme ${\displaystyle {\vec {f}}=-\lambda \,{\vec {v}}}$, avec ${\displaystyle \lambda >0}$.

Un montage expérimental permettant d'obtenir cette forme peut être celui de la figure ci-contre, où la masse est relié à un dispositif dissipateur plongeant dans un liquide, dont la viscosité peut être plus ou moins forte (cf. figure ci-contre à droite).

Circuit LC avec introduction d'une résistance R pour modéliser les pertes.

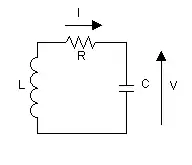
• Dans le cas du circuit LC, elle correspond à la prise en compte de la résistance R de la bobine et du reste du circuit pour modéliser les sources de pertes (cf. figure ci-contre à gauche).

La puissance dissipée par effet Joule dans celle-ci est donnée par ${\displaystyle P_{J}=R\,i^{2}(t)=r\left({\frac {\mathrm {d} q}{\mathrm {d} t}}\right)^{2}}$, ce qui correspond bien à l'expression proposée précédente.

Par suite, en tenant compte de cette expression approchée pour l'oscillateur faiblement amorti, il vient compte tenu de ${\displaystyle {\frac {\mathrm {d} E}{\mathrm {d} t}}={\mathcal {P}}_{\rm {diss}}(t)}$ l'équation différentielle donnant l'évolution de la grandeur s(t) :

${\displaystyle {\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}{\frac {\mathrm {d} s}{\mathrm {d} t}}+\omega _{0}^{2}\,{\frac {\mathrm {d} s}{\mathrm {d} t}}\,s(t)=-\alpha \left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}}$.

Contrairement au cas de l'oscillateur harmonique idéal, cette équation n'est pas symétrique par renversement du temps du fait du terme en ${\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}$, ce qui traduit sur le plan mathématique la non-conservation de l'énergie.

L'équation différentielle donnant l'évolution de l'oscillateur harmonique (faiblement) amorti peut être réécrite sous une forme plus physique en posant ${\displaystyle \alpha ={\frac {2}{\tau }}}$ ou ${\displaystyle \tau }$ est une durée caractéristique des processus de dissipation appelé temps de relaxation. Il vient alors :

${\displaystyle {\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}+{\frac {2}{\tau }}{\frac {\mathrm {d} s}{\mathrm {d} t}}+\omega _{0}^{2}\,s(t)=0}$.

La résolution mathématique de cette équation différentielle permet de distinguer trois régimes selon les valeurs relatives de ${\displaystyle \tau }$ et de la pulsation propre ${\displaystyle \omega _{0}}$ :

Allure de s(t) en régime sous-critique.

• régime dit pseudo-périodique : si ${\displaystyle \omega _{0}>{\frac {1}{\tau }}}$, il vient ${\displaystyle s(t)=Ae^{-{\frac {t}{\tau }}}\cos {(\omega t+\phi _{0})}}$, ce qui correspond à des oscillations sinusoïdales amorties de pseudo-fréquence[16] ${\displaystyle \omega =\omega _{0}{\sqrt {1-{\frac {1}{\tau ^{2}\omega _{0}^{2}}}}}<\omega _{0}}$, A et ${\displaystyle \phi _{0}}$ étant des constantes dépendant des conditions initiales. Il n'y a plus d'oscillations au sens strict mais s(t) prend la forme d'une sinusoïde dont l'enveloppe décroît exponentiellement au cours du temps (cf. figure ci-contre) : on parle alors d'oscillations libres amorties.

L'étude de la courbe représentative de ${\displaystyle s(t)}$ permet de déterminer la pseudo-période ${\displaystyle T={\frac {2\pi }{\omega }}}$ des oscillations, ainsi que le décrément logarithmique ${\displaystyle \delta \equiv \ln {\left({\frac {s(t)}{s(t+T)}}\right)}}$, qui est donné dans le cas du régime sous-critique par ${\displaystyle \delta ={\frac {T}{\tau }}}$. Ceci permet la mesure expérimentale du temps de relaxation ${\displaystyle \tau }$, caractéristique des phénomènes dissipatifs.

• régime critique : si ${\displaystyle \omega _{0}={\frac {1}{\tau }}}$, il vient ${\displaystyle s(t)=e^{-{\frac {t}{\tau }}}\left(At+B\right)}$, A et B étant deux constantes dépendant des conditions initiales. Il n'y a pas d'oscillations amorties, le système revient exponentiellement vers son état de repos. Il s'agit d'un cas limite.
• régime apériodique : si ${\displaystyle \omega _{0}<{\frac {1}{\tau }}}$, il vient ${\displaystyle s(t)=Ae^{-\beta _{+}{\frac {t}{\tau }}}+Be^{-\beta _{-}{\frac {t}{\tau }}}}$, avec ${\displaystyle \beta _{\pm }=1\pm {\sqrt {1-\omega _{0}^{2}\tau ^{2}}}\,>0}$, A et B étant deux constantes dépendant des conditions initiales. Il n'y a pas d'oscillations amorties, le système revient exponentiellement vers son état de repos.

On peut mettre en oscillation une masse soumise à l'action d'un ressort. On peut suivant les cas, réaliser des oscillations verticales ou des oscillations horizontales (en utilisant un dispositif permettant de minimiser les frottements sur le support).

Dans les deux cas, les oscillations sont harmoniques : la fonction du temps ${\displaystyle x(t)}$ de la position de la masse de part et d'autre de la position d'équilibre (statique) est une fonction sinus. La période est indépendante de l’amplitude (isochronisme des oscillations) : elle ne dépend que de l'inertie du système (masse m) et de la caractéristique de la force de rappel (constante de raideur k du ressort) : ${\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}.}$

La constante de raideur k est exprimée en N/m. Pour k = 1 N/m, il faudrait un Newton pour allonger le ressort d'un mètre. En réalité, la période dépend aussi de la masse du ressort, qui est négligée dans la formule ci-dessus. Voir l'article détaillé : système masse-ressort, pour une théorie plus complète.

Si les oscillations sont amorties par une force de frottement fluide (type visqueux à faible vitesse, force en ${\displaystyle -\alpha v}$), l'équation différentielle du mouvement peut s'écrire :

${\displaystyle m{\ddot {x}}+\alpha {\dot {x}}+kx=0.}$

Schéma d'un pendule de torsion

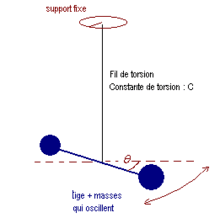
Le dispositif est constitué d'une barre fixée à un support par l'intermédiaire d'un fil de torsion : ce fil d'acier exerce un couple de rappel proportionnel à l'angle de torsion qu'on lui impose : ${\displaystyle -C\theta \,}$. Sur la barre on peut positionner deux masselottes de façon symétrique de façon à modifier le moment d'inertie.

La période est indépendante de l’amplitude (isochronisme des oscillations). Elle est donnée par la relation ci-dessous où J désigne le moment d'inertie de la barre munie des masselottes.

${\displaystyle T=2\pi {\sqrt {\frac {J}{C}}}.}$

Équation différentielle : ${\displaystyle J{\ddot {\theta }}+\alpha {\dot {\theta }}+C\theta =0.}$

Un circuit LC en électrocinétique est un circuit théorique comportant une bobine idéale : parfaitement inductive (inductance L et résistance nulle) et un condensateur (capacité C). Les deux dipôles sont en outre totalement linéaires, ce qui est le cas avec des bobines à noyau d'air mais qui ne l'est pas pour de bobines avec un noyau ferromagnétique.

Un tel circuit se comporte alors comme un oscillateur dont la période propre est : ${\displaystyle T_{0}=2\pi {\sqrt {LC}}.}$

De la loi des mailles : ${\displaystyle u_{L}+u_{C}=0\,}$, et des équations caractéristiques des deux dipôles : ${\displaystyle u_{L}=L\,{\frac {\mathrm {d} i}{\mathrm {d} t}}}$ et ${\displaystyle i=C\,{\frac {\mathrm {d} u_{C}}{\mathrm {d} t}}}$, on déduit :

${\displaystyle L\,C\,{\frac {\mathrm {d} ^{2}u_{C}}{\mathrm {d} t^{2}}}+u_{C}=0}$, avec ${\displaystyle u_{C}={\frac {q}{C}}\,.}$

L'équation différentielle peut donc s'écrire :

${\displaystyle L\,{\ddot {q}}+{\frac {q}{C}}=0.}$

Dans un circuit LC réel, on ne peut s'affranchir de la résistance. Celle-ci dissipe de l'énergie par effet joule. Dans ce cas, l'équation différentielle qui régit les oscillations (amorties) peut s'écrire : ${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=0.}$

Remarque : on peut entretenir les oscillations grâce à un montage dit à résistance négative.