Paquet d'onde gaussien

Dans le cadre de la mécanique quantique, on peut s'intéresser à la forme des solutions de l'équation de Schrödinger dans le cas d'une particule libre, c'est-à-dire telle que le potentiel auquel elle est soumise est nulle, ou ${\displaystyle V({\vec {r}},t)=0}$.

On peut alors montrer, en supposant une séparation des variables, que la solution la plus générale est une combinaison linéaire sur le paramètre continu k de la forme

Dans cette expression

• ${\displaystyle \omega (k)\ =\ {\frac {\hbar k^{2}}{2m}}}$
• ${\displaystyle {\vec {k}}}$ est un vecteur quelconque de ${\displaystyle \mathbb {R} ^{3}}$ tel que ${\displaystyle {\frac {\hbar ^{2}k^{2}}{2m}}=E}$
• ${\displaystyle E}$ est le paramètre de séparation des variables.
• Le facteur ${\displaystyle {\frac {1}{(2\pi )^{3/2}}}}$ est celui choisi pour symétriser la transformée de Fourier à trois dimensions.
• ${\displaystyle g({\vec {k}})}$ est le paquet d'ondes planes à trois dimensions.

Si l'on regarde la fonction d'onde en l'instant initial, donc en ${\displaystyle t=t_{0}}$, on s'aperçoit que ${\displaystyle \psi ({\vec {r}},t)}$ est la transformée de Fourier de ${\displaystyle g({\vec {k}})}$, et inversement. Ce résultat est tout à fait général et le fait que l'on puisse écrire ${\displaystyle \psi ({\vec {r}},t_{0})}$ sous forme d'une transformée de Fourier est également valable pour une particule non libre.

De plus, l'égalité de Parseval fournit

Ce qui assure que la fonction d'onde est normée si et seulement si ${\displaystyle g({\vec {k}})}$ l'est. Cette propriété est importante dans le sens où le carré de la norme de la fonction d'onde représente la probabilité de présence de la particule.

Paquet d'onde gaussien 1D, représenté dans le plan complexe, pour a=2 et k=4

Paquet d'onde gaussien 1D, représenté dans le plan complexe, pour a=1 et k=4

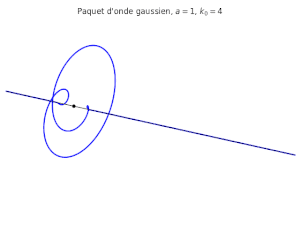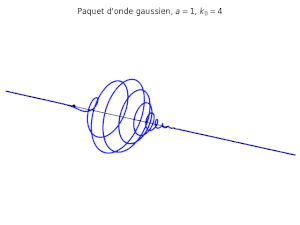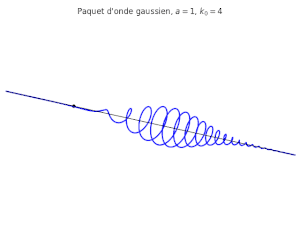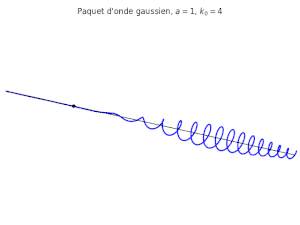
On peut considérer comme expression pour ${\displaystyle g({\vec {k}})}$ la fonction

${\displaystyle g({\vec {k}})={\frac {a^{3/2}}{(2\pi )^{3/4}}}e^{-{\frac {a^{2}}{4}}({\vec {k}}-{\vec {k_{0}}})^{2}}}$

qui constitue le paquet d'onde gaussien.

On peut alors démontrer les relations suivantes, à l'aide des formules de Poisson :

• ${\displaystyle \int |g({\vec {k}})|^{2}d^{3}k=1}$
• ${\displaystyle \psi ({\vec {r}},t_{0})=\left({\frac {2}{\pi a^{2}}}\right)^{3/4}e^{i{\vec {k_{0}}}.{\vec {r}}}e^{-r^{2}/a^{2}}}$

En repartant de l'expression générale de ${\displaystyle \psi ({\vec {r}},t)}$, on peut également démontrer que

${\displaystyle \psi ({\vec {r}},t)=\left({\frac {2a^{2}}{\pi }}\right)^{3/4}{\frac {1}{\left(a^{2}+{\frac {2i\hbar (t-t_{0})}{m}}\right)^{3/2}}}e^{i\phi (t)}e^{i{\vec {k_{0}}}.{\vec {r}}}e^{-{\frac {\left({\vec {r}}-{\frac {\hbar {\vec {k_{0}}}}{m}}(t-t_{0})\right)^{2}}{a^{2}+{\frac {2i\hbar (t-t_{0})}{m}}}}}}$

Où ${\displaystyle \phi (t)=-{\frac {\hbar k_{0}^{2}(t-t_{0})}{2m}}}$

En calculant le carré du module de cette fonction d'onde, on constate les éléments suivants:

• La densité de probabilité de présence de la particule est une gaussienne à trois dimensions.
• Dont l'amplitude décroît comme le temps.
• Dont le centre se déplace avec une vitesse ${\displaystyle {\vec {v_{0}}}={\frac {\hbar {\vec {k_{0}}}}{m}}}$.
• Dont la largeur augmente comme le temps.

Ces constatations font partie de l'indéterminisme quantique: la position d'une particule n'est plus décrite que par une probabilité de présence en tout temps t et tout lieu ${\displaystyle {\vec {r}}}$.

• C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique.

• Portail de la physique