Parapluie de Whitney
Le parapluie de Whitney est une surface présentant des auto-intersections dans l'espace ambiant de dimension 3. Elle doit son nom au mathématicien américain Hassler Whitney, qui a étudié cet objet au travers de ses travaux sur les singularités d'applications différentiables.
Pour les articles homonymes, voir Parapluie (homonymie).
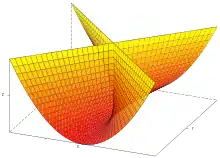
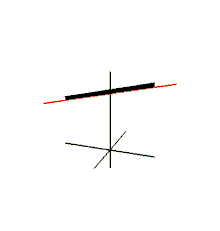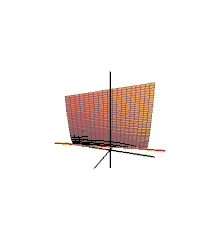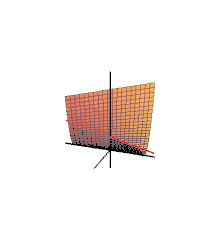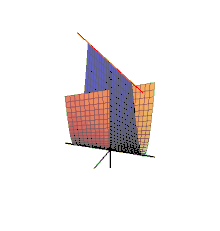
Formules
Les équations paramétriques de cette surface sont données en coordonnées cartésiennes par
où les paramètres u et v décrivent l'ensemble des réels. Cette surface est contenue dans celle donnée par l'équation implicite :
mais cette dernière inclut l'axe des z (aussi appelé poignée du parapluie), alors que la représentation paramétrique impose que z soit positif[1].
Propriétés
Il s'agit d'un objet d'étude important en théorie des singularités. Les applications génériques opérant sur des 2-variétés et à valeurs dans R3 ne présentent que deux types de singularités stables : les lignes où se recoupent la surface et le parapluie de Whitney (plus précisément le point inférieur). On doit à Whitney lui-même cette classification.
Le parapluie de Whitney est une surface réglée et même un conoïde droit, de directrice une parabole d'axe parallèle à son axe.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Whitney umbrella » (voir la liste des auteurs).
- Michel Coste, « Une sorcière, trois parapluies, un poisson », Images des mathématiques, (consulté le )
Bibliographie
- Vladimir Arnold, A. Varchenko et S. Goussein-Zadé, Singularités des applications différentiables, Moscou, Mir, 1984
- (en) « Whitney's Umbrella », The Topological Zoo, The Geometry Center (consulté le ) (Images and movies of the Whitney umbrella.)
- Portail de la géométrie