Pendule de Newton
Le pendule de Newton est un pendule se composant de cinq billes et permettant d'illustrer les théories de conservation de la quantité de mouvement et de l'énergie.

Description
Le pendule de Newton se compose de cinq billes métalliques de même masse suspendues par deux fils à deux barres rigides. Ces cinq billes se touchent au repos et sont situées dans le plan médian des deux barres. Son fonctionnement est fondé sur le principe des actions réciproques. La première loi de Newton stipule que le principe action-réaction est en vigueur.
Expériences
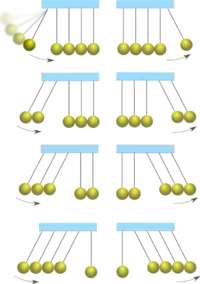
| Avant l'impact | Après l'impact |
|---|
Lorsqu'on lance deux billes, de l'autre côté deux billes se mettent en mouvement. Lorsqu'on lance trois billes, de l'autre côté les deux billes restantes se mettent en mouvement, accompagnées de la bille les ayant percutées. Il en est de même pour quatre billes.
Expériences plus méconnues : si l'on lance une bille de chaque côté en même temps, celles-ci rebondissent en même temps alors que les trois du milieu restent immobiles. De même, avec deux billes de chaque côté, la dernière bille est immobile. Si l'on lance trois billes d'un côté et deux de l'autre, elles se percutent et vont trois dans un sens, deux dans l'autre, alternativement.
Enlever une bille au repos alors qu'une autre effectue un mouvement de l'autre côté décale le mouvement d'une bille.
Il est possible de lancer plusieurs billes à des instants différents, afin d'augmenter le nombre de mouvements et de chocs, mais les résultats sont souvent faussés par les influences extérieures et par la non perfection du matériel.
Interprétation conservative
Le principe du pendule repose à la fois sur deux principes de conservation qui concernent respectivement l'énergie cinétique et la quantité de mouvement.
Cas où on lance une bille
L'interprétation est ici plus aisée en considérant un pendule avec uniquement deux billes. Dans cette analyse, les principes de conservation évoqués conduisent à un système de deux équations où les caractéristiques du pendule, avant et après la collision des billes, sont reliées. Avec les données de départ sur les billes que sont la vitesse initiale nulle de l'une d'entre elles et l'égalité de leur masse, la résolution du système permet de trouver la vitesse respective des deux billes après leur collision. On constate alors que l'effet du choc a simplement consisté en l'échange de la vitesse des deux billes.
Si on lance une bille d'un côté sur plusieurs autres immobiles, cette bille s'arrête après le choc tandis que celle située à l'autre extrémité se soulève en récupérant le mouvement de la bille initialement lancée.
Cas où on lance deux billes
Les deux billes de l'extrémité opposée se soulèvent car elles sont percutées par deux impacts éloignés temporairement de peu de temps[pas clair].
Cas où on lance trois billes ou plus
Pour le traitement mathématique de la collision d’une « chaîne » consistant en plus de 2 billes, les lois de conservation de la quantité de mouvement et de l’énergie cinétique ne sont plus suffisantes. Admettons qu’il y ait 5 billes ; les conditions initiales connues, on a besoin de 5 équations pour déterminer les 5 vitesses finales.
Effectivement, pour expliquer le comportement de la chaîne avec plus de 2 billes, il faut tenir compte d’une propriété particulière du dispositif : on considère la « chaîne » comme un système composé de masses et de ressorts (comme on le fait pour traiter les oscillations d’un réseau cristallin). Dans ce système se propage une onde. Ce n’est que si cette propagation se déroule sans dispersion, qu’il résulte le comportement observé avec les billes. Si les ressorts respectent la loi de Hooke, on a une forte dispersion, et l’expérience ne se déroule pas comme on l’observe avec les billes. Ceci se montre facilement sur un rail à coussin d’air. Un système de — par exemple — 5 chariots plus des ressorts comme butoirs ne se comporte pas comme les billes. Quand on lance deux chariots contre les trois autres qui se trouvent au repos, il résulte un mouvement assez chaotique. La non-dispersion de la chaîne de billes vient du fait que les ressorts équivalents qui correspondent à la pression d'une sphère sur une autre, n'est pas du tout du type loi de Hooke.
Histoire et éponymie
John Wallis, Christopher Wren et Christiaan Huygens présentèrent tous trois à la Royal Society en 1662 des mémoires décrivant les principes à l'œuvre dans ce pendule. Newton n'y a donc eu aucune part. René Descartes avait avant eux eu l'idée de la conservation du moment cinétique, mais sa solution du problème n'était pas complète.
Voir aussi
Article connexe
Liens externes
- Description des équations associées au pendule de Newton
- (en) Chris Schulz, « How Newton’s cradles work » — Texte d'introduction.
- Portail de la physique