Pendule inversé

La situation est exactement la même que celle décrite pour le pendule simple, en considérant une tige rigide mais de masse négligeable. On définit donc :

• θ l'angle formé entre la tige et la verticale ;
• m la masse du pendule ;
• l la longueur de la tige ;
• g l'accélération de la pesanteur ;

On note les dérivées temporelles par un point :

${\displaystyle {\dot {\theta }}={\frac {d\theta }{dt}}}$ et ${\displaystyle {\ddot {\theta }}={\frac {d{\dot {\theta }}}{dt}}}$.

On peut alors établir la période des oscillations :

${\displaystyle \omega _{0}^{2}={\frac {g}{l}}}$.

L'énergie cinétique est :

${\displaystyle E_{c}={\frac {ml^{2}{\dot {\theta }}^{2}}{2}}}$.

L'énergie potentielle de gravité :

${\displaystyle E_{p}=mgl(1+\cos \theta )}$.

Si le pendule est laissé libre, on peut écrire la conservation de l'énergie mécanique, ${\displaystyle E=E_{c}+E_{p}}$. Alors, on obtient :

${\displaystyle {\ddot {\theta }}-\omega _{0}^{2}\sin \theta =0}$.

La différence avec le pendule simple est que l'on s'intéresse à la situation θ ≈ π [2π] ; cela correspond à un maximum de l'énergie potentielle, c'est-à-dire à un équilibre instable.

Un pendule inversé sur un chariot

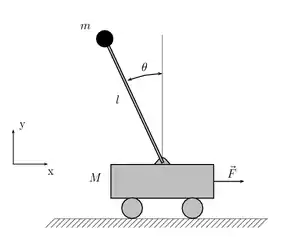
On peut établir les équations du mouvement à partir de la mécanique lagrangienne : en notant x(t) la position du chariot, ${\displaystyle \theta (t)}$ l'angle formé entre la tige et la verticale, le système étant soumis à la gravité et à une force F, extérieure et selon l'axe x, le lagrangien est :

${\displaystyle {\mathcal {L}}=T-V}$

avec T l'énergie cinétique et V l'énergie potentielle. On a ainsi :

${\displaystyle {\mathcal {L}}={\frac {1}{2}}Mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2}-mg\ell \cos \theta }$

avec ${\displaystyle v_{1}}$ la vitesse du chariot et ${\displaystyle v_{2}}$ celle de la masse ${\displaystyle m}$. On peut exprimer ${\displaystyle v_{1}}$ et ${\displaystyle v_{2}}$ à partir de x et ${\displaystyle \theta }$ :

${\displaystyle v_{1}^{2}={\dot {x}}^{2}}$

${\displaystyle v_{2}^{2}={\left({\dot {x}}-\ell {\dot {\theta }}\cos \theta \right)}^{2}+{\left(-\ell {\dot {\theta }}\sin \theta \right)}^{2}}$ ce qui s'écrit encore :

${\displaystyle v_{2}^{2}={\dot {x}}^{2}-2{\dot {x}}\ell {\dot {\theta }}\cos \theta +\ell ^{2}{\dot {\theta }}^{2}}$

Le lagrangien est donné par :

${\displaystyle {\mathcal {L}}={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}-m\ell {\dot {x}}{\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}-mg\ell \cos \theta }$

et les équations du mouvement sont donc :

${\displaystyle {\mathrm {d} \over \mathrm {d} t}{\partial {\mathcal {L}} \over \partial {\dot {x}}}-{\partial {\mathcal {L}} \over \partial x}=F}$

${\displaystyle {\mathrm {d} \over \mathrm {d} t}{\partial {\mathcal {L}} \over \partial {\dot {\theta }}}-{\partial {\mathcal {L}} \over \partial \theta }=0}$

En simplifiant ces équations, on obtient les équations, non linéaires, du mouvement du pendule :

${\displaystyle \left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F}$

${\displaystyle \ell {\ddot {\theta }}-{\ddot {x}}\cos \theta =g\sin \theta }$

• pendule ;
• Pendule paramétrique ;
• Pendule simple ;
• Théorème de Kapitza.

• Portail de la physique