Physique au-delà du modèle standard

La physique au-delà du modèle standard se rapporte aux développements théoriques de la physique des particules nécessaires pour expliquer les défaillances du modèle standard, telles que l'origine de la masse, le problème de la violation CP de l'interaction forte[1], les oscillations des neutrinos, l'asymétrie matière-antimatière, et la nature de la matière noire et de l'énergie noire. Un autre problème réside dans le cadre mathématique du modèle standard lui-même : son incompatibilité avec celui de la relativité générale, au point que l'une ou l'autre ou les deux théories deviennent inopérantes face à certaines conditions, par exemple les singularités gravitationnelles connues de l'espace-temps comme le Big Bang ou l'horizon des événements des trous noirs.

Les théories au-delà du modèle standard comprennent de nombreuses extensions du modèle standard jusqu'à la supersymétrie, telles que le modèle standard supersymétrique minimal[2] (en abrégé MSSM pour Minimal Supersymmetric Standard Model) et le Modèle standard supersymétrique quasi-minimal[3] (NMSSM pour Next to Minimal Supersymmetric Standard Model), ou des explications entièrement nouvelles telles que la théorie des cordes, la théorie M et les dimensions supplémentaires. Comme ces théories s'efforcent de reproduire l'intégralité de phénomènes ordinaires, l'identification de celle qui est correcte, ou au moins celle qui constitue la « meilleure avancée » vers la théorie du tout, peut seulement être réglée expérimentalement et constitue l'un des champs de recherche les plus actifs tant en physique théorique qu'en physique expérimentale.

Problèmes du modèle standard
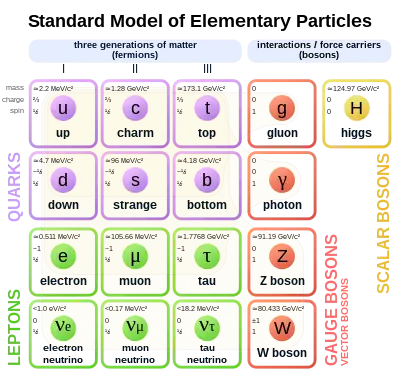
Le Modèle standard des particules élémentaires.

Bien qu'il constitue la théorie physique la plus réussie à ce jour, le modèle standard n'est pas parfait[4]. Une grande partie des résultats publiés par les physiciens théoriciens consiste à proposer différentes formes d'une nouvelle physique « au-delà du modèle standard », qui modifieraient le modèle standard de façon suffisamment subtile pour qu'il reste compatible avec les données existantes, tout en y apportant des rectifications suffisamment substantielles pour prédire les résultats selon le « modèle non standard » de nouvelles expériences qui seraient proposées.

Phénomènes non expliqués

De façon inhérente, le modèle standard est incomplet. Il existe dans la nature des phénomènes physiques qu'il ne peut expliquer convenablement.

  • la gravité : le modèle standard n'explique pas la gravité. L'approche naïve d'un simple ajout d'un « graviton[5] » au modèle standard ne récrée pas ce qui est observé expérimentalement sans nécessiter aussitôt d'autres modifications encore non découvertes au modèle standard. De plus, le modèle standard est largement considéré comme incompatible avec la théorie de la gravitation la plus précise à ce jour, la relativité générale[6].
  • La matière noire et l'énergie sombre[7] : les observations cosmologiques nous indiquent que le modèle standard n'explique qu'à peu près 4 % de l'énergie présente dans l'Univers. Des 96 % manquants, 27 % serait de la matière noire, qui se comporte exactement comme l'autre matière, mais n'interagit avec les champs du modèle standard qu'au moyen de l'interaction faible. Pourtant, le modèle standard ne présente aucune particule fondamentale comme bonne candidate pour la matière noire. Le reste des 96 % serait de l'énergie sombre, une densité d'énergie constante pour le vide. Les tentatives d'explication de l'énergie sombre en termes d'énergie du vide du modèle standard conduisent à une différence de 120 ordres de grandeurs[8].
  • La masse des neutrinos : selon le modèle standard, les neutrinos sont des particules sans masse. Cependant, des expériences sur l'oscillation des neutrinos ont montré qu'ils en ont effectivement une. La masse des neutrinos peut être rajoutée « à la main » au modèle standard, mais ceci conduit à de nouveaux problèmes théoriques. Par exemple, les termes de masse doivent nécessairement être extraordinairement petits, et la question n'a pas été clarifiée de savoir si la masse des neutrinos leur vient comme elle vient aux autres particules fondamentales du modèle standard.
  • L'asymétrie matière-antimatière : l'Univers est principalement constitué de matière. Cependant, le modèle standard prédit que la matière et l'antimatière ont dû être créées en quantités (presque) égales puisque les conditions initiales de l'Univers ne supposaient pas de disproportion entre l'une et l'autre. Pourtant aucun mécanisme n'apparaît suffisant dans le modèle standard pour expliquer cette asymétrie.

Résultats expérimentaux non expliqués

En physique des particules, c'est le niveau de 5 sigma (c'est-à-dire 5 déviations-standard) qui est le niveau largement admis pour qualifier le seuil d'une découverte scientifique. Or, de tous les résultats expérimentaux largement acceptés comme contradictoires au modèle standard, aucun n'est largement accepté comme le contredisant à ce niveau-là. Mais chaque expérience contient à quelques degrés des incertitudes statistiques ou systémiques. De plus, les prédictions théoriques ne sont pratiquement jamais calculées avec exactitude. Par surcroît, elles sont sujettes à des incertitudes dans la mesure des constantes fondamentales du modèle standard, certaines ténues, d'autres substantielles. On s'attend donc mathématiquement à ce que les résultats de quelques-unes des centaines d'expériences du modèle standard dérivent quelque peu de celui-ci, même sans découverte d'une « nouvelle physique ». À tout moment, il existe de nombreux résultats expérimentaux significativement différents des attentes du modèle standard, bien qu'on ait trouvé lors de la collecte de données supplémentaires que nombre d'entre eux étaient des hasards statistiques extraordinaires ou des erreurs expérimentales. D'un autre côté, toute physique « au-delà du modèle standard » devrait nécessairement se manifester expérimentalement en premier lieu par une différence statistique significative entre les résultats de l'expérience et ceux prédits théoriquement par le modèle standard.

Dans chaque cas, les physiciens cherchent à déterminer si un résultat constitue une simple coïncidence ou une erreur, d'un côté, ou bien, de l'autre, un signe d'une nouvelle physique. Des résultats statistiques supplémentaires concordants ne peuvent plus relever de la coïncidence, mais peuvent toujours résulter d'erreurs expérimentales ou d'une estimation imprécise de la précision expérimentale. Fréquemment, les expériences s'élaborent en vue d'une meilleure sensibilité aux résultats expérimentaux permettant de distinguer le modèle standard d'une alternative théorique.

Parmi les exemples les plus notoires se trouvent les suivants :

  • l'hydrogène muonique : le modèle standard présente des prédictions théoriques précises sur la taille du rayon atomique de l'hydrogène ordinaire, un système proton-électron et celui de l'hydrogène muonique, un système proton-muon, dans lequel le muon est un variant « lourd » de l'électron. Mais la mesure effective diffère sensiblement de la prédiction en utilisant les constantes physiques existantes, d'un ordre de 7 déviations-standard[9]. Des doutes sur la précision de l'estimation de l'erreur dans les expériences antérieures, toujours située dans les 4 % mutuels dans la mesure d'une distance très ténue, et l'absence d'une théorie bien motivée pouvant expliquer les divergences, ont rendu les physiciens hésitants quant à décrire ces résultats comme des contradictions au modèle standard, malgré l'apparence statistiquement significative du résultat et l'absence de toute possibilité clairement identifiée de source d'erreur expérimentale.
  • BaBar : des résultats d'une expérience BaBar pourraient suggérer par rapport aux prédictions du modèle standard un surplus d'un type de désintégrations de particules appelées . Dans celle-ci, un électron et un positron entrent en collision, il en résulte un méson B et un méson d'antimatière B-barre, qui se désintègrent ensuite en un méson D et un lepton tau ainsi qu'un neutrino plus léger. Alors que le niveau de certitude de l'excès (3,4 sigma) n'est pas suffisant pour prétendre à une percée au-delà du modèle standard, ces résultats signalent potentiellement une anomalie et sont susceptibles d'avoir des conséquences sur les théories existantes, y compris celles qui tentent de déduire les propriétés du boson de Higgs[10].

Prédictions théoriques non observées

Toutes les particules fondamentales prédites par le modèle standard ont été observées dans les accélérateurs de particules. Le boson de Higgs résulte du mécanisme de Higgs tel que l'explique le modèle standard, qui décrit comment est brisée la jauge de symétrie SU(2) et comment les particules fondamentales acquièrent de la masse. Il demeure (en date de 2014) la dernière particule prédite par le modèle standard à avoir été observée. Le , les scientifiques du CERN du grand collisionneur de hadrons (Large Hadron Collider, LHC) ont annoncé la découverte d'une particule compatible avec le boson de Higgs, de masse approximative 126 GeV/c2. L'existence d'un boson de Higgs a été confirmée le , alors même que l'on recherche encore la confirmation qu'il dispose de toutes les propriétés prévues par le modèle standard[11].

Certains hadrons, des particules composées de quarks, dont l'existence est prédite par le modèle standard, qui ne peuvent être produites qu'à de très hautes énergies, à très basses fréquences n'ont pas encore été définitivement observées, et les «boules de gluons »[12], des particules composées de gluons, n'ont pas encore été définitivement observées non plus. Certaines désintégrations de particules à basse fréquence prédites par le modèle standard n'ont pas encore été définitivement observées non plus, les données permettant d'effectuer une observation statistique significative n'étant pas disponibles.

Problèmes théoriques
Masse des particules fondamentales
  • supérieure à 80 GeV/c2
  • de 1 à 5 GeV/c2
  • de 90 à 110 MeV/c2
  • inférieure à 16 MeV/c2
  • sans masse

Certaines caractéristiques du modèle standard sont ajoutées de façon ad hoc. Elles ne constituent pas un problème en soi, c'est-à-dire que la théorie fonctionne convenablement avec ces caractéristiques ad hoc, mais elles suggèrent un défaut de compréhension. Ces caractéristiques ad hoc ont amené les théoriciens à explorer des voies nouvelles vers des théories plus fondamentales reposant sur un nombre inférieur de paramètres. Certaines des caractéristiques ad hoc sont :

  • Le problème de la hiérarchie. Le modèle standard introduit la masse des particules au travers d'un processus connu sous le nom de brisure spontanée de symétrie. Il résulte du champ de Higgs. À l'intérieur du modèle standard, la masse du Higgs admet certaines corrections quantiques très importantes du fait de la présence de particules virtuelles, principalement des quarks top virtuels. Ces corrections sont beaucoup plus grandes que la masse réelle du Higgs. Ceci signifie que le paramètre de masse nue (en) du Higgs dans le Modèle standard doit être finement ajusté de façon à annuler presque complètement les corrections quantiques. Ce niveau d'ajustement est estimé par de nombreux théoriciens comme non naturel.
  • Le problème de la violation CP de l'interaction forte. On peut théoriquement soutenir que le modèle standard devrait contenir un terme qui brise la symétrie CP, celle qui relie la matière à l'antimatière dans le secteur de l'interaction faible. Cependant, aucune observation de ce genre de violation n'a eu lieu lors d'une expérience, ce qui suggère que le coefficient de ce terme est extrêmement proche de zéro. Cet ajustement fin est également considéré comme non naturel.
  • Le nombre de paramètres. Le modèle standard dépend de 19 paramètres numériques. Leur valeur est connue expérimentalement, mais l'origine de ces valeurs est inconnue. Certains théoriciens ont essayé d'établir des relations entre différents paramètres, par exemple entre les masses des particules de différentes générations.

Théories de la grande unification

Le modèle standard a trois jauges de symétries : la symétrie de couleur SU(3), d'isospin faible SU(2), et d'hypercharge U(1), correspondant aux trois forces fondamentales. Du fait de la renormalisation, les constantes de couplage de chacune de ces symétries varient avec l'énergie auxquelles elles sont mesurées. Aux alentours de 16 GeV, ces couplages s'égalisent approximativement. Ce qui a conduit à spéculer sur le fait qu'au-dessus de ces énergies, les trois jauges de symétrie du modèle standard sont unifiées en une seule jauge de symétrie avec un groupe de jauge simple et une seule constante de couplage. En dessous de ces énergies, la symétrie, est spontanément brisée par rapport à celles du modèle standard[13]. C'est le groupe unitaire spécial à cinq dimensions SU(5) et le groupe spécial orthogonal à dix dimensions SO(10) qui sont les plus populaires pour les choix de ces groupes d'unification[14].

Les théories qui unifient les symétries du modèle standard de cette façon s'appellent les théories de la grande unification (ou GUT pour Grand Unified Theories, en anglais), et l'échelle d'énergie auxquelles la symétrie unifiée est brisée est appelée l'échelle GUT. Génériquement, les théories de la Grande unification prévoient la création de monopôles magnétiques lors de l'Univers primorial[15] et l'instabilité du proton[16]. Aucune des deux n'a été observée à ce jour, et cette absence introduit des limites aux GUT possibles.

Supersymétrie

La supersymétrie élargit le modèle standard en ajoutant des classes de symétries supplémentaires au lagrangien. Ces symétries échangent des particules fermioniques et bosoniques. Ce genre de symétrie prédit l'existence de particules supersymétriques, les sparticules, comprenant les sleptons, les squarks, les neutralinos et les charginos. Chaque particule du Modèle standard est supposée avoir un superpartenaire dont le spin diffère d'1/2 de celui de la particule ordinaire. Du fait de la brisure de supersymétrie, les sparticules sont beaucoup plus lourdes que leurs contreparties ordinaires. Elles sont si lourdes que les accélérateurs de particules existants ne disposent pas d'une puissance suffisante pour les produire.

Neutrinos

Dans le modèle standard, les neutrinos ont une masse exactement nulle. Ceci résulte du modèle standard ne contenant que des neutrinos d'hélicité gauche. Sans partenaire convenable avec une hélicité droite, il est impossible d'ajouter un terme de masse renormalisable au modèle standard[17]. Les mesures ont cependant indiqué des changements de saveurs des neutrinos, ce qui implique qu'ils ont une masse. Ces mesures ne donnent que la masse relative des différentes saveurs. La meilleure contrainte sur la masse absolue des neutrinos provient de mesures de précision de la désintégration du tritium, qui fixe une limite supérieure à 2 eV, soit plus légers d'au moins cinq ordres de magnitudes que les autres particules du modèle standard[18]. Ceci rend nécessaire une extension du modèle standard, qui non seulement souffre d'une absence d'explication de la façon dont les neutrinos acquièrent une masse, mais également pourquoi celle-ci est si faible[19].

Une façon d'ajouter de la masse aux neutrinos, appelée Mécanisme de see-saw, consiste à ajouter des neutrinos dextrogyres, et les coupler avec des neutrinos lévogyres[20] à l'aide d'un terme de masse de Dirac. Les neutrinos dextrogyres doivent être stériles, ce qui signifie qu'ils ne participent à aucune des interactions du Modèle standard. N'ayant aucune charge, les neutrinos dextrogyres peuvent constituer leur propre anti-particules, et avoir un terme de masse de Majorana. Comme les autres masses de Dirac dans le modèle standard, on s'attend à ce que la masse de Dirac du neutrino soit générée au moyen du mécanisme de Higgs, et ne peut de ce fait pas être prédite. Les masses de fermions du Modèle standard diffèrent de plusieurs ordres de magnitude ; la masse de Dirac du neutrino présente au minimum la même incertitude. La masse de Majorana pour les neutrinos dextrogyres doit survenir au moyen du modèle standard de Higgs et l'on s'attend de ce fait à ce qu'il soit lié à quelque échelle d'énergie de la nouvelle physique au-delà du modèle standard[21]. Ainsi, tout processus impliquant des neutrinos dextrogyres sera supprimé aux basses énergies. La correction due à ces processus supprimés donne effectivement aux neutrinos lévogyres une masse inversement proportionnelle à la masse de Majorana dextrogyre, mécanisme connu sous le nom de see-saw (balancier)[22]. Ainsi, la présence de neutrinos dextrogyres lourds explique aussi bien la faible masse des neutrinos lévogyres que leur propre absence dans les observations. Cependant, du fait de l'incertitude des masses du neutrino de Dirac, les masses du neutrino dextrogyre peuvent se situer n'importe où. Par exemple, ils peuvent être aussi légers que quelques keV et constituer la matière noire[23], ils peuvent avoir une masse compatible avec le domaine d'énergie du LHC[24],[25] et mener à des violations observables des nombres leptoniques[26], ou encore se trouver à proximité de l'échelle de la théorie de la grande unification, reliant ainsi le neutrino dextrogyre à la possibilité d'une telle théorie[27],[28].

Les termes de masse mélangent différentes générations de neutrinos, selon un paramétrage par la matrice PMNS, qui est l'analogue pour le neutrino de la matrice CKM de mélange des quarks. Au contraire du mélange des quarks, presque minimal, le mélange des neutrinos paraît presque maximal. Ceci conduit à de nombreuses spéculations sur les symétries entre les différentes générations qui expliqueraient le mode de mélange[29]. La matrice de mélange peut aussi contenir plusieurs phases complexes qui brisent l'invariance CP, bien qu'il n'en existe aucune preuve expérimentale. Ces phases pourraient potentiellement avoir créé un surplus de leptons par rapport aux anti-leptons dans l'Univers primordial, processus connu sous le nom de leptogénèse. Cette asymétrie peut s'être ultérieurement convertie en un excès des baryons par rapport aux anti-baryons, et expliquer l'asymétrie matière-antimatière observée dans l'Univers[14].

Les neutrinos légers ne peuvent pas expliquer la matière noire, faute d'une masse suffisante. De plus, les simulations de formations des structures montrent qu'ils sont trop chauds, c'est-à-dire que leur énergie cinétique est grande en comparaison de leur masse, alors que la formation de structures similaires aux galaxies de notre univers requiert de la matière noire froide. Les simulations montrent que les neutrinos peuvent au mieux expliquer un faible pourcentage de la matière noire. Toutefois, les neutrinos stériles dextrogyres sont des candidats possibles pour des WIMPs de matière noire[30].

Les modèles de préon

Plusieurs modèles de préon ont été proposés pour résoudre le problème persistant des trois générations de quarks et de leptons. Les modèles de préons postulent généralement de nouvelles particules, présentées ensuite comme étant capables de se combiner pour former les quarks et les leptons du modèle standard. Un des premiers modèles de préon fut le modèle de Rishon[31],[32],[33].

À ce jour, aucun modèle de préon n'a été vérifié et, conséquemment, largement accepté.

Les théories du tout

La théorie du tout

La physique théorique continue ses efforts vers une théorie du tout, qui expliquerait entièrement et lierait ensemble tous les phénomènes physiques connus, et prédirait les résultats de n'importe quelle expérience conduite selon ses principes. En pratique, l'objectif immédiat dans cette perspective vise au développement d'une théorie unissant le modèle standard et la relativité générale en une théorie de la gravité quantique. Des améliorations supplémentaires sont attendues, telles que la résolution de défauts conceptuels de l'une ou l'autre de ces théories préexistantes, ou bien une prédiction précise de la masse des particules. Les défis dans la construction d'une telle théorie ne sont pas que conceptuels, ils comprennent les aspects expérimentaux des très hautes énergies, nécessaires pour explorer ces domaines exotiques. La supersymétrie, la théorie des cordes et la gravitation quantique à boucles comptent parmi les nombreuses tentatives notoires dans cette direction.

La théorie des cordes

Il existe des extensions, révisions, remplacements et réorganisations du modèle standard, comme des essais de corriger ces problèmes et d'autres. La théorie des cordes compte parmi ces réinventions, et de nombreux physiciens théoriciens pensent ces théories comme la prochaine étape vers la théorie du tout. Des théories de gravité quantique comme la gravitation quantique à boucles ou d'autres sont considérées par certains d'entre eux comme des candidats prometteurs à l'unification mathématique de la théorie des champs quantiques et de la relativité générale, exigeant moins de changements drastiques aux théories existantes[34]. Cependant, des travaux récents fixent des limites impérieuses aux effets putatifs de la gravité quantique sur la vitesse de la lumière, et compromettent certains des modèles de gravité quantique[35].

Parmi les nombreuses variantes de la théorie des cordes, la théorie M, dont l'existence mathématique a été pour la première fois proposée à la Conférence sur les cordes en 1995, est considérée comme une candidate convenable pour la théorie du Tout, notamment par les physiciens Brian Greene et Stephen Hawking. Bien qu'il n'en existe pas encore de description mathématique complète, des solutions à cette théorie existent pour certains cas spécifiques[36]. Des travaux récents ont également proposé des modèles de cordes alternatifs, dont certains ne présentent pas les nombreuses caractéristiques difficiles à expérimenter de la théorie M (par exemple l'existence de variétés de Calabi–Yau, de nombreuses dimensions supplémentaires, etc.), comprenant des travaux par des physiciens aux publications appréciées, telles que Lisa Randall[37],[38].

Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « New physics » (voir la liste des auteurs).
  1. Voir l'article en:Strong_CP_problem sur la version anglaise de Wikipédia.
  2. Voir l'article en:Minimal Supersymmetric Standard Model sur la version anglaise de Wikipédia.
  3. Voir l'article en:Next-to-Minimal Supersymmetric Standard Model sur la version anglaise de Wikipédia.
  4. J. D. Lykken, CERN Yellow Report (Rapport jaune du CERN), CERN, , 101–109 p. (arXiv 1005.1676), « Beyond the Standard Model (Au-delà du Modèle standard) ».
  5. dont, s'il existe, les propriétés reçoivent un consensus considérable parmi les physiciens.
  6. A. O. Sushkov, W. J. Kim, D. A. R. Dalvit et S. K. Lamoreaux, « New Experimental Limits on Non-Newtonian Forces in the Micrometer Range (Nouvelles limites expérimentales des forces non newtoniennes dans le domaine micrométrique) », Physical Review Letters, vol. 107, no 17,‎ , p. 171101 (DOI 10.1103/PhysRevLett.107.171101, Bibcode 2011PhRvL.107q1101S, arXiv 1108.2547) :
    « il est remarquable que deux des succès les plus brillants de la physique du XXe siècle, la Relativité générale et le Modèle standard, apparaissent comme fondamentalement incompatibles »
    mais voir également John F. Donoghue, « The effective field theory treatment of quantum gravity (Le traitement efficace de la théorie des champs de la gravité quantique) », AIP Conference Proceedings (Compte-rendu de conférences de l'Institut de Physique Américain)., vol. 1473,‎ , p. 73 (DOI 10.1063/1.4756964, arXiv 1209.3511) :
    « On trouve dans la littérature des centaines d'affirmations selon lesquelles « la relativité générale et la mécanique quantique sont incompatibles ». Elles sont complètement dépassées et plus guère adaptées. La théorie des champs en vigueur montre que la relativité générale et la mécanique quantique œuvrent ensemble parfaitement normalement sur un large éventail d'échelles et de courbures, y compris celles concernant le monde que nous voyons autour de nous. Cependant les théories des champs en vigueur ne sont valables que pour certains domaines d'échelles. La relativité générale présente assurément des problèmes aux échelles extrêmes. Il existe des problèmes importants que la théorie des champs en vigueur ne résout pas parce qu'ils se trouvent au-delà de son domaine de validité. Cependant, ceci signifie que la question avec la gravité quantique n'est pas celle que nous supposions. Plutôt qu'un incompatibilité fondamentale entre la mécanique quantique et la gravité, nous sommes dans la situation plus familière où nous avons besoin d'une théorie plus complète au-delà du domaine de leur incompatibilité combinée. Le mariage habituel de la relativité générale et de la mécanique quantique fonctionne correctement aux énergies ordinaires, mais nous cherchons maintenant à découvrir les modifications qui doivent être présentes dans des conditions plus extrêmes. Ceci constitue la vision moderne du problème de la gravité quantique, et elle représente un progrès sur la vision désuète du passé." »
  7. J. Womersley, « Beyond the Standard Model (Au-delà du modèle standard) », sur Symmetry Magazine, (consulté le ).
  8. Krauss, L. (2009). = 7ImvlS8PLIo A Universe from Nothing. AAI Conference.
  9. Randolf Pohl, Ronald Gilman, Gerald A. Miller, Krzysztof Pachucki, "Muonic hydrogen and the proton radius puzzle" (May 30, 2013) https://arxiv.org/abs/1301.0905 in print Annu. Rev. Nucl. Part. Sci. Vol 63 (2013) 10.1146/annurev-nucl-102212-170627 ("La détermination récente du rayon du proton en utilisant la mesure du décalage de Lamb dans l'hydrogène muonique a fait sursauter le monde de la physique. Les valeurs obtenues de 0.84087(39) fm diffèrent de l'ordre de 4%% ou 7 déviations-standard de la valeur du CODATAde 0.8775(51) fm. Cette dernière se compose à partir de la valeur de l'atome de l'hydrogénat muonique de 0.8758(77) fm et d'une valeur similaire avec de plus grandes incertitudes déterminées par la dispersion de l'électron.")
  10. J. P. Lees, « Evidence for an excess of B → D(*)τ−τν decays », Physical Review Letters, vol. 109, no 10,‎ (DOI 10.1103/PhysRevLett.109.101802, Bibcode 2012PhRvL.109j1802L, arXiv 1205.5442).
  11. C. O'Luanaigh, « New results indicate that new particle is a Higgs boson », CERN, .
  12. (en) Marco Frasca, « What is a Glueball? », (consulté le ).
  13. M. E. Peskin et D. V. Schroeder, An introduction to quantum field theory, Addison-Wesley, , 786–791 p. (ISBN 978-0-201-50397-5).
  14. (en) W. Buchmüller « Neutrinos, Grand Unification and Leptogenesis », .
  15. D. Milstead et E.J. Weinberg, « Magnetic Monopoles », Particle Data Group, (consulté le ).
  16. P. Nath et P. F. Perez, « Proton stability in grand unified theories, in strings, and in branes », Physics Reports, vol. 441, nos 5–6,‎ , p. 191–317 (DOI 10.1016/j.physrep.2007.02.010, Bibcode 2007PhR...441..191N, arXiv hep-ph/0601023).
  17. M. E. Peskin et D. V. Schroeder, An introduction to quantum field theory (Introduction à la théorie des champs quantiques), Addison-Wesley, , 713–715 p. (ISBN 978-0-201-50397-5).
  18. Nakamura, K.; et al. (Particle Data Group), « Neutrino Properties (Propriétés des neutrinos) », Particle Data Group, (consulté le ).
  19. R. N. Mohapatra et P. B. Pal, Massive neutrinos in physics and astrophysics (Neutrinos massifs en physique et en astrophysique), vol. 72, World Scientific, , 3e éd., 451 p. (ISBN 978-981-238-071-5, lire en ligne).
  20. autrement dit, respectivement, de chiralité droite et gauche
  21. (en) G. Senjanovic « Probing the Origin of Neutrino Mass: from GUT to LHC (A la recherche de l'origine de la masse des neutrinos : de la GUT au LHC) », .
  22. (en) Y. Grossman « TASI 2002 lectures on neutrinos Conférence TASI sur les neutrinos 2002) », .
  23. S. Dodelson et L. M. Widrow, « Sterile neutrinos as dark matter (Les neutrinos stériles comme matière noire) », Physical Review Letters, vol. 72,‎ , p. 17 (DOI 10.1103/PhysRevLett.72.17, Bibcode 1994PhRvL..72...17D, arXiv hep-ph/9303287).
  24. P. Minkowski, « μ → e γ at a Rate of One Out of 109 Muon Decays? », Physics Letters B, vol. 67, no 4,‎ , p. 421 (DOI 10.1016/0370-2693(77)90435-X, Bibcode 1977PhLB...67..421M).
  25. R. N. Mohapatra et G. Senjanovic, « Neutrino mass and spontaneous parity nonconservation (La masse du neutrino et la nonconservation spontanée de la parité) », Physical Review Letters, vol. 44, no 14,‎ , p. 912 (DOI 10.1103/PhysRevLett.44.912, Bibcode 1980PhRvL..44..912M).
  26. W.-Y. Keung et G. Senjanovic, « Majorana Neutrinos And The Production Of The Right-handed Charged Gauge Boson (Les neutrinos de Majorana et la production de bosons de jauge chargés dextrogyre) », Physical Review Letters, vol. 50, no 19,‎ , p. 1427 (DOI 10.1103/PhysRevLett.50.1427, Bibcode 1983PhRvL..50.1427K).
  27. M. Gell-Mann, P. Ramond et R. Slansky, Supergravity, North Holland (P. van Nieuwenhuizen et D. Freedman), .
  28. S. L. Glashow, Proceedings of the 1979 Cargèse Summer Institute on Quarks and Leptons (Compte-rendu de l'Institut d'été sur les quarks et les leptons de Cargèse, 1979), M. Levy Plenum Press, .
  29. (en) Altarelli « Lectures on Models of Neutrino Masses and Mixings (Conférence sur les modèles de masse et de mélange des neutrinos) », .
  30. (en) H. Murayama « Physics Beyond the Standard Model and Dark Matter (La physique au-delà du Modèle standard et la matière noire) », .
  31. (en) H. Harari, « A Schematic Model of Quarks and Leptons », Physics Letters B, vol. 86, no 1,‎ , p. 83-86.
  32. (en) M. A. Shupe, « A Composite Model of Leptons and Quarks », Physics Letters B, vol. 86, no 1,‎ , p. 87-92.
  33. (en) P. Zenczykowski, « The Harari-Shupe preon model and nonrelativistic quantum phase space », Physics Letters B, vol. 660, no 5,‎ , p. 567-572.
  34. Lee Smolin, Three Roads to Quantum Gravity (Trois voies vers la gravité quantique), Basic Books, (ISBN 0-465-07835-4).
  35. A. A. Abdo, « A limit on the variation of the speed of light arising from quantum gravity effects (Limite à la variation de la vitesse de la lumière survenant des effets de la gravité quantique) », Nature, vol. 462, no 7271,‎ , p. 331 (PMID 19865083, DOI 10.1038/nature08574, Bibcode 2009Natur.462..331A, arXiv 0908.1832, lire en ligne).
  36. Juan Maldacena, A. Strominger et Edward Witten, « Black hole entropy in M-Theory (Entropie des trous noirs dans la théorie M) », Journal of High Energy Physics, vol. 1997, no 12,‎ , p. 2 (DOI 10.1088/1126-6708/1997/12/002, Bibcode 1997JHEP...12..002M, arXiv hep-th/9711053).
  37. Lisa Randall et R. Sundrum, « Large Mass Hierarchy from a Small Extra Dimension (Grande hiérarchie des masses à partir d'une petite dimension supplémentaire) », Physical Review Letters, vol. 83, no 17,‎ , p. 3370 (DOI 10.1103/PhysRevLett.83.3370, Bibcode 1999PhRvL..83.3370R, arXiv hep-ph/9905221).
  38. Lisa Randall et R. Sundrum, « An Alternative to Compactification (Une alternative à la compacification) », Physical Review Letters, vol. 83, no 23,‎ , p. 4690 (DOI 10.1103/PhysRevLett.83.4690, Bibcode 1999PhRvL..83.4690R, arXiv hep-th/9906064).

Voir aussi

Bibliographie
  • (en) Lisa Randall, Warped Passages : Unraveling the Mysteries of the Universe's Hidden Dimensions [« Passages entortillés : démêler les mystères des dimensions cachées de l'Univers »], New York, HarperCollins, , 499 p. (ISBN 0-06-053108-8)
  • « Physique des particules : Dépasser le modèle standard ? », Pour la science, hors série no 114,‎ , p. 1-119

Articles connexes

Liens externes
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.