Polyèdre de Szilassi
Le polyèdre de Szilassi, créé en 1977 par le mathématicien hongrois Lajos Szilassi (hu) (né en 1942 [1]), est un polyèdre comportant un trou, 7 faces de six côtés chacune ayant une arête commune avec les six autres, 14 sommets et 21 arêtes.
| Polyèdre de Szilassi | |
|---|---|
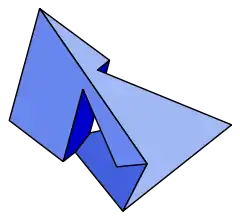 | |
| Type | Polyèdre homéomorphe au tore |
| Faces | 7 faces hexagonales |
| Arêtes | 21 |
| Sommets | 14 |
| Caractéristique d'Euler | 0 |
| Genre | 1 |
| Vertex configuration | 6.6.6 |
| Symmetry group | ? |
| Dual | Polyèdre de Császár |
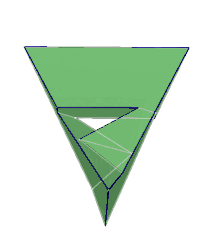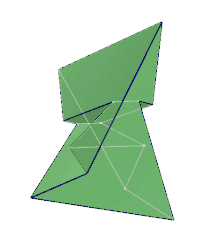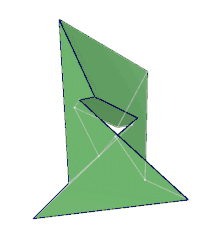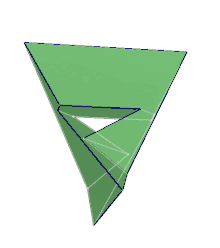
Un tel objet était considéré comme inconcevable avant lui [2], quoiqu'il s'agisse du dual du polyèdre de Császár, décrit en 1949 par Ákos Császár.
Sept couleurs sont nécessaires pour colorier les faces de ce polyèdre de telle sorte que deux faces ayant une arête commune ne soient pas de la même couleur[3]. Topologiquement, cet objet est un tore.
Notes et références
- Clifford A Pickover, Le beau livre des maths, Dunod.
- Clifford A Pickover, Le beau livre des maths, Dunod. Citation p 466 : Comme le souligne Martin Gardner << jusqu'à ce que Szilassi ne découvre cette structure, personne ne soupçonnait son existence>>
- Théorème des 7 couleurs
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.