Polynôme de Schur

Les polynômes de Schur sont indexés par les partitions d'entiers ou plus exactement, par les suites finies décroissantes d'entiers naturels. Étant donné un tel n-uplet λ = (λ₁, λ₂, … , λ_n), où les λ_j sont entiers et λ₁ ≥ λ₂ ≥ … ≥ λ_n ≥ 0 (cette suite finie pouvant être vue comme une « partition » de l'entier d = ∑λ_j mais en un sens élargi puisque les derniers λ_j sont autorisés à être nuls), le polynôme suivant est alternant (en), c'est-à-dire qu'il est transformé en son opposé par une transposition des variables :

${\displaystyle a_{\lambda }(x_{1},x_{2},\dots ,x_{n})=\det {\begin{pmatrix}x_{1}^{\lambda _{1}}&x_{2}^{\lambda _{1}}&\dots &x_{n}^{\lambda _{1}}\\x_{1}^{\lambda _{2}}&x_{2}^{\lambda _{2}}&\dots &x_{n}^{\lambda _{2}}\\\vdots &\vdots &\ddots &\vdots \\x_{1}^{\lambda _{n}}&x_{2}^{\lambda _{n}}&\dots &x_{n}^{\lambda _{n}}\end{pmatrix}}.}$

Il est donc divisible par le déterminant de Vandermonde, qui correspond au n-uplet δ = (n – 1, n – 2, … ,0) :

${\displaystyle a_{\delta }(x_{1},x_{2},\dots ,x_{n})=\det {\begin{pmatrix}x_{1}^{n-1}&x_{2}^{n-1}&\dots &x_{n}^{n-1}\\x_{1}^{n-2}&x_{2}^{n-2}&\dots &x_{n}^{n-2}\\\vdots &\vdots &\ddots &\vdots \\1&1&\dots &1\end{pmatrix}}=\prod _{1\leq j<k\leq n}(x_{j}-x_{k}).}$

Le polynôme de Schur associé à λ est par définition[1] le polynôme quotient :

${\displaystyle s_{\lambda }={\frac {a_{\lambda +\delta }}{a_{\delta }}},}$

où les n-uplets λ et δ sont additionnés terme à terme. Il est symétrique, comme quotient de deux polynômes alternants.

Les polynômes de Schur de degré d en n variables forment une base de l'espace des polynômes symétriques homogènes de degré d en n variables.

Pour une partition ${\displaystyle \lambda }$ donnée, le polynôme de Schur ${\displaystyle s_{\lambda }}$ s'écrit aussi comme une somme de monômes, sous la forme :

${\displaystyle s_{\lambda }(x_{1},x_{2},\ldots ,x_{n})=\sum _{T}x^{T}=\sum _{T}x_{1}^{t_{1}}\cdots x_{n}^{t_{n}}}$

où la sommation porte sur les tableaux de Young semi-standard ${\displaystyle T}$ de forme ${\displaystyle \lambda }$ ; les exposants ${\displaystyle t_{1},\ldots ,t_{n}}$ donnent le poids de ${\displaystyle T}$ : en d'autres termes, chaque ${\displaystyle t_{i}}$ compte les occurrences du nombre ${\displaystyle i}$ dans ${\displaystyle T}$. Par exemple, le monôme associé au tableau 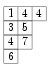est ${\displaystyle x_{1}x_{3}x_{4}^{3}x_{5}x_{6}x_{7}}$.

L'expression comme somme de poids de tableaux de Young est parfois prise comme définition, par exemple dans Sagan 2001.

Les trois tableaux de Young semi-standard de forme ${\displaystyle \lambda =(3,2)}$ et de poids ${\displaystyle \mu =(1,1,2,1)}$. On a donc ${\displaystyle K_{\lambda ,\mu }=3}$.

Les relations avec d'autres bases s'expriment souvent explicitement. Une des bases considérées est celle des fonctions symétriques monomiales ${\displaystyle m_{\mu }}$. Étant donné une partition ${\displaystyle \mu =(\mu _{1},\mu _{2},\ldots ,\mu _{n})}$, le polynôme ${\displaystyle m_{\mu }}$ est par définition[2] :

${\displaystyle m_{\mu }=\sum x_{i_{1}}^{\mu _{1}}x_{i_{2}}^{\mu _{2}}\cdots x_{i_{n}}^{\mu _{n}}}$

où la sommation est sur toutes les permutations ${\displaystyle (i_{1},i_{2},\ldots ,i_{n})}$ des entiers de 1 à ${\displaystyle n}$. Par exemple, pour ${\displaystyle \mu =(2,1,0)}$, on obtient :

${\displaystyle m_{(2,1,0)}=x_{1}^{2}x_{2}+x_{1}^{2}x_{3}+x_{1}x_{2}^{2}+x_{1}x_{3}^{2}+x_{2}^{2}x_{3}+x_{2}x_{3}^{2}}$.

Les polynômes de Schur sont des combinaisons linéaires de polynômes symétriques monomiaux à coefficients entiers naturels notés ${\displaystyle K_{\lambda \mu }}$ et appelés les nombres de Kostka. Le nombre de Kostka ${\displaystyle K_{\lambda \mu }}$ (qui dépend de deux partitions ${\displaystyle \lambda }$ et ${\displaystyle \mu }$) est égal par définition au nombre de tableaux de Young semi-standard de forme ${\displaystyle \lambda }$ et de poids ${\displaystyle \mu }$.

L'expression des polynômes de Schur comme combinaison de polynômes symétriques monomiaux est :

${\displaystyle s_{\lambda }=\sum _{\mu }K_{\lambda \mu }m_{\mu }.\ }$

Les polynômes symétriques homogènes complets

${\displaystyle h_{k}(x_{1},x_{2},\dots ,x_{n})=\sum _{1\leq i_{1}\leq i_{2}\leq \cdots \leq i_{k}\leq n}x_{i_{1}}x_{i_{2}}\cdots x_{i_{k}},}$

c'est-à-dire la somme de tous les monômes de degré ${\displaystyle k}$, en fournissent un autre exemple. Deux formules faisant intervenir des déterminants sont les formules de Jacobi-Trudi[3]. La première exprime les polynômes de Schur comme un déterminant en termes de polynômes symétriques homogènes complets :

${\displaystyle s_{\lambda }=\det _{i,j}h_{\lambda _{i}+j-i}.}$

Pour la partition ${\displaystyle (d)}$ de ${\displaystyle d}$ en une seule part, on a simplement

${\displaystyle s_{(d)}=h_{d}}$.

La dernière relation se comprend facilement. En effet, si la partition comprend un seul terme, les tableaux de Young associés n'ont qu'une seule ligne à ${\displaystyle n}$ cellules, remplies par des entiers qui sont croissants au sens large. Chaque tableau correspond à un terme du polynôme symétrique homogène complet ${\displaystyle h_{d}}$.

La deuxième formule exprime les polynômes de Schur comme un déterminant en termes de polynômes symétriques élémentaires. On note ${\displaystyle e_{k}(x_{1},\ldots ,x_{n})}$ le polynôme symétrique élémentaire qui est la somme des produits distincts de ${\displaystyle k}$ variables distinctes parmi les ${\displaystyle n}$. On a :

${\displaystyle s_{\lambda }=\det _{i,j}e_{\lambda '_{i}+j-i}}$,

où ${\displaystyle \lambda '}$ est la partition duale de ${\displaystyle \lambda }$. Pour la partition ${\displaystyle (1)^{d}}$ dont toutes les parts valent 1, on obtient

${\displaystyle s_{(1)^{d}}=e_{d}}$.

Là également, la dernière formule se comprend bien. Les tableaux de Young sont formés d'une seule colonne de ${\displaystyle n}$ cellules, et les entiers qui y figurent sont strictement croissants. Chaque tableau fournit donc un monôme du polynôme symétrique élémentaire ${\displaystyle e_{d}}$.

Ces formules sont appelées les « identités déterminantales ». Un autre formule de ce type est la formule de Giambelli (en), qui exprime le polynôme de Schur d'une partition en termes de partitions en équerre contenues dans le diagramme de Young correspondant. Dans la notation de Frobenius, la partition est notée

${\displaystyle (a_{1},...a_{r}|b_{1},...b_{r})}$

où, pour chaque élément diagonal, en position ${\displaystyle (i,i)}$, l'entier ${\displaystyle a_{i}}$ est le nombre de cellules à droite et sur la même ligne, et ${\displaystyle b_{i}}$ est le nombre de cellules en dessous et dans la même colonne (respectivement la longueur du « bras » et de la « jambe »).

L'identité de Giambelli exprime la partition comme le déterminant

${\displaystyle s_{(a_{1},...a_{r}|b_{1},...b_{r})}=\det(s_{(a_{i}|b_{j})})}$.

Enfin, l'évaluation du polynôme de Schur ${\displaystyle s_{\lambda }}$ en (1,1,...,1) donne le nombre de tableaux de Young semi-standard de forme ${\displaystyle \lambda }$ avec entrées dans ${\displaystyle \{1,2,\ldots ,n\}}$. On peut montrer, en utilisant par exemple la formule des caractères de Weyl (en), que

${\displaystyle s_{\lambda }(1,1,\dots ,1)=\prod _{1\leq i<j\leq n}{\frac {\lambda _{i}-\lambda _{j}+j-i}{j-i}}.}$

L'exemple qui suit illustre ces définitions. On considère le cas ${\displaystyle n=3,d=4}$. Les partitions de l'entier ${\displaystyle d=4}$ en au plus ${\displaystyle n=3}$ parts sont ${\displaystyle (2,1,1),(2,2),(3,1),(4)}$. On a

${\displaystyle s_{(2,1,1)}(x_{1},x_{2},x_{3})={\frac {1}{\Delta }}\;\det {\begin{pmatrix}x_{1}^{4}&x_{2}^{4}&x_{3}^{4}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}\\x_{1}&x_{2}&x_{3}\end{pmatrix}}=x_{1}\,x_{2}\,x_{3}\,(x_{1}+x_{2}+x_{3})}$

${\displaystyle s_{(2,2,0)}(x_{1},x_{2},x_{3})={\frac {1}{\Delta }}\;\det {\begin{pmatrix}x_{1}^{4}&x_{2}^{4}&x_{3}^{4}\\x_{1}^{3}&x_{2}^{3}&x_{3}^{3}\\1&1&1\end{pmatrix}}=x_{1}^{2}\,x_{2}^{2}+x_{1}^{2}\,x_{3}^{2}+x_{2}^{2}\,x_{3}^{2}+x_{1}^{2}\,x_{2}\,x_{3}+x_{1}\,x_{2}^{2}\,x_{3}+x_{1}\,x_{2}\,x_{3}^{2}}$

et ainsi de suite. La deuxième des formules de Jacobi-Trudi donne les expressions :

1. ${\displaystyle s_{(2,1,1)}=e_{1}\,e_{3}}$
2. ${\displaystyle s_{(2,2,0)}=e_{2}^{2}-e_{1}\,e_{3}}$
3. ${\displaystyle s_{(3,1,0)}=e_{1}^{2}\,e_{2}-e_{2}^{2}-e_{1}\,e_{3}+e_{4}}$
4. ${\displaystyle s_{(4,0,0)}=e_{1}^{4}-3\,e_{1}^{2}\,e_{2}+2\,e_{1}\,e_{3}+e_{2}^{2}-e_{4}.}$

Tout polynôme symétrique homogène de degré 4 en trois variables s'exprime de façon unique comme combinaison linéaire de ces quatre polynômes de Schur. Considérons par exemple le polynôme :

${\displaystyle \phi (x_{1},x_{2},x_{3})=x_{1}^{4}+x_{2}^{4}+x_{3}^{4}}$

C'est bien un polynôme symétrique homogène de degré 4 en trois variables. On trouve :

${\displaystyle \phi =s_{(2,1,1)}-s_{(3,1,0)}+s_{(4,0,0)}.\,\!}$

Les polynômes de Schur interviennent dans la théorie des représentations des groupes symétriques, du groupe général linéaire, et des groupes unitaires. La formule des caractères de Weyl implique que les polynômes de Schur sont les caractères de représentations irréductibles de degré fini des groupes généraux linéaires, et ceci permet de généraliser les travaux de Schur à d'autres groupes de Lie compacts et semi-simples.

Plusieurs expressions sont des conséquences de cette relation. La plus importante est le développement de la fonction de Schur ${\displaystyle s_{\lambda }}$ en termes de sommes de Newton ${\displaystyle p_{k}=\sum _{i}x_{i}^{k}}$. Si l'on note ${\displaystyle \chi _{\rho }^{\lambda }}$ le caractère du groupe symétrique indexé par la partition ${\displaystyle \lambda }$ évalué en des éléments dont le type de cycle est noté par la partition ${\displaystyle \rho }$, alors[4]

${\displaystyle s_{\lambda }=\sum _{\rho =(1^{r_{1}},2^{r_{2}},3^{r_{3}},\dots )}\chi _{\rho }^{\lambda }\prod _{k}{\frac {p_{k}^{r_{k}}}{r_{k}!k^{r_{k}}}},}$

où ${\displaystyle \rho =(1^{r_{1}},2^{r_{2}},3^{r_{3}},\dots )}$ signifie que la partition ${\displaystyle \rho }$ a ${\displaystyle r_{k}}$ parts de longueur ${\displaystyle k}$.

Une fonction de Schur gauche ${\displaystyle s_{\lambda /\mu }}$ dépend de deux partitions ${\displaystyle \lambda }$ et ${\displaystyle \mu }$. Elle peut être définie par la propriété :

${\displaystyle \langle s_{\lambda /\mu },s_{\nu }\rangle =\langle s_{\lambda },s_{\mu }s_{\nu }\rangle .}$

Comme pour les polynômes de Schur ordinaires, il y a diverses façons de les calculer. Les identités de Jacobi-Trudi correspondantes sont :

${\displaystyle s_{\lambda /\mu }=(h_{\lambda _{i}-\mu _{j}-i+j}),1\leq i,j\leq l(\lambda )}$,

${\displaystyle s_{\lambda '/\mu '}=(e_{\lambda _{i}-\mu _{j}-i+j}),1\leq i,j\leq l(\lambda )}$.

Il y a aussi une interprétation combinatoire des polynômes de Schur gauches, à savoir comme somme sur tous les tableaux de Young semi-standard de forme ${\displaystyle \lambda /\mu }$ :

${\displaystyle s_{\lambda /\mu }=\sum x^{T}}$

où la sommation porte cette fois-ci sur les tableaux semi-standard de forme ${\displaystyle \lambda /\mu }$.

• Règle de Littlewood-Richardson, où sont données des identités sur des polynômes de Schur
• Polynômes de Schubert (en), une généralisation des polynômes de Schur