Problème de la chèvre
En mathématiques récréatives, le problème de la chèvre est le nom donné à divers problèmes concernant la superficie qu'une chèvre attachée à un pieu peut brouter en liaison avec la longueur de sa corde, dans diverses situations. On présente ici deux variantes classiques, ayant la particularité rare en mathématiques récréatives d'obliger à résoudre des équations non algébriques, la première demandant de surcroit un calcul d'aire non élémentaire. On trouvera dans les références suivantes de nombreuses autres variantes[1],[2],[3].
Pour les articles homonymes, voir chèvre.
Première variante : chèvre attachée à une tour
Énoncé
Une chèvre est attachée à une tour circulaire (ou un silo) de rayon R située dans un champ. Sachant que sa corde est de longueur L, quelle superficie d'herbe pourra-t-elle brouter ?
Réponse
Si L est inférieure ou égale à , la superficie atteignable vaut .
Pour , il faut retrancher à cette valeur , où , .
Pour une longueur de corde égale à la circonférence de la tour, on trouve par exemple . Cela donne une surface de broutage égale à 76 256 yards carrés pour le problème historique ci-après.

Historique
Ce problème a été publié dans l'édition de 1748 de la revue annuelle anglaise The Ladies' Diary, sous la question CCCIII attribuée à un certain Upnorensis :
Un cheval se trouvant dans un parc, avec l'extrémité d'une corde attachée à son pied avant, et l'autre extrémité à une clôture circulaire métallique entourant un étang de circonférence 160 yards, égale à la longueur de la corde, quelle superficie au plus le cheval peut-il brouter?

Deuxième variante : chèvre pouvant brouter la moitié du pré
Énoncé
Un chèvre étant attachée à un pieu situé à la circonférence d'un pré circulaire de rayon R, quelle doit être la longueur L de sa corde pour qu'elle n'ait accès qu'à la moitié de la surface du pré?
Réponse
où est solution de .
Les décimales de sont données par la suite A133731 de l'OEIS, et celles de par la suite A173201 de l'OEIS.
Historique
Le problème a été publié sans habillage animalier en 1894 dans la première édition de la célèbre revue American Mathematical Monthly. Attribué à Charles E. Myers, il a été rédigé comme suit :
Un cercle renfermant un acre est coupé par un autre dont le centre est sur la circonférence du cercle donné, et l'aire commune aux deux est d'un demi-acre. Trouver le rayon du cercle de coupe.
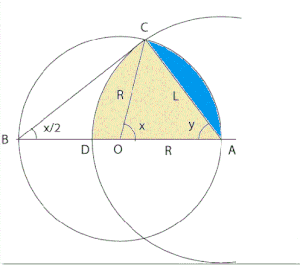
Démonstration trigonométrique
Avec les notations de la figure, l'angle AOC, noté x, est Le double de l'angle ABC, d'après le théorème de l'angle inscrit ; ce dernier vaut donc x/2, et l'angle OAC vaut . L'aire du secteur de cercle ADC vaut donc ; comme , cette aire vaut .
L'aire du segment de disque bleu est égale à l'aire du secteur OAC moins celle du triangle OAC, soit .
L'aire de broutage égale à la moitié de celle du pré s'exprime donc par la relation , laquelle se simplifie en :
, avec .
Posant , on obtient bien :
, avec .
Lien externe
(en) Eric W. Weisstein, « Goat Problem », sur MathWorld, présentant les deux variantes
Références
- Gérard Villemin, « Problème de la chèvre »
- (en) Bassett, « The Goat in the City », The Mathematical Intelligencer, (ISSN 0343-6993, DOI 10.1007/s00283-021-10120-7, lire en ligne)
- Michael E. Hoffman, "The bull and the silo: an application of curvature," American Mathematical Monthly 105 (1998), 55–58
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Goat problem » (voir la liste des auteurs).
- Portail des mathématiques