Problème du diamant
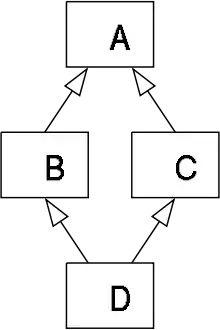
En informatique, le problème du diamant (ou problème du losange dans certains articles scientifiques) arrive principalement en programmation orientée objet, lorsque le langage permet l'héritage multiple. Si une classe D hérite de deux classes B et C, elles-mêmes filles d'une même classe A, se pose un problème de conflit lorsque des fonctions ou des champs des classes B et C portent le même nom. Le nom de ce problème provient de la forme du schéma d'héritage des classes A, B, C et D dans ce cas.
Par exemple, dans le cas d'une interface graphique, une classe Button pourrait hériter de deux classes Rectangle (gérant son apparence) et Clickable (gérant les clics de souris) et ces deux classes hériter d'une classe Object. Si la classe Object définit la fonction equals (gérant la comparaison entre objets), que les deux sous-classes Rectangle et Clickable étendent cette fonction pour l'adapter à leurs particularités, laquelle des fonctions equals de Rectangle ou de Clickable la classe Button doit-elle utiliser ? Choisir arbitrairement une seule des deux fonctions ferait perdre l'intérêt de l'héritage ; utiliser les deux fonctions pose le problème de l'ordre des appels, de la combinaison des résultats (ou des erreurs), de l'éventuelle redondance de leurs effets, etc.
Approches de résolution
En interdisant les homonymies
En C++, ces problèmes sont appelés des ambiguïtés : le compilateur lève une erreur s'il ne parvient pas à déterminer la méthode à utiliser. Le développeur doit alors soit redéfinir la méthode dans la classe dérivée, soit utiliser l'opérateur de résolution de portée (::) pour préciser la méthode à utiliser[1].
Des langages comme Eiffel ou OCaml proposent des constructions plus évoluées pour aider le développeur à résoudre ces ambiguïtés.
En définissant un ordre de priorité
Cela consiste à définir un algorithme de linéarisation pour construire un ordre de résolution des méthodes (MRO : Method Resolution Order). Une bonne linéarisation doit respecter certaines contraintes[2] :
- acceptabilité : elle ne doit dépendre que des déclarations d'héritage, et pas par exemple du nom des classes ;
- priorité locale : elle doit respecter l'ordre des classes parentes qui a été choisi par le programmeur lors de la définition de la classe dérivée ;
- monotonie : si la classe B est avant la classe A dans la linéarisation d'une classe C ([C, B, A, …]), alors la classe B devra être avant la classe A dans la linéarisation de toute classe dérivée de C.
Les langages de programmation peuvent résoudre ce problème de façons différentes :
- Scala utilise la fonction définie dans la première classe, après avoir aplati l'arbre des traits par une recherche « right-first depth-first » et éliminé les doublons (ne conservant que le dernier des traits surnuméraires). Ainsi, l'ordre de résolution de l'exemple de l'introduction serait [D, C, A, B, A], réduit en [D, C, B, A]. Python 2.2 utilisait un algorithme similaire, il a été abandonné car il ne respecte pas la contrainte de monotonie dans certaines situations[3] ;
- Dylan, Perl et Python utilisent l'algorithme C3[4]. Il respecte les trois contraintes d'acceptabilité, de priorité locale et de monotonie ; mais interdit certaines constructions (par exemple E dérivée de C et D si C est dérivée de A et B, et D est dérivée de B et A).
En réservant l'héritage multiple aux interfaces
D'autres langages interdisent plus simplement l'héritage multiple (comme Ada, Ruby, Objective-C, PHP, C#, Delphi/Free Pascal et Java[5]) : une classe n'hérite que d'une seule autre, mais peut implémenter une liste d'interfaces. Ces interfaces ne contiennent que des méthodes abstraites, c'est-à-dire ne contenant aucun code. C'est à la classe d'implémenter toutes les méthodes de toutes ses interfaces. Les interfaces sont dans ce cas assimilables à des contrats forçant toutes les classes les utilisant à implémenter les mêmes méthodes.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Diamond problem » (voir la liste des auteurs).
- (en) « Name Ambiguities », Microsoft Developer Network.
- (en) « A Monotonic Superclass Linearization for Dylan » (version du 15 avril 2012 sur l'Internet Archive), haahr.tempdomainname.com, 28 juin 1996.
- (en) « Method Resolution Order », The History of Python, 23 juin 2010.
- (en) Michele Simionato, « The Python 2.3 Method Resolution Order », Python.org.
- Errata: depuis Java 8, il est possible de simuler un héritage en diamant avec les méthodes
defaultdes interfaces. Ces dernières permettent d'implémenter du code directement dans l'interface, et donc de voir une classe bénéficier de l'implémentation de deux méthodes du même nom dans deux interfaces différentes. Cependant il n'est toujours pas possible d'hériter de deux classes distinctes dans ce langage.
Bibliographie
- Eddy Truyen, Wouter Joosen, Bo Nørregaard Jørgensen, Pierre Verbaeten, « A Generalization and Solution to the Common Ancestor Dilemma Problem in Delegation-Based Object Systems », Proceedings of the 2004 Dynamic Aspects Workshop, nos 103–119, (lire en ligne [PDF])
- Portail de l'informatique théorique