Pyramide de Pascal

En mathématiques, la pyramide de Pascal ou le tétraèdre de Pascal est une généralisation tridimensionnelle du triangle de Pascal. De la même façon que le triangle de Pascal donne les coefficients binomiaux, la pyramide de Pascal donne les coefficients trinomiaux.

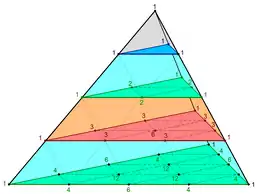
Les 5 premiers niveaux d'une pyramide de Pascal

Coefficients trinomiaux

Présentation et utilité

Les coefficients trinomiaux sont un cas particulier de coefficients multinomiaux, ils s'écrivent sous la forme ${n \choose i,j,k}$ avec $(i,j,k)$ trois entiers naturels (positifs ou nuls) et $n=i+j+k$ . Ils sont définis par la formules ${n \choose i,j,k}={\frac {n!}{i!j!k!}}$ . Comme tous les coefficients multinomiaux, leur intérêt est multiple, on peut les retrouver dans les cas suivants:

En algèbre avec le développement du trinôme de Newton.
En dénombrement, ${n \choose i,j,k}$ est le nombre d'arrangement possible d'une population de n objets composée de i objets d'une espèce A, j objet d'une espèce B et k objets d'une espèce C, les objets d'une même espèce étant indiscernable et leurs positions relatives n'important donc pas.
En statistique, du fait de la propriété précédente.

Lien entre les coefficients trinomiaux et la pyramide de Pascal

La pyramide de Pascal se construit du fait que les coefficients trinomiaux obéissent à une loi de récurrence de type relation de Pascal de la forme: ${n \choose i,j,k}={n-1 \choose i-1,j,k}+{n-1 \choose i,j-1,k}+{n-1 \choose i,j,k-1}$ vrai pour tous triplets $(i,j,k)$ d'entier naturel avec $n=i+j+k$ .

Cette règle reste vrai dans les cas i,j, ou k égal à 0, à condition de prendre la convention suivante: ${n' \choose i',j',k'}=0$ si $i'\leq -1{\text{ ou }}j'\leq -1{\text{ ou }}k'\leq -1{\text{ et }}n'=i'+j'+k'\geq 0$ .

Démonstration

La démonstration consiste à rechercher une factorisation de l'expression

${n-1 \choose i-1,j,k}+{n-1 \choose i,j-1,k}+{n-1 \choose i,j,k-1}={\frac {(n-1)!}{(i-1)!j!k!}}+{\frac {(n-1)!}{i!(j-1)!k!}}+{\frac {(n-1)!}{i!j!(k-1)!}}$

On peut pour cela commencer par mettre le terme (n-1)! en facteur, puis en cherchant à réduire les trois termes aux même dénominateur on va remarquer que ${\frac {1}{(i-1)!}}={\frac {i}{i!}}$ , un dénominateur commun est donc $i!j!k!$

On va donc avoir: ${n-1 \choose i-1,j,k}+{n-1 \choose i,j-1,k}+{n-1 \choose i,j,k-1}={\frac {(n-1)!}{i!j!k!}}\left(i+j+k\right)$

Or $n=i+j+k$ et $(n-1)!n=n!$ donc:

${n-1 \choose i-1,j,k}+{n-1 \choose i,j-1,k}+{n-1 \choose i,j,k-1}={\frac {n!}{i!j!k!}}={n \choose i,j,k}$

Lecture du triangle de Pascal

La pyramide est construite étage par étage en commençant par le sommet (n=0) et en descendant (incrémentation de n). Les premiers étages du haut sont ainsi constitués :

1      1         1              1                   1
     1   1     2   2          3   3               4   4
             1   2   1      3   6   3           6  12   6
                          1   3   3   1       4  12   12  4
                                            1   4   6   4   1

Du fait qu'à l'étage n, les entiers naturel $(i,j,k)$ doivent respecter la relation $n=i+j+k$ , on repère la position du coefficient trinomial ${n \choose i,j,k}$ sur l'étage n à l'aide de conventions telles que celles-ci (appliquée dans ce cas à n=3):

         k=0 
           \
       k=1  1 - j=3 
         \ / \       
     k=2  3 - 3 - j=2 
       \ / \ / \
   k=3  3 - 6 - 3 - j=1
     \ / \ / \ / \ 
      1 - 3 - 3 - 1 - j=0 
     /   /   /   /
   i=0 i=1 i=2 i=3

Ainsi, avec les conventions adoptées, on peut repérer que ${3 \choose 1,1,1}$ est le deuxième coefficients (i=1) présents sur la deuxième ligne (j=1) en partant du bas et est donc égal à 6. De même ${3 \choose 1,2,0}$ est le deuxième (i+1) élément de la troisième (j+1) ligne en partant du bas, il est donc égal à 3, on remarquera que l'élément en question se trouve sur la ligne d'indice k=0.

Le lien avec la relation de Pascal se retrouve du fait que la valeur d'un élément est la somme des trois (deux si on se trouve sur une face, 1 pour une arête) éléments se trouvant directement au-dessus du premier dans l'étage précédent. Par exemple, pour l'étage n=3, le 6 central se trouve être la somme des trois 2 se trouvant juste au-dessus dans l'étage n=2.

Propriétés

Chaque face de la pyramide de Pascal est identifiable au triangle de Pascal. Cela peut être expliqué soit par récurrence, mais il est plus simple de constater qu'une face de la pyramide correspond à un plan vérifiant soit i=0, j=0 ou k=0, et puisque $0!=1$ , on a ${n \choose 0,j,k}={\frac {n!}{j!k!}}={n \choose j,k}$ que l'on peut aussi noter ${n \choose k}$ ou ${n \choose j}$

La pyramide de Pascal peut être utilisée dans le développement du trinôme du newton du fait de la formule:

$(x+y+z)^{n}=\sum _{i,j,k\geq 0,i+j+k=n}{{n \choose i,j,k}x^{i}y^{j}z^{k}}$

On peut déduire de cette formule ou par récurrence que la somme des éléments de l'étage n sera égale à $3^{n}$ .

Une pyramide de Pascal de côté n est constituée de ${\frac {(n+2)!}{6(n-1)!}}$ nombres, la somme de ces nombres est égale à ${\frac {3^{n}-1}{2}}$ .

Un simplexe de Pascal de dimension d et de côté n est constitué de ${\frac {(n+d-1)!}{d!(n-1)!}}$ nombres, la somme de ces nombres est égale à ${\frac {d^{n}-1}{d-1}}$ .

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pascal's pyramid » (voir la liste des auteurs).

Voir aussi

Articles connexes

Liens externes

(en) Beyond Flatland: Geometry for the 21st Century. PART I: Pascal's Tetrahedron
(en) Pascal's Simplices exposés sur le triangle de Pascal, la pyramide de Pascal, et davantage

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.