Quartique de Klein
En géométrie hyperbolique, la quartique de Klein, du nom du mathématicien allemand Felix Klein, est une surface de Riemann compacte de genre 3. Elle a le groupe d'automorphismes d'ordre le plus élevé possible parmi les surfaces de Riemann de genre 3, à savoir le groupe simple d'ordre 168. La quartique de Klein est en conséquence la surface de Hurwitz (en) de genre le plus bas possible.
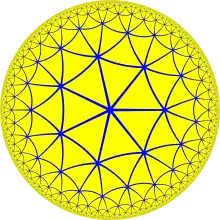
La quartique de Klein est le quotient d'un pavage uniforme triangulaire d'ordre 7.
Voir aussi
Articles connexes
- Surface de Bolza
- Surface de Macbeath
- Premier triplet de Hurwitz (en)
- Théorème de Stark-Heegner
- 56-graphe de Klein
Liens externes
- (en) John Baez, « Courbe quadratique de Klein »,
- (en) Greg Egan, « Courbe quadratique de Klein » (illustrations)
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.