Réflexion d'Andreev
La réflexion d'Andreev (AR), nommée d'après le physicien russe Alexander F. Andreev, est une forme de diffusion de particule qui se produit à l'interface entre un conducteur normal (N) et un supraconducteur (S). C'est un processus de transfert de charge par lequel le courant normal dans N est converti en supercourant dans S. Chaque réflexion d'Andreev transfère une charge 2e à travers l'interface, pour éviter la transmission d'une seule particule, interdite par le gap d'énergie supraconductrice.
Présentation
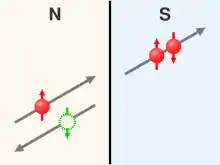
Ce processus implique un électron incident sur l'interface depuis la phase normale, à des énergies plus petites que le gap supraconducteur. L'électron incident forme une paire de Cooper dans le supraconducteur grâce à la rétroréflexion d'un trou de spin et impulsion opposés avec ceux de l'électron incident, comme cela est représenté sur la figure. La transparence de la barrière est supposée importante, sans oxyde ou effet tunnel, qui réduisent les probabilités de diffusion normale électron-électron ou trou-trou à l'interface. Puisque la paire est constituée d'un électron de spin up et d'un électron de spin down, un deuxième électron de spin opposé à celui de l'électron incident est prélevé de la phase normale pour former la paire dans le supraconducteur. Par conséquent, un trou rétroréfléchi est créé dans la phase normale. De plus, grâce à la symétrie de renversement du temps, ce processus décrit pour le cas d'un électron incident fonctionne aussi dans le cas d'un trou incident (et d'un électron rétroréfléchi).
Ce processus est très dépendant du spin : si seulement un des états de spins est occupé par tous les électrons de conduction du matériau en phase normale (c'est-à-dire si le matériau est totalement polarisé), la réflexion d'Andreev va être inhibée à cause de l'impossibilité de former une paire dans le supraconducteur, et par conséquent l'impossibilité de la transmission d'une seule particule. Dans un ferromagnétique ou dans un matériau ou la spin-polarisation existe ou peut être induite par un champ magnétique, l'intensité de la réflexion d'Andreev (et donc la conductance de la jonction) sera une fonction de la spin-polarisation de l'état normal.
Références
Bibliographie
- Livres
- P. G. de Gennes, Superconductivity of Metals and Alloys, New York, W. A. Benjamin, , 274 p. (ISBN 0-7382-0101-4)
- M Tinkham, Introduction to Superconductivity, Second Edition, New York, Dover, (ISBN 0-486-43503-2)
- Articles
- A. F. Andreev, « Thermal conductivity of the intermediate state of superconductors », Sov. Phys. JETP, vol. 19, , p. 1228
- G. E. Blonder, M. Tinkham et T. M. Klapwijk, « Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion », Phys. Rev. B, vol. 25, no 7, , p. 4515 (DOI 10.1103/PhysRevB.25.4515, Bibcode 1982PhRvB..25.4515B)
- M Octavio, M. Tinkham, G. E. Blonder et T. M. Klapwijk, « Subharmonic energy-gap structure in superconducting constrictions », Phys. Rev. B, vol. 27, no 11, , p. 6739 (DOI 10.1103/PhysRevB.27.6739, Bibcode 1983PhRvB..27.6739O)
- M. J. M. de Jong et C. W. J. Beenakker, « Andreev Reflection in Ferromagnet-Superconductor Junctions », Phys. Rev. Lett., vol. 74, no 9, , p. 1657 (PMID 10059084, DOI 10.1103/PhysRevLett.74.1657, Bibcode 1995PhRvL..74.1657D, arXiv cond-mat/9410014)
- R. J. Soulen Jr., J. M. Byers, M. S. Osofsky, B. Nadgorny, T. Ambrose, S. F. Cheng, P. R. Broussard, C. T. Tanaka, J. Nowak, J. S. Moodera, A. Barry, J. M. D. Coey, « Measuring the Spin Polarization of a Metal with a Superconducting Point Contact », Science, vol. 282, no 5386, , p. 85–88 (PMID 9756482, DOI 10.1126/science.282.5386.85, Bibcode 1998Sci...282...85S)
- C. W. J. Beenakker, « Why does a metal-superconductor junction have a resistance? », Quantum Mesoscopic Phenomena and Mesoscopic Devices in Microelectronics, , p. 51–60 (Bibcode 1999cond.mat..9293B, arXiv cond-mat/9909293)
- Portail de la physique