Réseau de neurones de Hopfield

Un réseau de Hopfield à 4 neurones

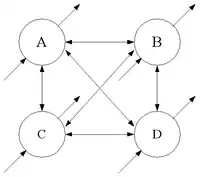
Ce modèle de réseau est constitué de N neurones à états binaires (-1, 1 ou 0, 1 suivant les versions) tous interconnectés. L'entrée totale d'un neurone i est donc :

${\displaystyle I_{i}=\sum _{j}w_{ij}V_{j}}$

où :

• ${\displaystyle w_{ij}}$ est le poids de la connexion du neurone i au neurone j
• ${\displaystyle V_{j}}$ est l'état du neurone j

L'état du réseau peut être caractérisé par un mot de N bits correspondant à l'état de chaque neurone.

Le fonctionnement du réseau est séquencé par une horloge. On notera :

• ${\displaystyle V_{i}(t)}$ ou ${\displaystyle V_{i}}$ l'état du neurone i à l'instant t
• ${\displaystyle V_{i}(t+1)}$ l'état du neurone i à l'instant t + dt où dt désigne l'intervalle de temps entre 2 tops d'horloge

Il existe plusieurs alternatives assez équivalentes pour la mise à jour de l'état des neurones :

• Le mode stochastique original de Hopfield où chaque neurone modifie son état à un instant aléatoire selon une fréquence moyenne égale pour tous les neurones. Plus simplement on peut considérer qu'à chaque top d'horloge, on tire au hasard un neurone afin de le mettre à jour.

• Un mode synchrone où tous les neurones sont mis à jour simultanément.

• Un mode séquentiel où les neurones sont mis à jour selon un ordre défini.

Le calcul du nouvel état du neurone i se fait ainsi :

${\displaystyle V_{i}(t+1)=\left\{{\begin{matrix}1&\mathrm {si} \sum _{j}{w_{ij}V_{j}}>0,\\-1&\mathrm {sinon} \end{matrix}}\right.}$

L'apprentissage dans un réseau d'Hopfield consiste à faire en sorte que chacun des prototypes à mémoriser soit :

• Un état stable du réseau

• Un état attracteur permettant de le retrouver à partir d'états légèrement différents

Pour estimer les poids, on se sert d'un apprentissage hebbien, inspiré de la loi de Hebb (théorisée par Hebb en 1949 et observée réellement dans le cerveau par Bliss et Lomo en 1973). Donc l'une des représentations algébrique est :

${\displaystyle w_{ij}={\frac {1}{n}}\sum _{k=1}^{p}x_{i}^{k}x_{j}^{k}\,}$ ,

où ${\displaystyle w_{ij}}$ est le poids de la connexion entre le neurone ${\displaystyle j}$ et le neurone ${\displaystyle i}$, ${\displaystyle n}$ est la dimension du vecteur d'entrée, ${\displaystyle p}$ le nombre de motif d'entraînement et ${\displaystyle x_{i}^{k}}$ et ${\displaystyle x_{j}^{k}}$ sont respectivement la ${\displaystyle k}$ième entrée des neurones ${\displaystyle i}$ et ${\displaystyle j}$.

L'apprentissage hebbien minimise la fonction d'énergie, c'est-à-dire que si deux unités sont actives simultanément, le poids de leurs connexions est augmenté ou diminué.

Le réseau de Hopfield a cependant des limites bien connues : il ne peut stocker qu'environ 0,14 ${\displaystyle n}$ motifs avec ${\displaystyle n}$ le nombre de neurones. Des modèles ultérieurs, s'inspirant du réseau de Hopfield mais en modifiant les règles de stockage et d'accès, permettent d'agrandir cette limite de stockage[2].