Retour sur trace non chronologique
Dans les algorithmes de recherche et de retour sur trace, le retour sur trace non chronologique ou backjumping est une technique qui réduit l'espace de recherche, et permet donc d'augmenter l'efficacité. En retour sur trace habituel, un retour en arrière remonte d'un niveau dans l'arbre de recherche lorsque toutes les valeurs d'une variable ont été testées. Le retour non chronologique permet de remonter de plusieurs niveaux grâce à une analyse des raisons qui conduisent une combinaison de valeurs pour des variables à échouer. Dans cet article, un ordre fixe de l'évaluation de variables est utilisé, mais les mêmes considérations s'appliquent à une dynamique de l'ordre d'évaluation.
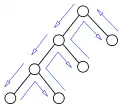 Un arbre de recherche visité régulièrement par les retours en arrière
Un arbre de recherche visité régulièrement par les retours en arrière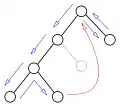 Un backjump: le nœud gris n'est pas visité
Un backjump: le nœud gris n'est pas visité
Définition
Dans un algorithme de retour sur trace, si pour un nœud de l’arbre de recherche si toutes les valeurs de la variable choisies pour ce nœud conduisent à une contradiction, ou encore si aucune valeur de cette variable ne conduit à une solution, l’algorithme revient alors sur la valeur de la variable du nœud parent en tentant une nouvelle valeur, puis à la valeur de la précédente variable si de même toutes les valeurs ont été essayées. Si est l’affectation partielle courante des variables et si toutes les valeurs de ont été essayées sans trouver une solution, l’algorithme conclut qu'aucune pour les valeurs n’existe. Alors l'algorithme « remonte » à , et choisit si possible une nouvelle valeur à affecter à , ou bien retourne de nouveau en arrière s'il n’y a plus de valeur à essayer.
Toutes les valeurs de l’affectation partielle ne sont pas toujours nécessaires pour démontrer qu’aucune valeur de ne permet d'aboutir à une solution. En particulier, un préfixe de l’affectation partielle peut avoir la même propriété, c’est-à-dire qu’il existe un indice tel que ne peut pas être étendue pour former une solution quelle que soit la valeur de . Si l'algorithme peut prouver ce fait, on peut considérer directement une valeur différente pour au lieu de reconsidérer comme il le ferait normalement.
 |
 |
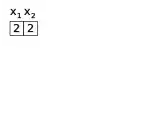 |
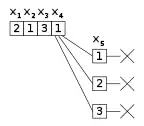
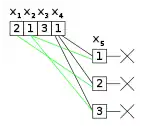
| Un exemple dans lequel l’affectation partielle courante de a été essayée sans succès pour toutes les valeurs possibles de . Le retour sur trace revient sur , en essayant de lui attribuer une nouvelle valeur. | Au lieu de retourner au niveau encore supérieur, l’algorithme élabore en démontrant qu’aucune des affectations , , et | En conséquence, l’affectation de ne conduit jamais à une solution non plus. L’algorithme revient alors directement à , en tentant de lui affecter une nouvelle valeur. |
L'efficacité d'un tel algorithme dépend de la hauteur à laquelle il est capable de remonter non-chronologiquement. Idéalement, l'algorithme pourrait passer de à n’importe laquelle des telle que l'affectation actuelle de ne puisse pas être prolongée pour former une solution pour toute valeur de . Si c'est le cas, est appelé un saut sûr.
Établir si un saut est sûr n'est pas toujours possible, car par définition le démontrer nécessite de connaître l’ensemble des solutions, ce qui est précisément ce qui est cherché par l’algorithme. Dans la pratique, les algorithmes de backjumping ne cherchent pas à trouver tous les sauts surs, mais utilisent des techniques pour démontrer rapidement qu’un saut est sûr. Différents algorithmes utilisent différentes méthodes pour déterminer si un saut est sûr. Le saut effectué est le saut de l’indice le plus bas dont il est efficacement possible de démontrer efficacement sûr. Il y a plusieurs méthodes plus ou moins complexes pour le faire, mais le coût des plus couteuses, si elles permettent de trouver un indice haut, pourrait être compensé par une réduction importante de la taille de l’arbre de recherche. Il y a donc un compromis à trouver.
Backjumping à nœuds feuilles
La plus simple condition sous laquelle le backjumping est possible est lorsque toutes les valeurs d'une variable ont été révélées incompatibles dans un nœud de l’arbre de recherche, et qu’il n’y a donc plus de ramification possible à partir de ce nœud. Dans la satisfaction de contrainte, une affectation partielle est cohérente si et seulement si elle satisfait à toutes les contraintes impliquant les variables assignées, et contradictoire autrement. Il est possible qu’une solution partielle cohérente ne puisse être étendue à une solution plus complète parce qu’assigner des valeurs possibles aux variables supplémentaires conduit systématiquement à générer des évaluations contradictoires.
L'état dans lequel toutes les valeurs d'une variable donnée sont incompatibles avec la solution partielle est appelé une feuille impasse. Cet état survient lorsque la variable est une feuille de l'arbre de recherche (qui correspondent à des nœuds qui ont pour uniques fils une feuille de l’arbre dans les figures de cet article.)
Le backjumping par l'algorithme Gaschnig ne réalise un backjump que dans les feuilles impasses. En d'autres termes, il fonctionne différemment du retour sur trace classique uniquement lorsque toutes les valeurs possibles de x_{k+1} ont été testées et ont engendré une incohérence, sans qu’il ait été nécessaire de ramifier davantage l’arbre.
Un saut sûr peut être trouvé simplement en évaluant, pour chaque valeur le plus court préfixe de incompatible avec . En d'autres termes, si est une valeur possible pour , l'algorithme vérifie la cohérence des évaluations suivantes :
| ... | ||||
| ... | ||||
| ... | ||||
Le plus petit indice (plus bas de la liste) pour laquelle les évaluations sont incohérentes serait un saut sécuritaire dans le cas ou était la seule valeur possible pour . En règle générale il n’y a pas qu’une affectation possible pour une variable, l’indice maximal donné en effectuant cette recherche est par conséquent un saut sûr, et c’est au nœud correspondant que l’algorithme (de Gaschnig) saute.
Sauts vers des nœuds internes
L'algorithme précédent ne saute non chronologiquement que lorsqu'une solution partielle peut être montrée incohérente sans davantage de ramification. En d'autres termes, il ne permet un backjump qu’à des nœuds feuilles de l'arbre de recherche.
Un nœud interne de l'arbre de recherche représente une affectation d'une variable qui est cohérente avec les précédentes. Si aucune solution n’étend cette affectation, l'algorithme précédent saute toujours au nœud parent et jamais non chronologiquement.
Un saut non chronologique vers un nœud interne ne peut être effectué qu’à partir d’une feuille. En effet, si certaines évaluations de nécessitent des ramifications, c'est parce qu'ils sont compatibles avec l'affectation actuelle. En conséquence, la recherche d'un préfixe qui est en contradiction avec ces valeurs potentielles de la dernière variable va échouer.
Dans un tel cas, ce qui a permis de démontrer qu’une affectation ne peut faire partie d’une solution compatible avec l’affectation partielle est la recherche récursive. En particulier, l’algorithme « sait » qu’aucune solution n’est trouvable à partir de ce point parce qu’il est retourné à ce nœud sans avoir trouvé de solution dans un de ses enfants.
Ce retour est causé par un certain nombre d’impasses, des points où l’algorithme a démontré qu’une certaine affectation partielle est incohérente. Pour sauter plus haut, l’algorithme doit prendre en compte le fait que l’impossibilité de trouver des solutions est causée par ces impasses. En particulier, les sauts surs sont les index des préfixes qui préservent le fait que les affectations partielles de ces impasses soient également des affectations partielles incohérentes.
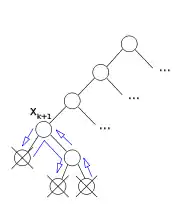 |
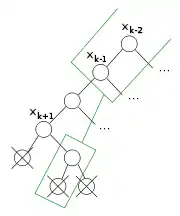 |
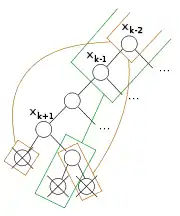 |
 |
|
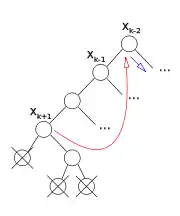
| Dans cet exemple, l’algorithme retourne à , après avoir testé toutes les valeurs possibles. En effet, tous les points qu’il a croisés étaient incohérents. | Le second point demeure incohérent quand les valeurs pour et sont supprimées de l’affectation partielle (noter que les valeurs d’une variables sont dans les enfants de son nœud) | Les autres évaluations incohérentes le restent également en retirant , , et | L’algorithme peut sauter vers car c’est la variable la plus basse dans l’arbre qui conserve toutes les incohérences. Une nouvelle valeur de sera essayée. |
En d’autres termes, lorsque toutes les valeurs de ont été testées, l’algorithme peut faire un saut vers une variable précédente à partir du moment ou la valeur de vérité de l’évaluation partielle de des nœuds feuilles descendants de . est fausse.
Simplifications
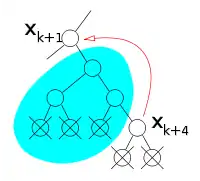
De par le nombre potentiellement important de nœuds dans le sous-arbre de , l’information nécessaire pour sauter non chronologiquement de manière sure depuis est collectée pendant l’exploration de ses sous-arbres. Il est possible d’optimiser la recherche d’un saut sûr de deux manières. La première est que l’algorithme fonctionne pour n’importe quel saut sûr, par conséquent il n’est pas nécessaire de trouver le saut le plus haut possible.
La seconde est que les nœuds du sous-arbre de évités lors d’un saut peuvent être ignorés lorsqu’on cherche un saut pour . Plus précisément, tous les nœuds évités lors d’un saut d’un nœud vers un nœud sont non pertinents pour le sous arbre enraciné en , et ainsi que leurs sous-arbres.
En effet, si un nœud descend d’un nœud x_{l} via un chemin, et qu’un saut non chronologique a lieu lors du retour vers x_l, il aurait été possible de raccourcir ce chemin et d’aller directement de à et d’obtenir le même résultat. Le saut nous indique que les affectations des nœuds entre et sont non pertinentes pour le sous-arbre enraciné en . En d’autres termes, un saut non chronologique indique que visiter une région de l’arbre de recherche était une erreur. Cette partie peut donc être ignorée quand on évalue l’opportunité d’un saut non chronologique depuis ou l’un de ses ancêtres.
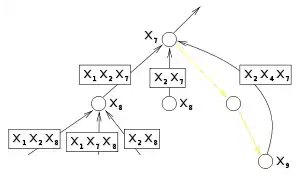
Ce fait peut être exploité en collectant dans chaque nœud un ensemble de variables assignées précédemment dont l’évaluation est suffisante pour montrer qu’aucune solution n’existe dans le sous-arbre enraciné à ce nœud. Cet ensemble est construit pendant l’exécution de l’algorithme. Lors d’un saut depuis d’un nœud, la variable de ce nœud en est retirée et rajoutée à l’ensemble associé à la destination du saut. Comme on ne saute jamais depuis un nœud évité par un saut non chronologique, leurs ensembles sont ignorés automatiquement.
Trouver les sauts avec des graphes
La recherche de sauts non chronologiques à l’aide de graphe a été introduite car un saut sûr peut être trouvé en vérifiant lesquelles des variables apparaissent dans une contrainte contenant des variables qui sont instanciées dans les nœuds feuilles. Pour chaque nœud feuille et chaque variable d'indice instancié à ce nœud, les indices inférieurs ou égaux à dont la variable est dans une contrainte avec peuvent être utilisés pour trouver des sauts sûrs. En particulier, lorsque toutes les valeurs pour ont été tentées, cet ensemble contient les indices des variables dont les évaluations permettent de prouver qu'aucune solution ne sera trouvée en visitant le sous-arbre enraciné au nœud . En conséquence, l'algorithme peut sauter à l'indice le plus élevé dans cette série.
Le fait que les nœuds ignorés par saut non chronologique peuvent être ignorés lors de la recherche ultérieure d’un autre saut peut être utilisé en exploitant l’algorithme suivant. Lors de la rétraction à partir d'un nœud feuille, un ensemble de variables qui sont dans une contrainte de sa variable est créé et « renvoyé » à son père, ou ancêtre en cas de saut non chronologique. Un ensemble de variables est maintenu dans chaque nœud interne. Chaque fois qu'un ensemble de variables est reçu d'un de ses enfants ou descendants, leurs variables sont ajoutées à l’ensemble de ce nœud. Lors d’un saut à partir de ce nœud, son ensemble, duquel on aura retiré la variable du nœud, est envoyé au nœud de destination. Cet algorithme fonctionne parce que l’ensemble maintenu dans un nœud recueille toutes les variables qui sont pertinentes pour prouver l’incohérence des feuilles qui en descendent. Ces ensembles de variables n’étant transmis que lors d’un saut depuis un nœud, les ensembles collectés au niveau des nœuds évités lors d’un saut sont automatiquement ignorés.
Les sauts dirigés par les conflits
Un algorithme de saut non chronologique encore plus raffiné, parfois en mesure d’éviter l’exploration de davantage de nœuds, est fondé sur l’analyse de la contrainte qui a causé l’incohérence, et plus seulement sur la présence de deux variables dans une même contrainte. En particulier, cet algorithme recueille l'une des contraintes violées dans chaque feuille. À chaque nœud l'indice le plus élevé parmi les variables apparaissant dans une contrainte collecté dans les feuilles est un saut sûr.
Quelle que soit la contrainte violée choisie dans chaque feuille, le saut est sûr. En choisissant les contraintes possédant les indices les plus hauts on maximise donc la hauteur du saut. Pour cette raison, les algorithmes à sauts dirigés par conflits ordonnent les contraintes de manière que les contraintes avec des variables de bas indices soient préférées aux contraintes avec des variables d’indices plus hauts.
Formellement, une contrainte est préférée à un autre si l'indice le plus élevé d'une variable dans mais pas dans est inférieur à l'indice le plus élevé d'une variable dans mais pas dans . En d'autres termes, à l'exclusion des variables communes, la contrainte qui possède les variables de plus bas indice est préférée.
Dans un nœud feuille, l'algorithme choisit le plus petit indice tel que entraîne une incohérence avec l’affectation de la variable de la feuille. Parmi les contraintes qui sont violées par cette affectation, il en choisit une d’après l’heuristique qui vient d’être décrite, et recueille les indices de ses variables inférieures à . De cette façon, lorsque l'algorithme revient à la variable l’indice collecté le plus bas dénote un saut sûr.
Dans la pratique, cet algorithme est simplifié par la collecte de tous les indices dans un seul ensemble, au lieu de créer un ensemble pour chaque valeur de . En particulier, l'algorithme collecte, dans chaque nœud, tous les ensembles qui reviennent de ses descendants qui n'ont pas été ignorés par saut non chronologique. Lors d’un retour à partir de ce nœud, son ensemble retranché de sa variable est ajouté à l’ensemble du nœud de destination du retour.
Voir aussi
- Retour sur trace
- Apprentissage de contraintes (en)
Références
- Rina Dechter, Constraint Processing, Morgan Kaufmann, , 481 p. (ISBN 1-55860-890-7, lire en ligne)
- Patrick Prosser, « Hybrid Algorithms for the Constraint Satisfaction Problem », Computational Intelligence, (lire en ligne)
- Portail de l’informatique
- Portail de l'informatique théorique