Pierre-papier-ciseaux
Pierre-papier-ciseaux est un jeu effectué avec les mains et opposant deux joueurs. Il possède de nombreux noms alternatifs, notamment en variant l'ordre des termes ou en remplaçant certains mots comme « papier » par « feuille » ou « pierre » par « caillou » ou « roche ». Le terme chifoumi est également une appellation courante.
jeu de société
| Autre nom |
Papier-ciseaux-caillou |
|---|---|
| Format | Mains des joueurs |
| Mécanismes |
Choix simultané Intuition |
| Joueur(s) | 2 |
| Durée annoncée | 3 secondes |
| habileté physique | réflexion décision | générateur de hasard | information |
D'autres noms existent en fonction des variantes du jeu.
Déroulement du jeu
Les deux joueurs choisissent simultanément un des trois coups possibles en le symbolisant de la main :
.png.webp) |
.png.webp) |
.png.webp) | ||
Pierre. |
Papier. |
Ciseaux. |
De façon générale, la pierre bat les ciseaux (en les émoussant), les ciseaux battent la feuille (en la coupant), la feuille bat la pierre (en l'enveloppant). Ainsi chaque coup bat un autre coup, fait match nul contre le deuxième (son homologue) et est battu par le troisième.
Histoire
%252C_Japanese_rock-paper-scissors_variant%252C_from_the_Kensarae_sumai_zue_(1809).jpg.webp)

Tout comme le jeu de go et le mahjong, le jeu des trois coups fut inventé en Chine. Selon un livre nommé Wuzazu (zh) (五杂组 / 五雜組, ou 五雜俎) écrit par Xie Zhaozhi (zh) (谢肇淛 / 謝肇淛, ) vers la fin de la période Ming, les seigneurs de la dynastie Han jouaient à un jeu (dans lequel le perdant est obligé de boire) appelé shǒushìlìng (手勢令, , « jeu des signes des mains »). Celui-ci est considéré comme étant le jeu des trois coups. Le premier usage de la pierre, de la feuille et des ciseaux comme les trois coups apparaît au Japon au cours du XVIIe siècle[1].
Il n'y a aucune trace de pierre-feuille-ciseaux en Occident avant qu'il n'y ait de contacts directs avec l'Asie. Les auteurs occidentaux de la fin du XIXe siècle l'ont seulement mentionné comme un jeu asiatique. Les Chinois et les Coréens utilisent le tissu avec la pierre et les ciseaux, alors que les Japonais utilisent la feuille. D'ailleurs l'introduction aux États-Unis était très tardive[2] même s'il y avait déjà des coolies chinois. Ceci nous permet de supposer que ce jeu est arrivé en Occident au contact du Japon. Par ailleurs, une variante du nom de ce jeu, chifoumi ou shifumi[3], est sans doute issue du japonais Hi-fu-mi (一二三, les ordinaux 1er, 2e et 3e). Notons toutefois que le jeu de la mourre, autre jeu de doigts reposant sur l'affrontement réflexe entre deux adversaires, est très anciennement connu en Occident.
Stratégie et hasard

La variante solitaire consistant à jouer contre une machine utilisant la stratégie optimale constitue un jeu de hasard pur. Pierre-feuille-ciseaux ne peut donc pas, à proprement parler, être classé comme jeu de hasard raisonné. Cette catégorie de jeux concernant plutôt les jeux à information non complète, fondés sur les probabilités, où des éléments tangibles permettent de favoriser tel comportement au lieu d'un autre.
Dans la variante à trois choix, la stratégie optimale, au sens de la théorie des jeux, consiste à choisir les coups de façon aléatoire, de manière équiprobable. Cependant, il ne s'agit là que de la stratégie garantissant qu'il n'existe pas de stratégie de l'adversaire lui permettant de gagner avec une probabilité strictement supérieure à 1⁄3. Face à un adversaire pratiquant une stratégie sous-optimale, il est possible de trouver des stratégies gagnantes, basées sur la connaissance de l'adversaire.
De nombreuses expériences suggèrent qu'il est quasi impossible à un humain de générer une séquence aléatoire sans l'aide d'un générateur aléatoire (dé, pièce de monnaie, etc.) ou pseudo-aléatoire (programme informatique, liste des décimales de π, etc.). Partant de ce constat, des joueurs essaient de comprendre les séquences de leur adversaire humain pour s'y opposer. Cela revient à jouer de manière « psychologique », en tentant d'anticiper les choix de son adversaire si on a cru percevoir une certaine logique dans son jeu, comme au poker par exemple. Mais en choisissant cette façon de jouer, si on est presque certain de s'éloigner des 33,33 % de gains aléatoires, on n'est absolument pas assuré de s'en éloigner dans le bon sens. Car en essayant de contrer la logique d'un adversaire, le joueur en adopte une lui-même, que son adversaire peut mettre à son profit à son tour. La meilleure méthode pour s'opposer à un adversaire qui essaie de comprendre ses séquences consiste à jouer effectivement le plus au hasard possible, puisque c'est la meilleure façon de rester impénétrable pour son adversaire.
Les théoriciens du pierre-feuille-ciseaux estiment donc que les meilleurs joueurs sont ceux qui, plutôt que de chercher à percer la logique de leur adversaire, restent suffisamment concentrés pour enlever toute apparence logique à leurs choix et se rapprocher du hasard.
« Triche » robotique
Des chercheurs du laboratoire Ishikawa Oku de l'université de Tokyo ont réussi à fabriquer un robot battant systématiquement un joueur humain au jeu pierre-feuille-ciseaux. Il s'agit d'une application des techniques de « reconnaissance d'intention », où le robot « triche » en observant le mouvement de la main de son adversaire et en prenant sa décision très rapidement en fonction de ce mouvement[4].
Pseudo-fédérations
De nombreux sites web affirment organiser des événements imitant les grandes compétitions sportives sans qu'il soit réellement possible d'estimer leur ampleur réelle.
La seule organisation dont l'existence réelle soit établie est la société internationale du RPS (World RPS society) basée à Toronto qui dit compter environ 350 membres. Elle organise un tournoi onéreux et richement doté, qu'elle intitule « championnat du monde ». En 2003, ce tournoi a réuni plusieurs centaines de participants espérant toucher le gros lot ainsi que quelques spectateurs de l'agglomération torontoise. Le tournoi a attiré l'attention des médias[5]. Il suffit cependant de consulter le site de cette organisation pour comprendre qu'il s'agit d'une parodie de fédération sportive.
Variantes
| Région | A | B | C | D | E |
|---|---|---|---|---|---|
| Pierre | Ciseaux | Emballage | |||
| Pierre | Ciseaux | Emballage | Puits | ||
| Puits | Ciseaux | Papier | |||
| Pierre | Papier | Ciseaux | |||
| Pierre | Papier | Ciseaux | Puits | ||
| Pierre | Papier | Ciseaux | Baguette Magique | ||
| Pierre | Papier | Ciseaux | Lézard | Spock | |
| Roche | Papier | Ciseaux | |||
| Roche | Papier | Ciseaux | Mèche | ||
| Roche | Papier | Ciseaux | Dynamite | ||
| Roche | Papier | Ciseaux | Cigarette | ||
| Roche | Papier | Ciseaux | Allumette | ||
| Roche | Papier | Ciseaux | Allumette | Canal | |
| Roche | Papier | Ciseaux | Allumette | Puits | |
| Roche | Papier | Ciseaux | Allumette | Bol de toilette | |
| Pierre | Ciseaux | Emballage | |||
| Marteau | Ciseaux | Papier | |||
| Corée | Pierre | Ciseaux | Emballage | ||
| Pairs (odds) | Impairs (evens) | ||||
| Pierre | Feuille | Ciseaux | |||
| Pierre | Feuille | Ciseaux | Lézard | Serpent | |
| Pierre | Feuille | Ciseaux | Lézard | Spock | |
| Caillou | Ciseaux | Papier | |||
| Pierre | Feuille | Ciseaux | Puits | Bombe | |
| Pierre | Feuille | Ciseaux | Galaxie | Acarien | |
| Pierre | Feuille | Ciseaux | Puits | ||
| Pierre | Feuille | Ciseaux | Spock | Jabba | |
| Écureuil | Gland | Fusil | |||
| Feu | Eau | Feuille | |||
| Pierre | Feuille | Ciseaux | Puits | Volcan | |
| Éléphant | Être humain | Fourmi | |||
| Pierre | Ciseaux | Papier | |||
| Pierre | Ciseaux | Emballage | |||
| Serpent | Grenouille | Limace | |||
| Guerrier | Tigre | Mère du guerrier | |||
| Chef de village | Tigre | Mère du chef de village | |||
| Feu | Serpent | Eau | |||
| Pistolet | Oiseau | Eau | |||
| ( |
Puits | Ciseaux | Feuille | ||
| Pierre | Ciseaux | Feuille | |||
| Général | Fusil | Main levée | |||
| Pierre | Ciseaux | Papier | |||
| Pierre | Ciseaux | Sac | |||
| Papier | Caillou | Ciseaux | chocolat | ||
| Caillou | Ciseaux | Feuille | Puits | Bougie | |
| Pierre | Ciseaux | Feuille | |||
| Pierre | Papier | Ciseaux | |||
| Marteau | Ciseaux | Papier | |||
| Marteau | Ongle | Emballage | |||
| Puits | Ciseaux | Feuille | |||
Dans certaines de ces variantes, de nouveaux symboles apparaissent : comme le puits bat la pierre ainsi que les ciseaux (en les faisant tomber au fond), et est battu par la feuille (qui le recouvre). La probabilité de victoire inégale entre les symboles fait du jeu un exercice psychologique. Il s'agit de prévoir la préférence de son adversaire, et de choisir un symbole qui la bat.
Afin de garder une probabilité de victoire égale entre chaque objet pour conserver un jeu de pur hasard, un cinquième objet, la bombe a été créée. Elle fait exploser le puits et brûle la feuille, mais les ciseaux coupent la mèche et la pierre ne craint rien. Donc chaque objet gagne contre 2 et perd contre les 2 autres. Elle se représente avec le poing fermé et l'index levé pour la mèche.
D'autres variantes sont possibles. L'une des autres variantes est celle des 3-3 : Le jeu se joue par manches. Le gagnant est le premier des joueurs à atteindre 3 victoires. Il y a six actions possibles : les trois basiques (la pierre, les ciseaux ainsi que la feuille), ainsi que trois bonus. Les bonus sont le puits, le super-puits, et la super-pierre. Ceux-ci ne sont utilisables qu'une seule fois par manche et par joueur. Ils fonctionnent ainsi : La super-pierre bat tout (y compris le puits et le super-puits), sauf la feuille, qui l'enveloppe. Le super-puits bat également tout (y compris la feuille et le puits, qui tombent dedans : le super-puits est en effet très grand) sauf la super-pierre. Pour ce qui est du puits, il fonctionne normalement : il ne bat que la pierre et les ciseaux. Le gagnant est le premier à remporter 3 victoires.
Il est aussi possible d'associer perdant et 3-3, en obligeant chaque joueur à utiliser une fois chacun des Bonus. Cette variante se joue en sept duels. Le gagnant est celui qui en a gagné le moins.
Une nouvelle variante a été popularisée par la série américaine The Big Bang Theory[6], mais originellement créée par Sam Kass et Karen Bryla [7]. Il s'agit de Pierre-Papier-Ciseaux-Lézard-Spock. Ici, les règles classiques s'appliquent, mais il faut ajouter que le lézard mange le papier, empoisonne Spock, est écrasé par la pierre et est décapité par les ciseaux. Spock vaporise la pierre, casse les ciseaux, et est discrédité par le papier. Cette variante augmente le nombre de combinaisons de 3 à 10, et est censée réduire le nombre d'égalités entre deux joueurs qui se connaissent (bien qu'entre les personnages de la série, cette variante amène systématiquement à une égalité Spock vs. Spock).
Une autre variante, française, a été popularisée par le jeu Le Tout (inventé par les Tobiffleurs). Il s'agit de Pierre-Feuille-Ciseaux-Galaxie-Acarien. Ici, on reprend les règles classiques en ajoutant la galaxie qui dématérialise la pierre, la feuille et le ciseau, mais implose à cause de l’acarien. L’acarien se fait écraser par la pierre, la feuille et le ciseau.
Il existe aussi des versions de chifoumi en jeu de plateau[8]. PIPACI[9] est un jeu de pions original avec un déplacement et un système de prise assez déroutant.
Une autre variante japonaise est celle du Pierre-Feuille-Ciseaux à contrainte qui ne se joue que sous forme de tournoi et à plus de 6 joueurs ; contrairement aux autres variantes, il ne se joue pas avec des signes reproduits avec les mains mais avec des cartes. Chaque joueur possède 9 cartes : 3 pierres, 3 feuilles et 3 ciseaux. Il possède aussi 3 insignes (peu importe leurs forme, il faut savoir que ce sont des insignes). Le déroulement est le suivant : chaque joueur va aller affronter les autres joueurs un par un lors d'un pierre-feuille-ciseaux classique mais avec comme objectif de finir après le nombre de parties qu'il veut avec aucune carte et minimum 3 insignes. Avant chaque manche, on mise un nombre d'insignes qui doit être le même pour chaque participant. Chacun pose alors sa carte face cachée, puis la retourne en même temps que son adversaire ; s'il y a égalité, les joueurs récupèrent leurs insignes et peuvent décider d'un commun accord de rejouer ou bien aller jouer contre quelqu'un d'autre. Celui qui perd donne le nombre d'insignes misés à son adversaire, celui qui gagne récupère donc les insignes. Chaque carte, dès lors qu'elle est utilisée, est jetée dans une urne et n'est plus utilisable. Les échanges de cartes et d'insignes sont autorisés. Cette variante est sûrement l'une des plus stratégiques de toutes puisqu'elle propose aux joueurs de nombreux moyens d'élaborer des techniques, comme tenter de racheter toutes les cartes pierres ou autres.
Les règles du duel d'ombrelles, un jeu steampunk, se calquent sur celles de pierre-papier-ciseaux.
Nombre de signes
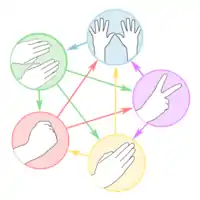
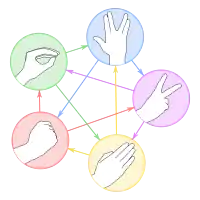
La forme la plus simple du jeu est celle donnée dans le titre, à trois symboles. C'est le minimum pour que chaque symbole soit vainqueur ou perdant face aux symboles opposés différents.
Les joueurs peuvent être tentés de rajouter des symboles pour rendre le jeu plus subtil. Toutefois, le choix de quatre symboles ne fonctionne pas. En effet, si l'on prend l'exemple de Pierre-Feuille-Ciseaux-Puits : le puits et la feuille l'emportent dans deux cas sur quatre tandis que la pierre et les ciseaux seulement une fois sur quatre. Cependant, les ciseaux sont les seuls à l'emporter sur la feuille ; et comme par ailleurs, entre la pierre et le puits, chacun des deux a les mêmes résultats contre feuille et ciseaux, mais que puits l'emporte sur pierre, l'équilibre de Nash du jeu consiste à ne jamais jouer pierre, et à faire comme si le jeu était puits-feuille-ciseaux.
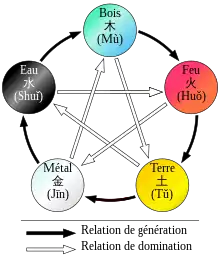
Plus généralement, toute variante avec un nombre pair de symboles conduit, soit à avoir des symboles plus puissants que d'autres (on a vu plus haut une variante pour laquelle cela est compensé par le fait qu'on a le droit de ne jouer qu'une seule fois les symboles surpuissants), ou à avoir des cas de nullité alors que les symboles sont différents.
Au contraire, on a vu que dans la variante à cinq symboles de Kass et Bryla, l'équilibre est préservé : chaque choix peut permettre de perdre ou gagner contre deux autres items. Il existe ainsi (2 parmi 5) combinaisons possibles contre seulement (2 parmi 3) combinaisons. De plus, chaque symbole est ainsi réellement unique.
Une telle relation à cinq, chacun étant dominé par deux autres et dominant deux autres, se trouvait déjà dans le Wuxing chinois, les cinq éléments.
Médias
En 2005, le président d'une grande entreprise japonaise a fait jouer à ce jeu les représentants de Christie's et de Sotheby's pour décider laquelle des deux maisons pourrait organiser la vente d'une collection de tableaux impressionnistes appartenant à sa société et qui comptait notamment un Picasso, un Cézanne et un Van Gogh. Les ciseaux de Christie's ont battu le papier de Sotheby's[10]. Il existe aujourd'hui, un jeu en ligne reproduisant le jeu du pierre feuille ciseaux sous le nom de chifoumi.io.
Références culturelles
Un roman de Henri Troyat porte le titre de La Pierre, la Feuille et les Ciseaux (1972).
Dans le manga Dragon Ball, Son Goku utilise la technique du pierre-ciseaux-papier, dont chaque élément est en fait un coup contre l'adversaire : la pierre est un simple coup de poing, les ciseaux sont deux doigts dans les yeux, et le papier un coup avec la paume de la main.
Dans le shōnen manga Hunter X Hunter, le Hatsu de Gon repose sur le style du pierre-papier-ciseau :
- pierre : Gon donne un coup de poing amplifié par son aura.
- papier : Gon projette son aura par la paume.
- ciseau : Gon produit une lame d'aura avec son index et son majeur.
Le jeu vidéo Alex Kidd in Miracle World met en scène le jeu pierre-feuille-ciseaux à plusieurs reprises : le joueur doit en effet gagner à ce jeu pour vaincre les différents boss qui ponctuent son parcours. Le boss de fin s'appelle d'ailleurs Janken le grand, jan-ken étant le nom japonais du pierre-feuille-ciseaux. champion du monde en titre : Rigonnaux manu (corse)[réf. nécessaire][Quand ?]
Dans le roman policier de Dominique Sylvain, Kabukichō, une scène décrit le déroulement de ce jeu[11].
Théorie des jeux et intelligence artificielle
Le théorème du minimax de von Neumann assure, quel que soit le nombre d'objets, les règles de dominations et les gains (dès lors que le jeu est à somme nulle), l'existence d'une stratégie mixte (c'est-à-dire, des fréquences de jeu des différents objets) optimale. Cet équilibre Min-max est aussi un équilibre de Nash. Par exemple, dans le jeu pierre-papier-ciseaux-puits, l'équilibre correspond à la stratégie où l'on ne joue jamais la pierre, et on joue les trois autres symboles avec la même probabilité 1⁄3. Dans le cas standard où les enjeux sont -1 ou +1, on a ce qu'on appelle un jeu de tournoi et on peut démontrer que l'équilibre est unique[12].
Par delà ces propriétés mathématiques, ce jeu pose d’intéressants problèmes tant en termes d'intelligence artificielle que d'étude du cerveau. En effet, un joueur humain ne joue jamais de façon parfaitement aléatoire et des programmes informatiques sont capables de s'adapter au comportement d'un joueur humain pour gagner[13].
Notes et références
- Linhart, Sepp (1995). Rituality in the ken game. Ceremony and Ritual in Japan. London: Routledge. p. 38–41. (ISBN 9780415116633).
- (en) Marion May Dilts, « COMMUTING WITH TOKYO'S SUBURBANITES; Their Morning Ritual Is Characteristically Japanese, but In Their Mode of Travel There Is Western Technique », New York Times, .
- « Tous les jeux de mains », sur editions-larousse.fr.
- Chloé Durand-Parenti, « Un robot imbattable au chifoumi », sur Le Point.fr, .
- « L'annonce du « championnat du monde » 2009 », sur Lemonde.fr, .
- The Times y fait référence dans cet article antérieur à la série : (en) « … and paper scissors ».
- (en) Sam Kass, « Page originale Rock-Paper-Scissors-Spock-Lizard » (consulté le ).
- Jeu de plateau Chifoumi.
- Jeu de plateau original PIPACI.
- Carol Vogel, « Rock, Paper, Payoff: Child's Play Wins Auction House an Art Sale », sur New York Times, .
- Syvain, Dominique (2016). Kabukichō. Paris, Point Seuil. (p. 172). (ISBN 9782757867860).
- (en) Jean-François Laslier, Tournament Solutions and Majority Voting, Springer-Verlag, .
- Fabrice Rossi, « L'ordinateur peut-il lire dans votre esprit ? » [PDF], sur apiacoa.org, .
Annexes
Articles connexes
- Paradoxe de Condorcet
- Paradoxe de Penney
- Théorème du minimax de von Neumann (le jeu de pierre-feuille-ciseaux est étudié dans cet article comme exemple de jeu à somme nulle)
- Roche Papier Ciseaux, film québécois
Liens externes
- Portail des jeux