Set!

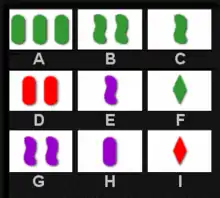
Le jeu est constitué de 81 cartes toutes différentes qui se distinguent selon 4 caractéristiques :

• Nombre : 1, 2 ou 3
• Couleur : rouge, violet ou turquoise
• Forme : ovale, rectangle ou vague (losange, rectangle arrondi ou vague dans la version originale)
• Contenu : vide, hachuré ou plein

Trouver le maximum de sets. Un set est composé de trois cartes dont les quatre caractéristiques (prises séparément) sont :

• soit totalement identiques (par exemple les trois cartes ont la même couleur),
• soit totalement différentes (par exemple chacune des trois cartes est d'une couleur différente).

Une partie de Set!

Les 81 cartes sont mélangées. On tire 12 cartes et on les dispose en "3x4". Tout le monde joue en même temps. Le premier joueur qui voit un set dit « Set ! » et le montre aux autres. Si le set est bon, le joueur prend les trois cartes et les garde dans sa pile de gain. On complète avec trois cartes de la pioche. S'il n'est pas bon, le jeu continue mais celui qui s'est trompé doit attendre qu'un autre joueur trouve un set avant de pouvoir rejouer.

Si aucun set ne figure parmi les 12 cartes, on ajoute 3 cartes, mais on ne complètera pas après qu'un joueur a trouvé une solution.

Le jeu est fini quand toutes les cartes ont été tirées et qu'il n'y a plus de set dans celles qui restent. Le gagnant est celui qui a le plus grand nombre de sets.

Quelques propriétés combinatoires :

• Pour chaque paire de cartes, il existe une et une seule troisième carte pour compléter un set.
• Le plus grand nombre de cartes que l'on peut poser sans qu'un set soit possible est de 20. Voir sur le site officiel en anglais.
• La probabilité de tirer un ensemble de 20 cartes données est

${\displaystyle {\frac {1}{81 \choose 20}}={\frac {20!61!}{81!}}=2.1302\times 10^{-19}}$

(Ce qui est égal à : ${\displaystyle \left({\frac {20}{81}}\right)\left({\frac {19}{80}}\right)\left({\frac {18}{79}}\right)\cdot \cdot \cdot \left({\frac {1}{62}}\right)={\frac {20!61!}{81!}}=2.1302\times 10^{-19}}$.)

• Quand on fait une partie de Set! normale (sans ramasser accidentellement un set incorrect), il est impossible que le jeu se termine avec 3 cartes qui ne constituent pas un set. En d'autres termes, si les 81 cartes de Set! sont réparties en 27 paquets de 3 cartes et que 26 paquets constituent des sets, alors le dernier paquet est obligatoirement un set.

Le jeu possède plusieurs aspects mathématiques intéressants[1].

• Mensa Select Mind Games 1991

Marsha Falco a été récompensée deux fois par le Mensa Select : pour Set! en 1991 et pour Quiddler en 1999.

• quelques réflexions sur le nombre minimum de cartes nécessaires pour contenir un set
• (en) Les jeux de Marsha Falco sur Luding

Ci-dessous se trouvent les solutions du problème posé en haut de page. Ne lisez pas ceci avant d'avoir essayé de résoudre ce problème.

1. A B F : nombres et formes différents, couleurs et remplissages identiques
2. A D H : nombres et couleurs différents, formes et remplissages identiques
3. A G I : nombres, formes et couleurs différents, remplissages identiques
4. C H I : formes et couleurs différentes, nombres et remplissages identiques

• Portail des jeux