Sinus verse

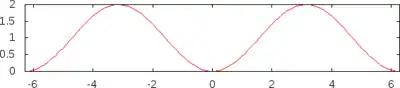
Le sinus verse est une fonction trigonométrique peu utilisée de nos jours. Elle est généralement notée versin, vers ou encore sin v. et définie comme :

${\displaystyle {\textrm {versin}}(\theta )=1-\cos(\theta )=2\sin ^{2}\left({\frac {\theta }{2}}\right).}$

le sinus verse de l'angle θ correspond à la longueur du segment CD, c'est la flèche de l'arc AB

La fonction sinus verse

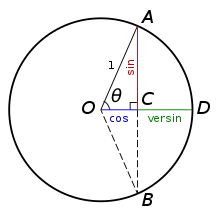
Le sinus verse est une fonction introduite par les Indiens (dans le Surya Siddhanta (c. 400) et dans l'Āryabhaṭīya (VI^e siècle) dérivée de la notion de flèche. Tout comme le sinus indien (jya) c'est une longueur associée à un arc d'un cercle de rayon donné. Appelée utkrama-jya, elle correspond dans un cercle à la flèche de l'arc double, tout comme jya correspond à la demi-corde de l'arc double, c'est-à-dire R sin(θ).

Le terme utkrama signifie « à l'envers », « sortant », « en excès » et explique la traduction en latin (via l'arabe) de utkrama-jya en sinus versus. La table des sinus verse s'obtenait en retranchant au rayon les valeurs des sinus en prenant la table des sinus « à l'envers ». On peut remarquer que, dans une table numérique où sont fournies les différences entre deux sinus consécutifs, les sinus successifs s'obtiennent en additionnant ces différences dans le sens direct, et les sinus verses successifs en les additionnant à partir de la fin[1].

La propriété : ${\displaystyle \sin ^{2}\left({\frac {\theta }{2}}\right)={\frac {1}{2}}{\textrm {versin}}(\theta )}$ a été utilisée par Brahmagupta et Bhaskara pour calculer le sinus de l'angle moitié, pour construire leurs tables de sinus[2].

Les noms et notations pour cette fonction sont très variables. On trouve ainsi : sinus secundus ou sin. sec[3], sinus versus ou s. ver.[4], V.[5], sinver dans les précis de navigation[6], siv.[7].

Historiquement utilisée dans les calculs d'approximation et dans la navigation (par exemple pour le calcul de la distance du grand cercle), elle est tombée en désuétude avec l'arrivée des calculs informatiques.