Snark fleur

En mathématiques, et plus particulièrement en théorie des graphes, les snarks fleurs forment une famille infinie de snarks introduite par Rufus Isaacs en 1975[1].

Snark fleur
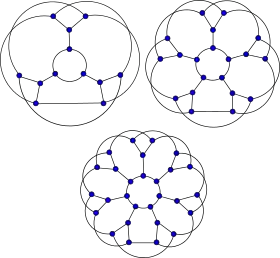Les snarks fleurs J₃, J₅ et J₇

Notation	J_n avec n impair
Nombre de sommets	4n
Nombre d'arêtes	6n
Maille	3 pour n = 3 5 pour n = 5 6 pour n ≥ 7
Nombre chromatique	3
Indice chromatique	4
Propriétés	Snark

Étant un snark, un snark fleur est un graphe cubique connexe et sans isthme d'indice chromatique égal à 4. Il est non-planaire et non-hamiltonien.

Construction

Le snark fleur J_n peut être construit ainsi :

Construire n copies du graphe étoile à 4 sommets. On note le sommet central de chaque étoile A_i et les sommets périphériques B_i, C_i et D_i. On obtient un graphe non connexe à 4n sommets et 3n arêtes.
Construire le cycle à n sommets (B₁ B₂… B_n) (au centre sur les figures). Cela ajoute n arêtes.
Enfin construire le cycle à 2n sommets (C₁C₂… C_nD₁D₂… D_n) (à l'extérieur sur les figures, les arêtes C_nD₁ et D_nC₁ sont en bas). Cela ajoute 2n arêtes.

Par construction, le graphe obtenu J_n est un graphe cubique à 4n sommets et 6n arêtes. Pour être un snark fleur, n doit être impair.

Cas particuliers

Le nom « snark fleur » désigne parfois plus particulièrement J₅, un snark fleur à 20 sommets et 30 arêtes[2]. C'est un des 6 snarks sur 20 sommets suite A130315 de l'OEIS. Le snark fleur J₅ est hypohamiltonien[3].

Le nombre chromatique du graphe fleur J₅ vaut 3.
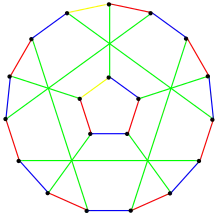L'indice chromatique du graphe fleur J₅ vaut 4.
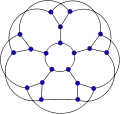La construction du graphe fleur J₅.

J₃ est une variation sur le graphe de Petersen obtenue en appliquant une transformation Y-Δ au graphe de Petersen, en remplaçant un de ses sommets par un triangle. Ce graphe est également connu comme le graphe de Tietze[4]. Pour éviter les cas triviaux, on demande souvent aux snarks d'avoir au moins une maille de 5. Avec cette restriction, J₃ n'est pas un snark.

Le graphe de Tietze J₃

Notes et références

(en) Isaacs, R. « Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable », Amer. Math. Monthly numéro 82, pages 221 à 239, 1975.
(en) Eric W. Weisstein, « Flower Snark », sur MathWorld
(en) Eric W. Weisstein, « Hypohamiltonian Graph », sur MathWorld
(en) L. Clark et R. Entringer, « Smallest maximally nonhamiltonian graphs », Periodica Mathematica Hungarica, vol. 14, n^o 1,‎ 1983, p. 57 à 68 (DOI 10.1007/BF02023582).

Crédits de traduction

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Flower snark » (voir la liste des auteurs).

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Isaacs, R. « Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable », Amer. Math. Monthly numéro 82, pages 221 à 239, 1975.

[2] (en) Eric W. Weisstein, « Flower Snark », sur MathWorld

[3] (en) Eric W. Weisstein, « Hypohamiltonian Graph », sur MathWorld

[4] (en) L. Clark et R. Entringer, « Smallest maximally nonhamiltonian graphs », Periodica Mathematica Hungarica, vol. 14, n^o 1,‎ 1983, p. 57 à 68 (DOI 10.1007/BF02023582).