Spline cubique d'Hermite

Chaque polynôme ${\displaystyle P_{i}(x)}$ se trouve sous la forme suivante :

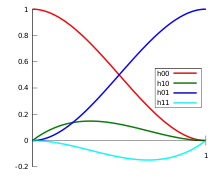
Les quatre polynômes de base

${\displaystyle P_{i}\in Vect\{h_{00},h_{10},h_{01},h_{11}\}\,}$

avec

${\displaystyle h_{00}(t)=2t^{3}-3t^{2}+1\,\!}$

${\displaystyle h_{10}(t)=t^{3}-2t^{2}+t\,\!}$

${\displaystyle h_{01}(t)=-2t^{3}+3t^{2}\,\!}$

${\displaystyle h_{11}(t)=t^{3}-t^{2}\,\!}$

ce qui donne le polynôme suivant :

${\displaystyle p(t)=h_{00}(t)p_{0}+h_{10}(t)m_{0}+h_{01}(t)p_{1}+h_{11}(t)m_{1}.}$

Sous cette écriture, il est possible de voir que le polynôme p vérifie :

${\displaystyle p(0)=p_{0},\,p(1)=p_{1},\,p'(0)=m_{0}{\text{ et }}p'(1)=m_{1}.}$

La courbe est déterminée par la position des points et des tangentes.

Pour trouver le polynôme tel que : ${\displaystyle P(x_{0})=p_{0},\;P(x_{1})=p_{1},\;P'(x_{0})=m_{0},\;P'(x_{1})=m_{1}}$ il faut poser :

${\displaystyle p(t)=h_{00}(t)p_{0}+h_{10}(t)m_{0}\cdot (x_{1}-x_{0})+h_{01}(t)p_{1}+h_{11}(t)m_{1}\cdot (x_{1}-x_{0}).\!}$

et

${\displaystyle P(x)=p\left({\frac {x-x_{0}}{x_{1}-x_{0}}}\right)}$

alors :

${\displaystyle P(x_{0})=p\left({\frac {x_{0}-x_{0}}{x_{1}-x_{0}}}\right)=p(0)=p_{0},\ P(x_{1})=p\left({\frac {x_{1}-x_{0}}{x_{1}-x_{0}}}\right)=p(1)=p_{1}}$

${\displaystyle P'(x)={\frac {1}{x_{1}-x_{0}}}p'\left({\frac {x-x_{0}}{x_{1}-x_{0}}}\right)}$

d'où

${\displaystyle P'(x_{0})={\frac {1}{x_{1}-x_{0}}}p'\left({\frac {x_{0}-x_{0}}{x_{1}-x_{0}}}\right)={\frac {1}{x_{1}-x_{0}}}p'(0)=m_{0}(x_{1}-x_{0})\cdot {\frac {1}{x_{1}-x_{0}}}=m_{0},}$

${\displaystyle P'(x_{1})={\frac {1}{x_{1}-x_{0}}}p'\left({\frac {x_{1}-x_{0}}{x_{1}-x_{0}}}\right)={\frac {1}{x_{1}-x_{0}}}p'(1)=m_{1}(x_{1}-x_{0})\cdot {\frac {1}{x_{1}-x_{0}}}=m_{1}.}$