Surface idéale

Une surface solide idéale est plate, rigide, parfaitement lisse et chimiquement homogène, et a une hystérésis d'angle de contact nulle. L'hystérésis nulle implique que les angles de contact d'avance et de recul sont égaux. En d'autres termes, il existe un seul angle de contact thermodynamiquement stable. Lorsqu'une goutte de liquide est placée sur une telle surface, l'angle de contact caractéristique est formé comme illustré à la Fig. 1.

Figure 1 : Angle de contact d'une goutte de liquide sur une surface solide

Figure 2 : « Mouillage » de différents fluides : A montre un fluide avec très peu de mouillage, tandis que C montre un fluide avec plus de mouillage. A a un grand angle de contact et C a un petit angle de contact.

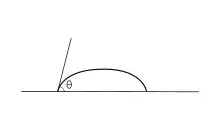
De plus, sur une surface idéale, la goutte reprend sa forme originelle si elle est perturbée[1]. Les dérivations suivantes s'appliquent uniquement aux surfaces solides idéales ; ils ne sont valables que pour l'état dans lequel les interfaces ne bougent pas et la ligne limite de phase existe en équilibre.

Minimisation de l'énergie: trois phases

Figure 3 : Coexistence de trois phases fluides en contact mutuel : α, β et θ représentent à la fois les étiquettes des phases et les angles de contact.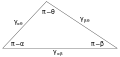
Figure 4 : Triangle de Neumann reliant les énergies de surface et les angles de contact de trois phases fluides coexistant en équilibre statique, comme le montre la figure 3.

La figure 3 montre la ligne de contact où trois phases se rencontrent. À l'équilibre, la force nette – par unité de longueur, le long de la ligne de démarcation entre les trois phases – doit être nulle. Les composantes de la force nette dans la direction le long de chacune des interfaces sont données par :

\gamma _{\alpha \theta }+\gamma _{\theta \beta }\cos {\theta }+\gamma _{\alpha \beta }\cos {\alpha }\ =0

\gamma _{\alpha \theta }\cos {\theta }+\gamma _{\theta \beta }+\gamma _{\alpha \beta }\cos {\beta }\ =0

\gamma _{\alpha \theta }\cos {\alpha }+\gamma _{\theta \beta }\cos {\beta }+\gamma _{\alpha \beta }\ =0

où α, β et θ sont les angles indiqués (fig.4) et γ _ij est l'énergie de surface entre les deux phases indiquées.

Ces relations peuvent également être exprimées par un analogue à un triangle connu sous le nom de triangle de Neumann (illustré à la figure 4). Le triangle de Neumann est compatible avec la restriction géométrique $\alpha +\beta +\theta =2\pi$ ; en lui appliquant la loi des sinus et la loi des cosinus on produit des relations qui décrivent comment les angles interfaciaux dépendent des rapports des énergies de surface[2].

Parce que ces trois énergies de surface forment les côtés d'un triangle, elles sont contraintes par les inégalités du triangle, γ _ij < γ _jk + γ _ik signifiant qu'aucune des tensions de surface ne peut dépasser la somme des deux autres. Si trois fluides avec des énergies de surface qui ne suivent pas ces inégalités sont mis en contact, aucune configuration d'équilibre compatible avec la figure 3 n'existera.

Simplification vers une géométrie plane, relation de Young

Si la phase β est remplacée par une surface rigide plane, comme le montre la figure 5, alors β = π, et la deuxième équation de force nette se simplifie en équation de Young[3]:

Figure 5 : Angle de contact d'une gouttelette de liquide mouillée sur une surface solide rigide

\gamma _{SG}\ =\gamma _{SL}+\gamma _{LG}\cos {\theta }

[4]

qui relie les tensions superficielles entre les trois phases : solide, liquide et gazeuse . Par la suite, cela prédit l'angle de contact d'une goutte de liquide sur une surface solide à partir de la connaissance des trois énergies de surface impliquées. Cette équation s'applique également si la phase « gazeuse » est celle d'un autre liquide, non miscible avec la gouttelette de la première phase « liquide ».

Vraies surfaces lisses et angle de contact de Young

L'équation de Young suppose une surface parfaitement plane et rigide. Dans la plupart des cas, les surfaces sont loin de cette situation « idéale », et deux sont considérées ici : le cas des surfaces rugueuses et le cas des surfaces lisses encore réelles (finies et rigides).

Même dans une surface parfaitement lisse, une goutte prendra un large éventail d'angles de contact allant de l'angle de contact dit d'avancement, $\theta _{\mathrm {A} }$ , à l'angle de contact dit de recul, $\theta _{\mathrm {R} }$ . L'angle de contact d'équilibre ( $\theta _{\mathrm {c} }$ ) peut être calculé à partir de $\theta _{\mathrm {A} }$ et $\theta _{\mathrm {R} }$ comme l'a montré Tadmor[5] de sorte que:

\theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos {\theta _{\mathrm {A} }}+r_{\mathrm {R} }\cos {\theta _{\mathrm {R} }}}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)

où

r_{\mathrm {A} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {A} }}}{2-3\cos {\theta _{\mathrm {A} }}+\cos ^{3}{\theta _{\mathrm {A} }}}}\right)^{1/3}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {R} }}}{2-3\cos {\theta _{\mathrm {R} }}+\cos ^{3}{\theta _{\mathrm {R} }}}}\right)^{1/3}

Équation de Young-Dupré et coefficient d'étalement

L'équation de Young-Dupré (Thomas Young 1805, Lewis Dupré 1855) stipule que ni γ _SG ni γ _SL ne peuvent être supérieurs à la somme des deux autres énergies de surface. La conséquence de cette restriction est la prédiction d'un mouillage complet lorsque γ _SG > γ _SL + γ _LG et d'un mouillage nul lorsque γ _SL > γ _SG + γ _LG . L'absence de solution à l'équation de Young-Dupré est un indicateur qu'il n'y a pas de configuration d'équilibre avec un angle de contact entre 0 et 180° pour ces situations.

Un paramètre utile pour jauger le mouillage est le paramètre d'étalement S ,

S\ =\gamma _{SG}-(\gamma _{SL}+\gamma _{LG})

Lorsque S > 0, le liquide mouille complètement la surface (mouillage complet). Lorsque S < 0, un mouillage partiel se produit.

La combinaison de la définition du paramètre d'étalement avec la relation de Young donne l'équation de Young – Dupré :

S\ =\gamma _{LG}(\cos \theta -1)

qui n'a de solutions physiques pour θ que lorsque S < 0.

Voir également

Références

Johnson, Rulon E. (1993) in Wettability Ed. Berg, John. C. New York, NY: Marcel Dekker, Inc. (ISBN 0-8247-9046-4)
J.S. Rowlinson et Widom, B., Molecular Theory of Capillarity, Oxford, UK, Clarendon Press, 1982 (ISBN 0-19-855642-X)
Young, « An Essay on the Cohesion of Fluids », Phil. Trans. R. Soc. Lond., vol. 95,‎ 1805, p. 65–87 (DOI 10.1098/rstl.1805.0005)
T. S. Chow, « Wetting of rough surfaces », Journal of Physics: Condensed Matter, vol. 10, n^o 27,‎ 1998, p. L445 (DOI 10.1088/0953-8984/10/27/001, Bibcode 1998JPCM...10L.445C)
Tadmor, « Line energy and the relation between advancing, receding and Young contact angles », Langmuir, vol. 20, n^o 18,‎ 2004, p. 7659–64 (PMID 15323516, DOI 10.1021/la049410h)

Liens externes

Effet de la rugosité de surface sur l'angle de contact

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[Johnson-1] Johnson, Rulon E. (1993) in Wettability Ed. Berg, John. C. New York, NY: Marcel Dekker, Inc. (ISBN 0-8247-9046-4)

[2] J.S. Rowlinson et Widom, B., Molecular Theory of Capillarity, Oxford, UK, Clarendon Press, 1982 (ISBN 0-19-855642-X)

[3] Young, « An Essay on the Cohesion of Fluids », Phil. Trans. R. Soc. Lond., vol. 95,‎ 1805, p. 65–87 (DOI 10.1098/rstl.1805.0005)

[4] T. S. Chow, « Wetting of rough surfaces », Journal of Physics: Condensed Matter, vol. 10, n^o 27,‎ 1998, p. L445 (DOI 10.1088/0953-8984/10/27/001, Bibcode 1998JPCM...10L.445C)

[Tadm-5] Tadmor, « Line energy and the relation between advancing, receding and Young contact angles », Langmuir, vol. 20, n^o 18,‎ 2004, p. 7659–64 (PMID 15323516, DOI 10.1021/la049410h)