Théorème d'Erdős-Szekeres

En mathématiques, et notamment en géométrie discrète, le théorème d'Erdős-Szekeres est une version finitaire d'un corollaire du théorème de Ramsey. Alors que le théorème de Ramsey permet de prouver facilement que toute suite infinie de réels distincts contient au moins une sous-suite infinie croissante ou une sous-suite infinie décroissante, le résultat prouvé par Paul Erdős et George Szekeres est plus précis en donnant des bornes sur les longueurs des suites. L'énoncé est le suivant :

Soient r et s deux entiers. Toute suite d'au moins (r – 1)(s – 1) + 1 nombres réels contient une sous-suite croissante de longueur r ou une sous-suite décroissante de longueur s.

Dans le même article de 1935 où ce résultat est démontré figure aussi le Happy Ending problem[1].

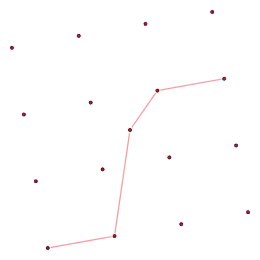
Un chemin de quatre segments de pente positive dans un ensemble de 17 points. On considère la suite des ordonnées des 17 points triés par abscisses croissantes ; le théorème d'Erdős-Szekeres assure alors qu'il quatre segments consécutifs de pente positive ou quatre segments consécutifs de pente négative. Si le point central est omis, un tel chemin n'existe pas.

Un exemple

Pour r = 3 et s = 2, l'énoncé dit que toute permutation de trois nombres contient une sous-suite croissante de longueur 3 ou une sous-suite décroissante de longueur 2. Parmi les six permutations de {1, 2, 3} :

(1, 2, 3) est une suite croissante ;
(1, 3, 2) contient la sous-suite décroissante (3, 2) ;
(2, 1, 3) et (2, 3, 1) contiennent la sous-suite décroissante (2, 1) ;
(3, 1, 2) et (3, 2, 1) contiennent les sous-suites décroissantes (3, 1) et (3, 2).

Interprétation géométrique

Étant donné un ensemble de points dans le plan euclidien, on forme une suite en triant les points par abscisses croissantes ; les nombres comparés dans le théorème d'Erdős-Szekeres sont alors les ordonnées des points. Dans ce contexte, le théorème affirme que s'il y a au moins rs + 1 points, on peut trouver une ligne polygonale de r segments de pentes positives, ou de s segments de pentes négatives. Par exemple, en prenant r = s = 4, tout ensemble de 17 points contient une ligne polygonale composée de quatre segments qui ont tous une pente de même signe.

Un exemple qui montre que la borne est atteinte, c'est-à-dire que rs points ne suffisent pas pour obtenir une telle ligne polygonale, consiste à prendre une grille régulière de rs points et de lui appliquer une légère rotation.

Démonstrations

Le théorème d'Erdős-Szekeres peut être prouvé de diverses manières ; Steele passe en revue six preuves différentes, parmi lesquelles les deux suivantes[2]. D'autres preuves décrites par Steele incluent la preuve originale d'Erdős et Szekeres, celles de Blackwell[3], Hammersley[4] et Lovász[5].

Principe des tiroirs

Étant donné une suite de (r – 1)(s – 1) + 1 points, on étiquette le i-ème nombre n_i de la suite par un couple (a_i, b_i) d'entiers positifs, où a_i est la longueur de la plus longue sous-suite croissante qui se termine par n_i, et b_i est la longueur de la plus longue sous-suite décroissante qui se termine par n_i. Deux nombres de la suite sont étiquetés par des paires distinctes : en effet, soient i < j deux indices ; si n_i < n_j, alors a_i < a_j ; si au contraire n_i > n_j, alors b_i < b_j. D'autre part, il n'y a que (r – 1)(s – 1) couples tels que a_i < r et b_i < s. Par le principe des tiroirs, il existe un entier i tel que a_i ≥ r ou b_i ≥ s ; dans le premier cas, n_i fait partie d'une sous-suite croissante de longueur au moins r et dans le deuxième cas, n_i fait partie d'une sous-suite décroissante de longueur au moins s.

Steele attribue cette preuve à Seidenberg (en)[6] et l'appelle, dans son article de synthèse[2], la « preuve la plus lisse et la plus systématique ».

Théorème de Dilworth

Un autre preuve fait appel au théorème de Dilworth sur la décomposition en chaînes d'un ordre partiel, ou à sa version duale, le théorème de Mirsky (en).

Pour cela, on définit un ordre partiel sur les nombres de la suite par : x est inférieur ou égal à y dans cet ordre partiel si x ≤ y comme nombres, et si x figure avant y dans la suite. Une chaîne dans cet ordre est une sous-suite croissante, et une antichaîne est une sous-suite décroissante. Par le théorème de Mirsky (en), s'il n'existe pas de chaîne de longueur r, la suite peut être partitionnée en au plus r – 1 antichaînes ; la plus longue de ces antichaînes forme alors un sous-suite décroissante de longueur au moins

\left\lceil {\frac {(r-1)(s-1)+1}{r-1}}\right\rceil =s.

De manière duale, par le théorème de Dilworth lui-même, s'il n'existe pas d'antichaîne de longueur s, alors la suite peut être partitionnée en au plus s – 1 chaînes, et la plus longue doit avoir longueur au moins r.

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Erdős–Szekeres theorem » (voir la liste des auteurs).

(en) Paul Erdős et George Szekeres, « A combinatorial problem in geometry », Compos. Math., vol. 2,‎ 1935, p. 463-470 (lire en ligne).
(en) J. Michael Steele, « Variations on the monotone subsequence theme of Erdős and Szekeres », dans David Aldous, Persi Diaconis, Joel Spencer et J. Michael Steele (éditeurs), Discrete Probability and Algorithms, Springer-Verlag, coll. « IMA Volumes in Mathematics and its Applications » (n^o 72), 1995 (lire en ligne), p. 111-131.
(en) Paul Blackwell, « An alternative proof of a theorem of Erdős and Szekeres », Amer.Math. Monthly, vol. 78, n^o 3,‎ 1971, p. 273 (JSTOR 2317525).
(en) John M. Hammersley, « A few seedlings of research », dans Proc. 6th Berkeley Symp. Math. Stat. Prob., University of California Press, 1972, p. 345-394.
(en) László Lovász, Combinatorial Problems and Exercises, North-Holland, 1979, Solution to Exercise 14.25.
(en) Abraham Seidenberg, « A simple proof of a theorem of Erdős and Szekeres », J. London Math. Soc., vol. 34,‎ 1959, p. 352 (lire en ligne).

Voir aussi

Article connexe

Problème de la plus longue sous-suite croissante (en)

Lien externe

(en) Eric W. Weisstein, « Erdős-Szekeres Theorem », sur MathWorld

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Paul Erdős et George Szekeres, « A combinatorial problem in geometry », Compos. Math., vol. 2,‎ 1935, p. 463-470 (lire en ligne).

[steele-2] (en) J. Michael Steele, « Variations on the monotone subsequence theme of Erdős and Szekeres », dans David Aldous, Persi Diaconis, Joel Spencer et J. Michael Steele (éditeurs), Discrete Probability and Algorithms, Springer-Verlag, coll. « IMA Volumes in Mathematics and its Applications » (n^o 72), 1995 (lire en ligne), p. 111-131.

[Blackwell-3] (en) Paul Blackwell, « An alternative proof of a theorem of Erdős and Szekeres », Amer.Math. Monthly, vol. 78, n^o 3,‎ 1971, p. 273 (JSTOR 2317525).

[Hammersley-4] (en) John M. Hammersley, « A few seedlings of research », dans Proc. 6th Berkeley Symp. Math. Stat. Prob., University of California Press, 1972, p. 345-394.

[Lovász-5] (en) László Lovász, Combinatorial Problems and Exercises, North-Holland, 1979, Solution to Exercise 14.25.

[Seidenberg-6] (en) Abraham Seidenberg, « A simple proof of a theorem of Erdős and Szekeres », J. London Math. Soc., vol. 34,‎ 1959, p. 352 (lire en ligne).