Théorème de Clairaut (géométrie)

Le théorème de Clairaut en géométrie est une généralisation du théorème de Pythagore, où les égalités d'aires entre carrés construits sur les côtés d'un triangle rectangle, deviennent des égalités d'aire entre parallélogrammes construits sur les côtés d'un triangle quelconque. En français, il porte souvent le nom d'un frère du mathématicien Alexis Claude Clairaut, bien qu'il soit dû en réalité à Pappus d'Alexandrie (IVe siècle apr. J.-C.)[1].

Théorème de Clairaut

Pour les articles homonymes, voir Théorèmes de Clairaut.

Énoncé
  • Si ABC est un triangle
  • Si ABDE et ACFG sont des parallélogrammes extérieurs au triangle
  • Si (DE) et (FG) se coupent en O
  • Si, enfin, BCHI est un parallélogramme extérieur au triangle tel que [OA] et [CH] soient parallèles de même longueur

alors

  • L'aire du parallélogramme BCHI est égale à la somme des aires des deux autres parallélogrammes
Preuve

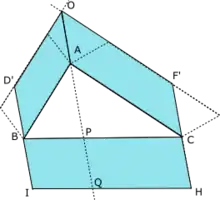
Démonstration

Il suffit de déformer les parallélogrammes sans modifier leur aire.

Puisque OF'CA, CHIB, BD'OA sont des parallélogrammes, "[OA] et [CH] soient parallèles de même longueur" implique que [BD'], [IB], [QP], [HC] et [CF'] y sont également parallèles de même longueur.

aire(ABDE) =aire(ABD'O) (même base, même hauteur)
aire(ACFG) = aire(ACF'O)

Si la droite OA rencontre (BC) et (HI) en P et Q alors

aire(ABD'O) =aire(BIQP) (même base, même hauteur)
aire(ACF'O) = aire(CHQP)
Clairaut et Pythagore

Cas particulier

Si ABC est un triangle rectangle en A, si ABDE et ACFG sont des carrés, on montre que la droite OA est perpendiculaire à l'hypoténuse BC du triangle et de même longueur, et alors BCHI est aussi un carré. On retrouve alors l'égalité du théorème de Pythagore.

Histoire

Le théorème apparaît à la proposition 1 du livre IV de la Collection mathématique de Pappus[2]. Le parallélogramme est construit sur l'hypoténuse du même côté que le triangle (ce qui permet une construction géométrique simple de celui-ci).

En France le théorème porte souvent le nom de Clairaut, mais il s'agit, non pas du mathématicien du XVIIIe siècle bien connu Alexis Claude Clairaut, mais de son frère cadet, mathématicien précoce mort prématurément, et auteur de deux publications en géométrie élémentaire[1],[3]. Le nom de Clairaut reste attaché au théorème, bien que dès 1778 Jean-Étienne Montucla l'attribuait déjà à Pappus dans une réédition des Récréations mathématiques et physiques de Jacques Ozanam[1],[4].

Références
  1. F.G.-M. (Frère Gabriel-Marie), Exercices de géométrie, Tours, A. Mame et fils, , 5e éd. (lire en ligne), p. 740-741, §1559 a.
  2. Bernard Vitrac, Euclide Les Éléments Volume 1. Introduction générale(Maurice Caveing). Livres I à IV, PUF, , notices du livre I, p 285-286, Vitrac ne mentionne pas Clairaut.
  3. F.G-M. cite J. Aicard, Desportes, Paul Gervais... [et al.], Un million de faits, , 10e éd. (lire en ligne), p. 131, voir aussi la première édition (1842) même page.
  4. Jacques Ozanam et Jean-Etienne Montucla, Récréations mathématiques et physiques, volume 1, Paris, C.-A. Jombert, (lire en ligne) p. 290-291, planche 4 fig. 30, et pour l'attribution à Pappus p. 454-455. Il est bien question de « Clairaut le jeune » p. 454, mais à propos d'un autre théorème qui est aussi une généralisation de Pythagore, théorème connu aujourd'hui comme théorème de Thabit ibn Qurra, voir à ce propos (en) Carl B. Boyer, « Clairaut le cadet and a Theorem of Thâbit ibn Qurra », Isis, vol. 55,‎ , p. 68-70 (lire en ligne). Le théorème de Thâbit ibn Qurra a bien été publié par le frère cadet de Clairaut : « Proposition élémentaire de géométrie », Journal des sçavans,‎ , p. 273-274 (lire en ligne), voir Olivier Courcelle, « 14 août 1729 (1) : Clairaut le cadet est à la Société des arts », .
  • Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.