Théorème de Newton (transversale)

En géométrie algébrique, le théorème de Newton précise une invariance sur les rapports de produits des longueurs dessinées par des droites coupant une courbe algébrique.

Illustration du théorème de Newton : pour cette courbe algébrique plane et ces couples de droites parallèles, on a

{\frac {MA\cdot MB}{MC\cdot MD}}={\frac {NE\cdot NF}{NG\cdot NH}}

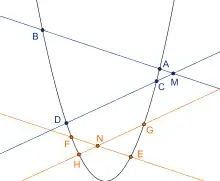
Plus précisément, on considère une courbe plane Γ algébrique de degré n et ${\vec {d_{1}}}$ et ${\vec {d_{2}}}$ deux directions de droites.

Pour tout point M, si la droite $(M,{\vec {d_{1}}})$ (resp. la droite $(M,{\vec {d_{2}}})$ ) rencontre la courbe en n points $A_{1,M},A_{2,M}\dots ,A_{n,M}$ (resp. $B_{1,M},B_{2,M}...,B_{n,M}$ alors le rapport ${\frac {MA_{1,M}\cdot MA_{2,M}\cdots MA_{n,M}}{MB_{1,M}\cdot MB_{2,M}\cdots MB_{n,M}}}$ est indépendant du point M.

Principe de démonstration

Le principe de la démonstration s'appuie sur le fait que, dans un polynôme de degré n, le produit des racines est égal à $(-1)^{n}{\frac {c_{0}}{c_{n}}}$ .

La courbe algébrique a pour équation F(x,y) = 0.

On note ${\vec {u_{1}}}=(\cos \theta _{1},\sin \theta _{1})$ (resp. ${\vec {u_{2}}}=(\cos \theta _{2},sin\theta _{2})$ un vecteur unitaire de même direction que ${\vec {d_{1}}}$ (resp. ${\vec {d_{2}}}$ ).

Si M a pour coordonnées (a, b), les mesures algébriques ${\overline {MA_{i,M}}}$ sont les racines du polynôme en λ, $F(a+\lambda \cos \theta _{1},b+\lambda \sin \theta _{1})$ . Dans ce polynôme, le coefficient constant est F(a,b) et le coefficient du terme de degré n ne dépend que du polynôme F et de l'angle θ₁. En particulier, ce coefficient $c_{F,\theta _{1}}$ ne dépend pas des valeurs a et b.

On a alors

MA_{1,M}\cdot MA_{2,M}\cdots MA_{n,M}=\left|{\frac {F(a,b)}{c_{F,\theta _{1}}}}\right|

MB_{1,M}\cdot MB_{2,M}\cdots MB_{n,M}=\left|{\frac {F(a,b)}{c_{F,\theta _{2}}}}\right|

{\frac {MA_{1,M}\cdot MA_{2,M}\cdots MA_{n,M}}{MB_{1,M}\cdot MB_{2,M}\cdots MB_{n,M}}}=\left|{\frac {c_{F,\theta _{2}}}{c_{F,\theta _{1}}}}\right|

Ce rapport est bien indépendant de M.

Applications

Si la courbe est un cercle, on retrouve la puissance d'un point par rapport à un cercle car on a

{\frac {{\overline {MA_{1}}}\cdot {\overline {MA_{2}}}}{{\overline {MB_{1}}}\cdot {\overline {MB_{2}}}}}={\frac {{\overline {\Omega C_{1}}}\cdot {\overline {\Omega C_{2}}}}{{\overline {\Omega D_{1}}}\cdot {\overline {\Omega D_{2}}}}}={\frac {-r^{2}}{-r^{2}}}=1

ce qui prouve l'invariance du produit des mesures algébriques quand on change la direction de la droite.

De plus, la démonstration fournit la valeur de cette puissance. Pour un cercle d'équation $x^{2}+y^{2}-2\alpha x-2\beta y+c=0$ (où α et β sont les coordonnées du centre), on a ${c_{F,\theta }}=1$ et donc

{\overline {MA_{1}}}\cdot {\overline {MA_{2}}}=F(a,b)

où a et b sont les coordonnées du point M.

Ce théorème intervient aussi dans la démonstration du théorème de Maclaurin sur les transversales et les tangentes[1]

Bibliographie

Charles-Emilie Page, Complément de géométrie analytique, 1841, pp. 83-84

Notes et références

Terquem, «Théorème de Mac-Laurin sur les courbes algébriques planes et conséquences géométriques du théorème analytique de M. Jacobi», Nouvelles annales de mathématiques, 1^re série, tome 9 (1950), pp 440-451

Portail des mathématiques
Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Terquem, «Théorème de Mac-Laurin sur les courbes algébriques planes et conséquences géométriques du théorème analytique de M. Jacobi», Nouvelles annales de mathématiques, 1^re série, tome 9 (1950), pp 440-451