Théorème de l'étoile de David

Le théorème de l'étoile de David est un résultat mathématique donnant deux identités concernant les coefficients binomiaux, disposés dans le triangle de Pascal en forme de deux triangles imbriqués.

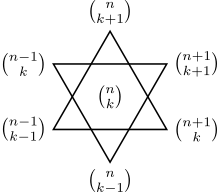
Coefficients binomiaux intervenant dans le théorème de l'étoile de David (les lignes du triangle de Pascal sont représentées ici verticalement).

Première identité

Énoncé

Les PGCD des coefficients binomiaux situés aux sommets de deux triangles d'une étoile de David dans le triangle de Pascal sont égaux :

{\begin{aligned}&{\text{PGCD}}{\biggl (}{\binom {n-1}{k-1}},{\binom {n}{k+1}},{\binom {n+1}{k}}{\biggr )}\\[8pt]={}&{\text{PGCD}}{\biggl (}{\binom {n-1}{k}},{\binom {n}{k-1}},{\binom {n+1}{k+1}}{\biggr )}\end{aligned}}

Historique

Cette identité a été conjecturée par Henry W. Gould en 1971[1], démontrée par Hoggatt et Hillman en 1972[2], puis par Singmaster en 1973[3], et par Hitotumatu et Sato en 1975[4].

Exemples

Pour n = 9, k = 3 ou n = 9, k = 6, le nombre 84 est entouré successivement par les nombres 28, 56, 126, 210, 120, 36. En prenant un terme sur deux, on obtient : PGCD (28, 126, 120) = 2 = PGCD (56, 210, 36) (voir ci-contre).

De même, le terme précédent 36 est entouré par les éléments 8, 28, 84, 120, 45, 9, et en prenant un terme sur deux, on obtient : PGCD (8, 84, 45)= 1 = PGCD (28, 120, 9).

Démonstration de Hitotumatu et Sato

La formule :

${\begin{bmatrix}{\binom {n-1}{k-1}}\\{\binom {n}{k+1}}\\{\binom {n+1}{k}}\end{bmatrix}}={\begin{bmatrix}k+1&k-n-1&-n-1\\-k&n-k+1&n\\k+1&k-n&-n\end{bmatrix}}{\begin{bmatrix}{\binom {n+1}{k+1}}\\{\binom {n}{k-1}}\\{\binom {n-1}{k}}\end{bmatrix}}$

et la formule inverse :

${\begin{bmatrix}{\binom {n+1}{k+1}}\\{\binom {n}{k-1}}\\{\binom {n-1}{k}}\end{bmatrix}}={\begin{bmatrix}-n&-k&n-k+1\\n&k+1&k-n\\-n-1&-k-1&n-k+1\end{bmatrix}}{\begin{bmatrix}{\binom {n-1}{k-1}}\\{\binom {n}{k+1}}\\{\binom {n+1}{k}}\end{bmatrix}}$

montrent que chaque élément d'un triangle est combinaison linéaire entière des éléments de l'autre triangle, ce qui implique que les diviseurs communs aux élément d'un triangle, sont des diviseurs communs aux éléments de l'autre triangle et vice versa. Ceci prouve l'égalité des PGCD.

Généralisations

Singmaster [3] a complété cette identité en montrant que les PGCD ci-dessus sont également égaux à ${\text{PGCD}}{\biggl (}{n-1 \choose k-2},{n-1 \choose k-1},{n-1 \choose k},{n-1 \choose k+1}{\biggr )}$ .

Ainsi, dans l'exemple ci-dessus pour l'élément 84, on a également PGCD {8, 28, 56, 70} = 2.

Ces égalités persistent aussi pour des étoiles plus grandes[5]. Par exemple,

{\begin{aligned}&{\text{PGCD}}{\biggl (}{\binom {n-2}{k-2}},{\binom {n-1}{k}},{\binom {n}{k+2}},{\binom {n+1}{k+1}},{\binom {n+2}{k}},{\binom {n}{k-1}}{\biggr )}\\[8pt]={}&{\text{PGCD}}{\biggl (}{\binom {n-2}{k}},{\binom {n-1}{k-1}},{\binom {n}{k-2}},{\binom {n+1}{k}},{\binom {n+2}{k+2}},{\binom {n}{k+1}}{\biggr )}.\end{aligned}}

Deuxième identité

Énoncé

Hoggatt et Hansell ont remarqué en 1971 que les deux ensembles de trois nombres de l'étoile de David ont des produits égaux [6] :

{\binom {n-1}{k-1}}{\binom {n}{k+1}}{\binom {n+1}{k}}={\binom {n-1}{k}}{\binom {n}{k-1}}{\binom {n+1}{k+1}}

.

Par exemple, en observant à nouveau que l'élément 84 est entouré successivement par les éléments 28, 56, 126, 210, 120, 36, et en prenant un terme sur deux, on a : 28 × 126 × 120 = 2⁶ × 3³ × 5 × 7² = 56 × 210 × 36.

Ce résultat se démontre facilement en écrivant chaque coefficient binomial sous forme factorielle : ${n \choose k}={\frac {n!}{(n-k)!k!}}$ .

Il en existe cependant une démonstration combinatoire, moins simple :

Démonstration

Soient $a, b, c, x, y, z$ six entiers naturels vérifiant $x, y, z \leq min(a, b, c)$ et $(b-a, c-b, a-c) = (y-z, z-x, x-y)$ .

Comptons le nombre de façons de partitionner un ensemble de taille $a + b + c$ en six parties :

$A$ , de taille $x$ , $B$ , de taille $y$ , $C$ , de taille $z$
$A'$ , de taille $a - x$ , $B'$ , de taille $b - y$ , $C'$ , de taille $c - z$ .

On commence par partitionner l'ensemble en trois parties, de tailles respectives $a$ , $b$ et $c$ . Il y a un certain nombre $N$ de façons de le faire.

Méthode 1

on coupe la partie de taille $a$ en $A\sqcup A'$ : ${\binom {a}{x}}$ façons.
on coupe la partie de taille $b$ en $B\sqcup B'$ : ${\binom {b}{y}}$ façons.
on coupe la partie de taille $c$ en $C\sqcup C'$ : ${\binom {c}{z}}$ façons.

Total : $N\times {\binom {a}{x}}{\binom {b}{y}}{\binom {c}{z}}$ façons.

Méthode 2

on coupe la partie de taille $a$ en $C\sqcup B'$ (car $z+b-y=a$ ) : ${\binom {a}{z}}$ façons.
on coupe la partie de taille $b$ en $A\sqcup C'$ (car $x+c-z=b$ ) : ${\binom {b}{x}}$ façons.
on coupe la partie de taille $c$ en $B\sqcup A'$ (car $y+a-x=c$ ) : ${\binom {c}{y}}$ façons

Total : $N\times {\binom {a}{z}}{\binom {b}{x}}{\binom {y}{z}}$ façons.

On obtient ${\binom {a}{x}}{\binom {b}{y}}{\binom {c}{z}}={\binom {a}{z}}{\binom {b}{x}}{\binom {c}{y}}$ .

Posant maintenant $(a, b, c) = (n -1, n, n +1)$ et $(x, y, z) = (k -1, k +1, k)$ , on vérifie que $(b-a, c-b, a-c) = (1, 1, -2) = (y-z, z-x, x-y)$ .

On en déduit l'identité de l'étoile de David : ${\binom {n-1}{k-1}}{\binom {n}{k+1}}{\binom {n+1}{k}}={\binom {n-1}{k}}{\binom {n}{k-1}}{\binom {n+1}{k+1}}$ .

Cette démonstration est une traduction/adaptation de celle publiée sur ce site.

Généralisation

On peut remplacer ${n \choose k}$ par ${\binom {n}{k}}_{(a_{n})}={\frac {f(n)}{f(n-k)f(k)}}$ , où $f(n)=\coprod _{k=1}^{n}a_{k}$ , $(a_{n})$ étant une suite de réels non nuls.

En particulier, si $(a_{n})$ est la suite de Fibonacci $(F_{n})$ , ${\binom {n}{k}}_{(a_{n})}$ est le coefficient fibonomial ${\binom {n}{k}}_{F}$ ; le deuxième théorème de l'étoile de David est donc valable dans le triangle fibonomial.[5]

Si $(a_{n})$ est le q-analogue de n : $[n]_{q}=1+q+...+q^{n-1}$ , ${\binom {n}{k}}_{(a_{n})}$ est le coefficient binomial de Gauss ${\binom {n}{k}}_{q}$ ; le deuxième théorème de l'étoile de David est donc valable dans le triangle q-binomial.

On peut généraliser au cas où $(a_{n})$ est une suite quelconque dans un groupe commutatif noté multiplicativement. Par exemple, dans le groupe $(\mathbb {Z} ,+)$ , ${\binom {n}{k}}_{(n)}=k(n-k)$ , voir la suite A004247 de l'OEIS.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Star of David theorem » (voir la liste des auteurs).

(en) HW Gould,, « A New Greatest Common Divisor Property of The Binomial Coefficients », Fibonacci Quarterly 10,‎ 1972, p. 579 – 584 (lire en ligne)
(en) Hillman, A.P. and Hoggatt, Jr., V.E., « “A Proof of Gould's Pascal Hexagon Conjecture.” », The Fibonacci Quarterly, Vol. 10.6,‎ 1972, p. 565–568, 598 (lire en ligne)
(en) David Singmaster, « "Notes on Binomial Coefficients: IV—Proof of a Conjecture of Gould on the G.C.D.'s of Two Triples of Binomial Coefficients." », The Fibonacci Quarterly 11.3,‎ 1973, p. 282-84
(en) Sin Hitotumatu et Daihachiro Sato, « Star of David theorem », Fibonacci Quarterly 13,‎ 1975, p. 70
Weisstein, Eric W. "Star of David Theorem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/StarofDavidTheorem.html
(en) V. E. HOGGATT et W. HANSELL, « THE HIDDEN HEXAGON SQUARES », Fibonacci quarterly vol. 9 n°2,‎ 1971, p. 120,133 (lire en ligne)

Lien externe

Visualisation du second théorème de l'étoile de David.

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) HW Gould,, « A New Greatest Common Divisor Property of The Binomial Coefficients », Fibonacci Quarterly 10,‎ 1972, p. 579 – 584 (lire en ligne)

[2] (en) Hillman, A.P. and Hoggatt, Jr., V.E., « “A Proof of Gould's Pascal Hexagon Conjecture.” », The Fibonacci Quarterly, Vol. 10.6,‎ 1972, p. 565–568, 598 (lire en ligne)

[:0-3] (en) David Singmaster, « "Notes on Binomial Coefficients: IV—Proof of a Conjecture of Gould on the G.C.D.'s of Two Triples of Binomial Coefficients." », The Fibonacci Quarterly 11.3,‎ 1973, p. 282-84

[4] (en) Sin Hitotumatu et Daihachiro Sato, « Star of David theorem », Fibonacci Quarterly 13,‎ 1975, p. 70

[Weisstein-5] Weisstein, Eric W. "Star of David Theorem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/StarofDavidTheorem.html

[6] (en) V. E. HOGGATT et W. HANSELL, « THE HIDDEN HEXAGON SQUARES », Fibonacci quarterly vol. 9 n°2,‎ 1971, p. 120,133 (lire en ligne)