Théorème de la moyenne
En analyse réelle, le théorème de la moyenne est un résultat classique concernant l'intégration des fonctions continues d'une variable réelle, selon lequel la moyenne d'une fonction continue sur un segment se réalise comme valeur de la fonction.
Ne doit pas être confondu avec Propriété de la moyenne.
Énoncé
Théorème — Pour toute fonction f à valeurs réelles, définie et continue sur un segment [a , b], avec a < b, il existe un réel c compris entre a et b (a et b étant exclus) vérifiant :
L'intégrale est ici définie au sens de Riemann (mais f étant supposée continue, une forme plus simple d'intégration, comme celle utilisée par Cauchy, peut être employée) ; si on admet le premier théorème fondamental de l'analyse, le théorème de la moyenne se confond avec le théorème des accroissements finis.
On n'en utilise souvent que la conséquence plus faible suivante, connue sous le nom d’inégalité de la moyenne :
(ce dernier résultat est encore valable pour des fonctions intégrables quelconques)
Remarques
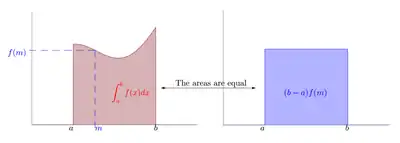
- Graphiquement, une interprétation de ce théorème est que l'aire algébrique sous la courbe représentative de f est égale à celle d'un rectangle de base [a , b], et de hauteur un point moyen de la courbe.
- Ce théorème s'étend aux fonctions réelles de plusieurs variables sur un domaine compact et connexe par les intégrales multiples.
- Le point c ne dépend pas continûment de f.[réf. nécessaire] Le théorème de la moyenne énonce l'existence d'un réel c mais ne donne aucune information sur sa dépendance en la fonction f.
- L'hypothèse de continuité est essentielle. Par exemple pour [a , b] = [0 ; 1] en posant f(x) = 1 si x < 1/2 et f(x) = 0 sinon, la valeur moyenne de f vaut 1/2 donc n'est pas réalisée comme valeur de f.
Démonstration
En utilisant le premier théorème fondamental de l'analyse, ou alors en court-circuitant la théorie de l'intégrale de Riemann et en prenant, comme définition de l'intégrale d'une fonction continue sur un intervalle, la variation sur cet intervalle de l'une quelconque de ses primitives (donc en admettant qu'il en existe), le théorème de la moyenne devient une simple reformulation du théorème des accroissements finis.
En effet, si F est une primitive de f, alors le théorème des accroissements finis pour F fournit l'existence d'un réel c strictement compris entre a et b tel que
ce qui est le résultat souhaité puisque F' = f et
Pour une démonstration plus « directe », cf. généralisation ci-dessous en posant g(x) = 1.
Généralisation
De même que le théorème de la moyenne est une version intégrale du théorème des accroissements finis, sa généralisation suivante est une version intégrale du théorème des accroissements finis généralisé :
Pour toutes fonctions d'une variable réelle f et g continues sur le segment [a, b], avec a < b, g gardant un signe constant sur [a , b], il existe un réel c de ]a , b[ tel que
- Remarque
L'hypothèse que g garde un signe constant est indispensable : par exemple pour [a, b] = [–1, 1] et f(x) = g(x) = x, il n'existe aucun c tel que 2/3 = c × 0.
Articles connexes
- Théorème de moyenne pour les différences divisées (en)
- Intégrale de Stieltjes : première et seconde formules de la moyenne
Lien externe
- Paul Mansion, « Sur le second théorème de la moyenne » (1885), en ligne et commenté sur BibNum.
- Portail de l'analyse