Théorème de réciprocité de Maxwell-Betti
Le théorème de réciprocité de Maxwell-Betti a été énoncé en 1872 par Enrico Betti. Il énonce que
« Si, à un système élastique quelconque, isostatique ou hyperstatique, on applique successivement un premier système de forces, puis après suppression, un second, la somme des travaux du premier système, pour les déplacements élastiques dus aux forces du second, est égale à la somme des travaux des forces du second système pour les déplacements élastiques dus aux forces du premier. »
— B. de Fontviolant, Résistance des Matériaux analytique et graphique[1].
Étant donné que les déformations élastiques sont réversibles, l'énoncé porte sur la comparaison de deux états d'un même système, indépendamment du temps ou de toute précédence. Les travaux d'un système de forces, ou chargement, sous les déplacements dus à l'autre chargement, sont appelés travaux réciproques. On montre que cet énoncé vaut aussi bien pour des couples, qui travaillent sous une rotation, que pour des contraintes travaillant sous un certain champ de déformation[2].
Le théorème de Maxwell-Betti revêt une grande importance en Résistance des Matériaux, surtout dans l'analyse des réseaux de poutres. C'est aussi l'une des sources d'inspiration de la méthode des éléments finis[3]. G. Colonnetti a établi un énoncé voisin par la suite.
Exemples
Résistance des Matériaux
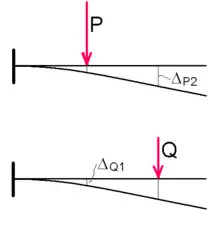
Considérons une poutre horizontale, sur laquelle on choisit deux points 1 et 2 arbitrairement, à cela près qu'ils doivent être distincts des points d'appui (ce qui donnerait, cela dit, un résultat exact, mais trivial). Appliquons une force verticale P au point 1 et notons la flèche au point 2 ; puis, ayant supprimé la charge P, appliquons une force Q au point 2, ce qui produit une flèche au point 1. Le théorème de Maxwell-Betti indique que dans ces conditions :
Système masse-ressort
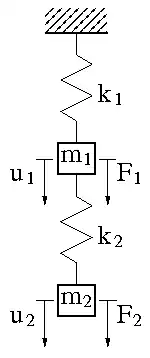
Soient deux masses, de poids respectifs F1 et F2, reliées par deux ressorts de raideurs respectives k1 et k2 et suspendues au plafond du laboratoire. À l'équilibre, l'allongement des ressorts est donné par:
Considérons un premier état, où le poids F1 est négligeable devant F2. Le déplacement sera donné par
Puis un second état, où le poids F2 est négligeable devant F1. Le déplacement sera donné par :
Le théorème de Betti exprime que les déplacements, dans les deux configurations précédentes, sont reliés par :
Le travail s'exprime dans chaque cas par et . En composant ces deux relations, on obtient :
La symétrie de la matrice de raideur K est nécessaire pour que les travaux réciproques soient égaux.
En théorie de l'élasticité
Considérons un solide élastique, occupant un volume V et de surface A extérieure, chargé par des forces de contact et une densité de forces volumiques (par exemple la gravité). Le triplet formé du champ de déplacement, du tenseur des déformations et du tenseur des contraintes définit un état élastique du solide, est associé au chargement extérieur par la conservation de l'énergie mécanique :
Le symbole „“ désigne le produit scalaire de deux vecteurs et le produit doublement contracté « : » (ou « produit de Frobenius »), est une opération entre deux tenseurs A et B que l'on peut définir comme la trace A : B := tr(AT · B). Le travail développé par les forces extérieures et sous le déplacement est donc égal au travail de déformation des contraintes σ sous les déformations ε.
Les déplacements et les déformations dépendent de . Le mot « grad » désigne ici le gradient, et le T en exposant désigne la transposition. Du tenseur de déformation ε, on peut calculer le tenseur des contraintes σ grâce au tenseur d'élasticité symétrique :
Le produit „:“ contracté d'un tenseur de quatrième ordre () avec un tenseur de deuxième ordre (ε) donne un tenseur de deuxième ordre (σ). L'isotropie de comportement dictée par la loi de Hooke donne
Les coefficients sont les Coefficient de Lamé, désigne le tenseur identité de deuxième (resp. de quatrième) ordre tous deux symétriques, de sorte qu'on dispose des identités et . Le théorème de Betti n'exige ni l'isotropie, ni l'homogénéité du matériau.
Soit alors un second état d'équilibre élastique du solide relatif au chargement . Le théorème de Betti énonce que :
La symétrie du tenseur d'élasticité , qui résulte de l'hyperélasticité, constitue une hypothèse essentielle[2].
Théorème du travail maximal
Le théorème de Maxwell-Betti est une conséquence du théorème du travail maximal que nous allons commencer par démontrer.
Soit un champ de déplacement intérieur au solide, et soit le champ de déformation correspondant. Considérons un champ de contrainte , indépendant du champ de déformation précédent, mais satisfaisant à la condition d'équilibre et compatible avec les conditions de chargement de surface , où est le vecteur contrainte développé par le chargement en surface et où est le vecteur normal unité à la surface (dirigé par convention vers l'extérieur et noté avec un ^). Le travail réciproque des contraintes de surfaces sous le champ de déplacement s'exprime avec le tenseur de contrainte :
Si la surface est suffisamment régulière (sans points anguleux), cette intégrale de surface peut être transformée en intégrale de volume grâce au théorème de flux-divergence :
et la formule de Leibnitz donne
En y substituant la conditions d'équilibre et en tenant compte du fait que la composante antisymétrique du gradient de déplacement ne travaille pas dans le produit contracté avec le tenseur (symétrique) des contraintes, c'est-à-dire qu'on a l'identité , on obtient le théorème de l’énergie élastique :
Pour que ce résultat soit valable, il faut[2] que :
- le champ de déplacement soit admissible, c’est-à-dire
- qu’il soit deux fois différentiable dans l’intérieur du solide élastique linéaire, et
- qu’il soit continu ainsi que son gradient dans l'intérieur et à la surface du solide (boule fermée) [V] ;
- et que le tenseur des contraintes soit admissible, c’est-à-dire
- qu’il soit continûment dérivable dans l'intérieur du volume V,
- qu’il soit continu, ainsi que sa divergence, sur le volume fermé [V].
Dans l'énoncé du théorème de l'énergie élastique, le champ de contrainte et le champ de déformation sont mutuellement indépendants et ne sont donc pas nécessairement liés par une loi de comportement. Les forces extérieures exercent donc le même travail sous le champ de déplacement, que les contraintes internes sous le champ de déformation élastique.
Théorème de réciprocité de Maxwell-Betti
Considérons un second état de déformation correspondant à l'action de forces extérieures . Le matériau élastique, en se déformant, développe un champ de contraintes et le déplacement moléculaire un champ de déformation . Comme pour l'état précédent, le théorème de l'énergie élastique s'écrit :
Cette relation reste valable car et sont deux états d'équilibre élastique du solide.
Alors, le tenseur d'élasticité étant symétrique, et de sorte que :
On retrouve bien l'énoncé continu du théorème de Maxwell-Betti :
Là encore, quoique le matériau puisse n'être ni homogène, ni isotrope, la symétrie du tenseur d'élasticité est une condition nécessaire essentielle[2].
Notes
- Chap. XIV Théorèmes découlant de l'équation générale de l’Élasticité, t. I, p. 205.
- M. E. Gurtin et C. Truesdell et S. Flügge (dir.), Handbuch der Physik, vol. VI2/a : The Linear Theory of Elasticity, Springer, (ISBN 3-540-05535-5), p. 98 f
- (de) Thorsten Kunow, « Verbesserte Berechnung von lokalen Zielgrößen mit der Methode der finiten Elemente unter Verwendung von Grundlösungen » [PDF] (consulté le )
Voir également
- Christian La Borderie, Méthodes Énergétiques
- Portail de la physique
- Portail des sciences des matériaux