Théorème japonais de Carnot

Le théorème japonais de Carnot[1] est un théorème de géométrie euclidienne dû à Lazare Nicolas Marguerite Carnot, portant sur une égalité algébrique de distances dans une construction faisant appel au cercle inscrit et au cercle circonscrit à un triangle.

Histoire

En 1800, un samouraï anonyme accrochait au mur d'un temple une tablette de bois sur laquelle était gravé un sangaku, problème de géométrie dédié à une divinité (un kami) et proposé à la sagacité des fidèles. En 1803, Carnot publiait sa Géométrie de position. Hasard de l'Histoire, un théorème de cet ouvrage[2] permet de résoudre élégamment le sangaku précité.

Énoncé

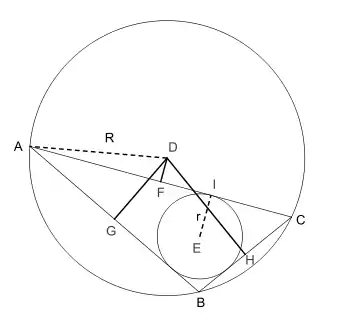
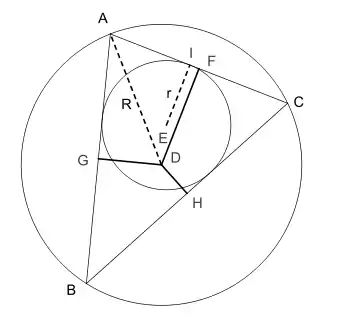
Théorème de Carnot[3]^,[4]^,[5]. — Soit un triangle ABC et son cercle circonscrit de centre D et de rayon R. La somme des distances « signées » du centre D aux côtés du triangle est donnée par :

{\overline {FD}}+{\overline {GD}}+{\overline {HD}}=R+r

où r est le rayon du cercle inscrit au triangle et F, G, H les projetés orthogonaux de D respectivement sur les côtés [AC], [AB] et [BC].

Démonstration .

Triangle obtusangle	Triangle acutangle
$\scriptstyle \|{\overline {GD}}\|+\|{\overline {HD}}\|-\|{\overline {FD}}\|=\|{\overline {AD}}\|+\|{\overline {EI}}\|=R+r$	$\scriptstyle \|{\overline {GD}}\|+\|{\overline {HD}}\|+\|{\overline {FD}}\|=\|{\overline {AD}}\|+\|{\overline {EI}}\|=R+r$

Notes et références

Cet article est partiellement ou en totalité issu de l'article intitulé « Théorème de Carnot » (voir la liste des auteurs).

Daniel Barthe, « Le « théorème japonais » de Lazare Carnot », dans Bibliothèque Tangente, Hors série. n° 24 : Les triangles. Trois points, c'est tout, Pôle Paris, 2005 : sommaire
L. N. M. Carnot, Géométrie de position, J. B. M. Duprat, 1803 (lire en ligne), p. 168
(en) Eric W. Weisstein, « Carnot's Theorem », sur MathWorld
(en) A. Bogomolny, Carnot's Theorem, sur cut-the-knot
(en) Chris Boucher, "Carnot's Theorem", sur le Wolfram Demonstrations Project

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Daniel Barthe, « Le « théorème japonais » de Lazare Carnot », dans Bibliothèque Tangente, Hors série. n° 24 : Les triangles. Trois points, c'est tout, Pôle Paris, 2005 : sommaire

[2] L. N. M. Carnot, Géométrie de position, J. B. M. Duprat, 1803 (lire en ligne), p. 168

[3] (en) Eric W. Weisstein, « Carnot's Theorem », sur MathWorld

[4] (en) A. Bogomolny, Carnot's Theorem, sur cut-the-knot

[5] (en) Chris Boucher, "Carnot's Theorem", sur le Wolfram Demonstrations Project