Théorie de la quantité de mouvement

La théorie de la quantité de mouvement est, en dynamique des fluides, une formulation mathématique de la physique des hélices fondée sur la variation de quantité de mouvement. Elle a été élaborée au XIX^e siècle par William John Macquorn Rankine et Robert Edmund Froude (1889). Cette théorie s’applique aux rotors d’hélicoptères, aux hélices de navire et d'aéronefs, aux éoliennes et hydroliennes.

Hypothèses

La théorie de la quantité de mouvement considère l’hélice comme un disque uniforme. Le disque hélice apparaît comme une hélice possédant une infinité de pales d’épaisseur infiniment petite.

Les hypothèses de la théorie de la quantité de mouvement sont les suivantes :

l’écoulement est irrotationnel ;
le fluide est incompressible ;
le disque hélice ne provoque pas de tourbillon hélicoïdal de sillage ;
le flux est strictement axial et uniforme sur toute la surface du disque hélice ainsi que dans toute section de la veine fluide. Le flux est donc unidirectionnel ;
les forces de friction sont négligées.

Le disque hélice est considéré comme étant en déplacement uniforme et rectiligne dans le fluide de vitesse V à l’infini amont. L’effet principal du disque hélice est l’accélération du fluide à son passage. Cette accélération s’accompagne d’une discontinuité de pression et d’une contraction de la veine fluide. En fait, le disque hélice exerce une poussée T (en anglais : thrust) sur le fluide par la variation de sa quantité de mouvement.

La figure fait apparaître une vitesse V à l’infini amont. Cette vitesse est algébrique — ce qui signifie qu’elle peut être positive (cas des hélices et rotor d’hélicoptère en vol vertical ascendant), nulle (rotor d’hélicoptère en vol stationnaire), ou négative (cas des éoliennes et rotor d’hélicoptère en vol vertical descendant). Dans l’ordre, les cas du vol stationnaire, du vol ascendant puis du vol descendant, seront étudiés respectivement.

Vol stationnaire

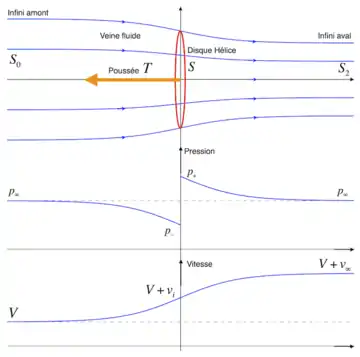
Veine fluide en vol ascendant, variation de pression et de vitesse

$V=0$

La vitesse au passage du disque hélice ${{v}_{i}}$ est appelée vitesse induite. Elle produit ensuite la vitesse ${{v}_{\infty }}$ à l’infini aval. L’équation de conservation de débit s’écrit :

$\rho S{{v}_{i}}=\rho {{S}_{2}}{{v}_{\infty }}$

La poussée est donnée par la variation de quantité de mouvement :

$T=\rho S{{v}_{i}}{{v}_{\infty }}$

La poussée peut également être exprimée en fonction de la discontinuité de pression :

$T=S\left({{p}_{+}}-{{p}_{-}}\right)$

On écrit la relation de Bernoulli en amont et en aval du disque hélice :

${\begin{aligned}&{{p}_{\infty }}={{p}_{-}}+{\frac {1}{2}}\rho v_{i}^{2}\\&{{p}_{+}}+{\frac {1}{2}}\rho v_{i}^{2}={{p}_{\infty }}+{\frac {1}{2}}\rho v_{\infty }^{2}\\\end{aligned}}$

La relation suivante en est déduite :

${{v}_{\infty }}=2{{v}_{i}}$

Démonstration :
Théorème de Bernoulli : ${\frac {v^{2}}{2}}+g\cdot z+{\frac {p}{\rho }}=\mathrm {constante}$ On considère qu'il n'y a de variation d'altitude donc : ${\frac {v^{2}}{2}}+{\frac {p}{\rho }}=\mathrm {constante}$ On obtient donc en amont et en aval du disque hélice : ${\begin{aligned}&{{p}_{\infty }}={{p}_{-}}+{\frac {1}{2}}\rho v_{i}^{2}\\&{{p}_{+}}+{\frac {1}{2}}\rho v_{i}^{2}={{p}_{\infty }}+{\frac {1}{2}}\rho v_{\infty }^{2}\\\end{aligned}}$ En substituant, ${\begin{aligned}&{{p}_{+}}+{\frac {1}{2}}\rho v_{i}^{2}={\frac {1}{2}}\rho v_{\infty }^{2}+{{p}_{-}}+{\frac {1}{2}}\rho v_{i}^{2}\\\\\end{aligned}}$ On réduit : ${\begin{aligned}&{{p}_{+}}={\frac {1}{2}}\rho v_{\infty }^{2}+{{p}_{-}}\\\end{aligned}}$ ${\begin{aligned}\Delta p={\frac {1}{2}}\rho v_{\infty }^{2}\end{aligned}}$ Or, on sait que la poussée peut être donnée soit par la variation de pression, ou soit par la variation de vitesse : $T=\rho S{{v}_{i}}{{v}_{\infty }}$ $T=S\left({{p}_{+}}-{{p}_{-}}\right)$ On obtient : $\rho {{v}_{i}}{{v}_{\infty }}=\Delta p$ On a donc : ${\frac {1}{2}}\rho v_{\infty }^{2}=\rho {{v}_{i}}{{v}_{\infty }}$ On simplifie : ${\frac {1}{2}}v_{\infty }={{v}_{i}}$ L'expression de la poussée donnée par la variation de quantité de mouvement peut être simplifiée : $T=2\rho S{{v}_{i}}^{2}$

Ainsi, la vitesse du sillage à l’infini aval est double de la vitesse induite. On a la relation :

${{v}_{i}}={\sqrt {\frac {T}{2\rho S}}}$

Ainsi, la vitesse induite varie avec la charge surfacique du disque hélice : ${\frac {T}{S}}$ . La puissance nécessaire à l'accélération du fluide est donnée par l’expression

${{P}_{i}}=T{{v}_{i}}$

Cette puissance est appelée puissance induite. On observe aisément que la puissance induite varie avec la vitesse induite et avec la charge surfacique du disque hélice. Il convient de noter que la puissance induite par le vol stationnaire constitue l’essentiel de la puissance requise pour le vol d’un hélicoptère. Il apparaît donc clairement l’importance du dimensionnement du rotor.

Coefficients adimensionnels

Afin d’effectuer des comparaisons pertinentes entre hélices différentes, il convient de définir des coefficients adimensionnels. En ce qui concerne la vitesse, la référence est constituée par la vitesse en bout de pale :

${{v}_{T}}=R\omega$

L’hypothèse d’incompressibilité correspond à la limite du domaine subsonique pour la vitesse en bout de pale. Le coefficient de vitesse induite s’écrit :

${{\lambda }_{i}}={\frac {{v}_{i}}{R\omega }}$

Pour la poussée, on considère une portance uniforme du disque hélice :

${{C}_{T}}={\frac {T}{{\frac {1}{2}}\rho {{\left(R\omega \right)}^{2}}S}}$ où $S=\pi {{R}^{2}}$

On remarquera la présence d’un coefficient ${\frac {1}{2}}$ au dénominateur. Son emploi n’est pas généralisé. En conséquence, on veillera à se rapporter à la définition du coefficient de poussée préalablement à toute comparaison. Toute omission en la matière peut être très ennuyeuse voire fâcheuse.

On obtient les relations :

${\begin{aligned}&{{\lambda }_{i}}={\frac {1}{2}}{\sqrt {{C}_{T}}}\\&{{C}_{T}}=4\lambda _{i}^{2}\\\end{aligned}}$

Un coefficient de puissance induite est défini de même:

${{C}_{Pi}}={\frac {{P}_{i}}{{\frac {1}{2}}\rho {{\left(R\omega \right)}^{3}}S}}$

On a les relations suivantes :

${\begin{aligned}&{{C}_{Pi}}={{C}_{T}}{{\lambda }_{i}}\\&{{C}_{Pi}}={\frac {1}{2}}{{C}_{T}}^{{3}/{2}\;}\\\end{aligned}}$

Vol ascendant

L’équation de conservation de débit s’écrit :

$\rho {{S}_{0}}V=\rho S\left(V+{{v}_{i}}\right)=\rho {{S}_{2}}\left(V+{{v}_{\infty }}\right)$

La variation de quantité de mouvement donne la poussée :

$T=\rho S\left(V+{{v}_{i}}\right){{v}_{\infty }}$

On écrit la relation de Bernoulli en amont et en aval du disque hélice :

${\begin{aligned}&{{p}_{\infty }}+{\frac {1}{2}}\rho {{V}^{2}}={{p}_{-}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}\\&{{p}_{+}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}={{p}_{\infty }}+{\frac {1}{2}}\rho {{\left(V+{{v}_{\infty }}\right)}^{2}}\\\end{aligned}}$

On en déduit la relation :

${{v}_{\infty }}=2{{v}_{i}}$

Démonstration :
On obtient avec le théorème de Bernoulli en amont et en aval du disque hélice : ${\begin{aligned}&{{p}_{\infty }}+{\frac {1}{2}}\rho {{V}^{2}}={{p}_{-}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}\\&{{p}_{+}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}={{p}_{\infty }}+{\frac {1}{2}}\rho {{\left(V+{{v}_{\infty }}\right)}^{2}}\\\end{aligned}}$ En substituant, ${{p}_{+}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}={{p}_{-}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{i}}\right)}^{2}}-{\frac {1}{2}}\rho {{V}^{2}}+{\frac {1}{2}}\rho {{\left(V+{{v}_{\infty }}\right)}^{2}}$ On réduit : $\Delta p={\frac {1}{2}}\rho {{\left(V+{{v}_{\infty }}\right)}^{2}}-{\frac {1}{2}}\rho {{V}^{2}}$ On développe : $\Delta p=\rho V{v}_{\infty }+{\frac {1}{2}}\rho {v}_{\infty }^{2}$ Or, on sait que la poussée peut être donnée soit par la variation de pression, ou soit par la variation de vitesse : $T=\rho S\left(V+{{v}_{i}}\right){{v}_{\infty }}$ $T=S\left({{p}_{+}}-{{p}_{-}}\right)$ On obtient : $\Delta p=\rho \left(V+{{v}_{i}}\right){{v}_{\infty }}$ On a donc : $\rho V{v}_{\infty }+{\frac {1}{2}}\rho {v}_{\infty }^{2}=\rho \left(V+{{v}_{i}}\right){{v}_{\infty }}$ On simplifie : ${\frac {1}{2}}{v}_{\infty }={{v}_{i}}$

On note que cette relation est la même que dans le cas du vol stationnaire. En remplaçant ${{v}_{\infty }}$ dans l’expression de la poussée, il vient :

$T=2\rho S\left(V+{{v}_{i}}\right){{v}_{i}}$

En notant ${{v}_{0}}={\sqrt {\frac {T}{2\rho S}}}$ la vitesse induite donnant la même poussée en vol stationnaire, on calcule :

${\frac {{v}_{i}}{{v}_{0}}}=-{\frac {V}{2{{v}_{0}}}}+{\sqrt {{{\left({\frac {V}{2{{v}_{0}}}}\right)}^{2}}+1}}$

En coefficient adimensionnels, en posant $\mu ={\frac {V}{R\omega }}$ le coefficient de vitesse on obtient :

${\frac {{C}_{P}}{{C}_{T}}}=\mu +{{\lambda }_{i}}$

Notion de rendement propulsif

Dans le cas d’un avion, la puissance utile est :

${{P}_{u}}=TV$

La puissance développée dans ce but est donnée par l’accroissement d’énergie cinétique du fluide, c'est-à-dire la puissance induite :

${{P}_{i}}=T\left(V+{{v}_{i}}\right)$

Le rendement propulsif est défini par :

${{R}_{p}}={\frac {{P}_{u}}{{P}_{i}}}={\frac {2}{1+{\frac {{v}_{i}}{V}}}}={\frac {2}{1+{\sqrt {1+{{C}_{T}}}}}}$

La conséquence est qu’à poussée égale, le rendement maximal sera obtenu lorsque l’accélération de l’air sera minimale, c’est-à-dire le débit maximal. Autrement dit, plus le diamètre de l’hélice sera grand, plus le rendement propulsif sera élevé.

Vol descendant

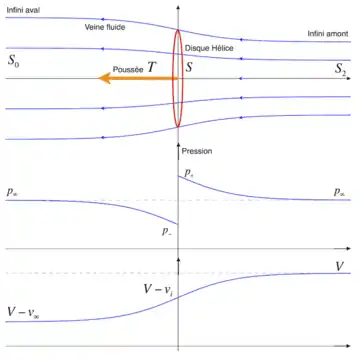
Veine fluide en vol descendant, variation de pression et de vitesse

L’équation de conservation de débit s’écrit :

$\rho {{S}_{0}}\left(V-{{v}_{\infty }}\right)=\rho S\left(V-{{v}_{i}}\right)=\rho {{S}_{2}}V$

La variation de quantité de mouvement donne la poussée :

$T=\rho S\left(V-{{v}_{i}}\right){{v}_{\infty }}$

On écrit la relation de Bernoulli en amont et en aval du disque hélice :

${\begin{aligned}&{{p}_{\infty }}+{\frac {1}{2}}\rho {{V}^{2}}={{p}_{+}}+{\frac {1}{2}}\rho {{\left(V-{{v}_{i}}\right)}^{2}}\\&{{p}_{-}}+{\frac {1}{2}}\rho {{\left(V-{{v}_{i}}\right)}^{2}}={{p}_{\infty }}+{\frac {1}{2}}\rho {{\left(V-{{v}_{\infty }}\right)}^{2}}\\\end{aligned}}$

On en déduit la relation :

${{v}_{\infty }}=2{{v}_{i}}$

Démonstration :
On obtient avec le théorème de Bernoulli en amont et en aval du disque hélice : ${\begin{aligned}&{{p}_{\infty }}+{\frac {1}{2}}\rho {{V}^{2}}={{p}_{+}}+{\frac {1}{2}}\rho {{\left(V-{{v}_{i}}\right)}^{2}}\\&{{p}_{-}}+{\frac {1}{2}}\rho {{\left(V-{{v}_{i}}\right)}^{2}}={{p}_{\infty }}+{\frac {1}{2}}\rho {{\left(V-{{v}_{\infty }}\right)}^{2}}\\\end{aligned}}$ En substituant, ${{p}_{-}}={{p}_{+}}-{\frac {1}{2}}\rho V^{2}+{\frac {1}{2}}\rho {{\left(V-{{v}_{\infty }}\right)}^{2}}$ $\Delta p={\frac {1}{2}}\rho V^{2}-{\frac {1}{2}}\rho {{\left(V-{{v}_{\infty }}\right)}^{2}}$ On développe : $\Delta p=\rho V{v}_{\infty }-{\frac {1}{2}}\rho {v}_{\infty }^{2}$ Or, on sait que la poussée peut être donnée soit par la variation de pression, ou soit par la variation de vitesse : $T=\rho S\left(V-{{v}_{i}}\right){{v}_{\infty }}$ $T=S\left({{p}_{+}}-{{p}_{-}}\right)$ On obtient : $\Delta p=\rho \left(V-{{v}_{i}}\right){{v}_{\infty }}$ On a donc : $\rho \left(V-{{v}_{i}}\right){{v}_{\infty }}=\rho V{v}_{\infty }-{\frac {1}{2}}\rho {v}_{\infty }^{2}$ On simplifie : ${\frac {1}{2}}{v}_{\infty }={{v}_{i}}$

On note que cette relation est la même que dans le cas du vol stationnaire et du vol ascendant. En remplaçant ${{v}_{\infty }}$ dans l’expression de la poussée, il vient :

$T=2\rho S\left(V-{{v}_{i}}\right){{v}_{i}}$

Au vu de ces résultats, il semble que le vol descendant ne présente pas de difficulté particulière dans la mesure où les relations sont similaires à celles du vol ascendant. Cette similarité apparente est trompeuse : en effet, comparons les deux expressions de la poussée :

$T=2\rho S\left(V+{{v}_{i}}\right){{v}_{i}}$

$T=2\rho S\left(V-{{v}_{i}}\right){{v}_{i}}$

En vol ascendant stationnaire, on a :

${\begin{aligned}&V=0\\&{{v}_{i}}={{v}_{0}}={\sqrt {\frac {T}{2\rho S}}}\\\end{aligned}}$

Relation vitesse - vitesse induite

Si l’on remplace ces expressions dans celle de la poussée en vol descendant, on obtient :

$T=-2\rho Sv_{0}^{2}$

Ce qui ne convient pas dans la mesure où la poussée est toujours dirigée vers le haut et positive. Par conséquent, et contrairement au cas du vol ascendant, l’expression de la poussée en vol descendant ne peut pas être étendue au cas du vol stationnaire. Il existe donc un domaine à définir dans lequel la théorie de la quantité de mouvement ne convient pas pour modéliser un vol descendant.

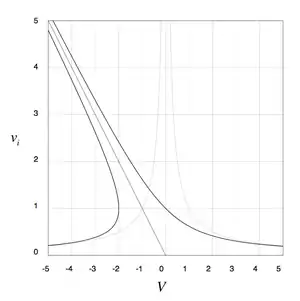
Considérons une vitesse algébrique $V$ (positive en vol ascendant et négative en vol descendant). Introduisons les vitesses adimensionnelles :

${\begin{aligned}&{\bar {V}}={\frac {V}{{v}_{0}}}\\&{{\bar {v}}_{i}}={\frac {{v}_{i}}{{v}_{0}}}\\\end{aligned}}$

On obtient les relations :

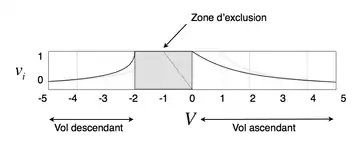
${\begin{aligned}&\left({\bar {V}}+{{\bar {v}}_{i}}\right){{\bar {v}}_{i}}=1\\&\left({\bar {V}}+{{\bar {v}}_{i}}\right){{\bar {v}}_{i}}=-1\\\end{aligned}}$

Domaine de validité de la théorie de la quantité de mouvement

Soit :

${\bar {V}}=\pm {\frac {1}{{\bar {v}}_{i}}}-{{\bar {v}}_{i}}$

La théorie de la quantité de mouvement suppose un flux uniaxial. Or, à proximité de la valeur :

${\bar {V}}=-1$

Il semble qu’il puisse se produire une inversion du sens du flux localement. En conséquence, l’intervalle compris entre $-2$ et $0$ doit être retiré du domaine de validité des formules obtenues :

${\begin{aligned}&\left({\bar {V}}+{{\bar {v}}_{i}}\right){{\bar {v}}_{i}}=1\quad {\bar {V}}\geq 0\\&\left({\bar {V}}+{{\bar {v}}_{i}}\right){{\bar {v}}_{i}}=-1\quad {\bar {V}}\leq -2\\\end{aligned}}$

Liens externes

(en) Momentum theory (Froude) [PDF]

Portail des mathématiques
Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.