Théorie néo-riemannienne
La théorie néo-riemannienne est un ensemble disparate d'idées présentes dans les ouvrages de théoriciens de la musique tels que David Lewin, Brian Hyer, Richard Cohn et Henry Klumpenhouwer. Ce qui rassemble ces idées est une volonté centrale de vouloir mettre les harmonies en relation directe les unes avec les autres sans nécessairement faire référence à une tonique. À l'origine, ces harmonies étaient des accords majeurs et mineurs ; par la suite, la théorie néo-riemannienne a également été étendue à des dissonances. La proximité harmonique est typiquement jugée grâce à la proximité des voix. Ainsi, les accords de do majeur et de mi mineur sont proches de par l'unique demi-ton les séparant. Les mouvements entre les harmonies simples est décrit par des simples transformations. Par exemple, le mouvement entre l'accord de do majeur et de mi mineur, peu importe la direction, est décrit par une transformation « L ». Les progressions étendues sont typiquement représentées sur une surface plane ou une carte, qui décrit l'entièreté du système de relations. En revanche, les idées diffèrent sur ce qui doit être au cœur de la théorie : les voix lisses, les transformations ou la cartographie du système de relations ? La théorie est souvent invoquée lors de l'analyse les coutumes harmoniques du romantisme tardif caractérisées par un degré élevé de chromatisme, y compris dans les œuvres de Schubert, Liszt et Wagner.

Origine
La théorie néo-riemannienne est nommée d'après Hugo Riemann (1849-1919), dont le système 'dualiste' de classification des accords a été adapté des théoriciens du début du XIXe siècle. Le dualisme étant la mise en exergue de la relation inverse entre majeur et mineur, l'un étant l'autre « à l'envers » et inversement. Durant les années 1880, Riemann proposa un système de transformations qui reliait les accords de trois notes directement entre eux. La renaissance de ces idées décrites par Riemann, indépendamment des prémices dualistes sur lesquels elles étaient originellement conçues, commença avec David Lewin (1933-2003), et plus particulièrement dans son article « Amfortas's Prayer to Titurel and the Role of D in Parsifal » (1984) suivi de son livre Generalized Musical Intervals and Transformations (1987). Des développements ultérieurs dans les années 1990 et 2000 ont considérablement étendu le spectre de la théorie néo-riemannienne, avec une systématisation mathématique plus poussée, des incursions dans le répertoire du XXe siècle ou encore dans la psychologie musicale.
Transformations d'accords et conduite des voix
Les principales transformations de la théorie néo-riemannienne connectent des accords de trois notes de différents types (majeurs ou mineurs) à leur inverse (une deuxième application défait la première). Ces transformations sont purement harmoniques et ne nécessitent aucune voix particulière entre les accords : tous les mouvements d'un certain accord donné à un autre accord donné représentent la même transformation néo-riemannienne, peu importe comment les voix sont positionnées dans le registre.
Il existe trois transformations bougeant chacune une des trois notes d'un accord pour en produire un autre :
- La transformation P échange un accord pour son parallèle : le même accord change de mode (exemple : do majeur devient do mineur et inversement). Concrètement, pour un accord majeur, la tierce descend d'un demi-ton et pour un accord mineur, elle monte.
- La transformation R échange un accord pour son relatif : l'accord de l'autre mode mais de même armature (exemple : do majeur devient la mineur et inversement). Concrètement, pour un accord majeur, la quinte monte d'un ton et pour un accord mineur, la fondamentale descend d'un ton.
- La transformation L bouge l'accord d'une tierce majeure en échangeant la fondamentale par la sensible. Concrètement, pour l'accord majeur, la fondamentale descend d'un demi-ton (exemple : do majeur devient mi mineur) et dans un accord mineur, la quinte monte d'un demi-ton (exemple : la mineur à fa majeur).
Des transformations secondaires peuvent également être construites en combinant les transformations de base :
- La transformation N (pour Nebenverwandt) échange un accord majeur par sa sous-dominante mineure ou un accord mineur par sa dominante majeure (exemple : do majeur devient fa mineur et inversement). Cette transformation peut être obtenue en appliquant les transformations R, L puis P.
- La transformation S (pour Slide) échange deux accords partageant une tierce commune (exemple : do majeur et do♯ mineur). Elle peut être obtenue en appliquant L, P et R successivement.
- La transformation H échange un accord par son pole hexatonique (exemple: do majeur et la♭ mineur). Elle peut être obtenue en appliquant les relations L, P puis à nouveau L.
N'importe quelle combinaison de transformations va agir de façon inverse sur les accords majeurs et mineurs : par exemple, les transformations R puis P transposent do majeur d'une tierce mineure, vers la majeur en passant par la mineur, tandis qu'elles vont transformer do mineur en mi♭ mineur en passant par mi♭ majeur et donc monter d'une tierce mineur.
Initialement, la théorie néo-riemannienne traitait ces transformations d'une manière principalement harmonique, sans faire attention à la conduite des voix. Par après, Cohn fit remarquer que la théorie néo-riemannienne surgit naturellement quand on pense à certains problèmes en conduite des voix. Par exemple, deux accords (majeurs ou mineurs) partagent deux notes si et seulement si ils peuvent être liés par une des trois transformations L, P ou R décrites ci-dessus. L'importance accordée aux relations inverses apparaît ici naturellement, comme conséquence d'une conduite des voix rigoureuse, et non comme postulat théorétique fondamental comme ça l'était originellement dans les travaux de Riemann.
Plus récemment, Dmitri Tymoczko a soutenu que le lien entre la théorie néo-riemannienne et la conduite des voix était seulement approximatif.
Représentations graphiques
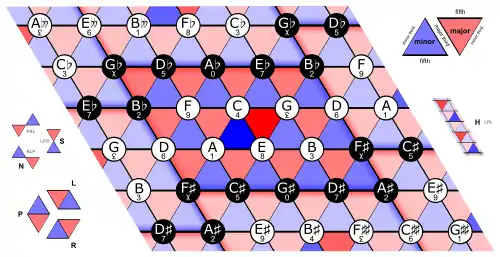
Les transformations néo-riemanniennes peuvent être modélisées par différentes structures géométriques interdépendantes. Le Tonnetz riemannien (grille tonale) est un tableau de tons le long de trois axes simpliciaux, correspondant aux trois intervalles consonants. Les accords majeurs et mineurs sont représentés par des triangles. Les accords adjacents partagent deux notes: les principales transformations sont donc représentées par des mouvements minimums au sein du Tonnetz. Contrairement au théoricien qui a donné son nom à la théorie, la théorie néo-riemannienne considère les équivalences enharmoniques (sol# = la♭), ce qui a comme conséquence d'enrober le graphe planaire dans un tore.

Des géométries tonales alternatives ont été décrites dans la théorie néo-riemannienne qui isolent ou étendent les propriétés du Tonnetz classique. Richard Cohn développa le Système Hyper Hexatonique afin de décrire les mouvements au sein de et entre différents cycles de tierces majeures, ces derniers présentant tous ce qu'il appelle la lisseté maximale (Cohn, 1996). Une autre figure géométrique, la Danse du Cube, a été inventée par Jack Douhett ; c'est le dual géométrique du Tonnetz et représente les accords comme des points discrets et non plus comme des triangles (Douthett et Steinbach, 1998).
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Neo-Riemannian theory » (voir la liste des auteurs).
- Portail de la musique