Tractoire
En mathématiques, les tractoires sont des courbes planes dont le processus de construction est apparenté à celui de la tractrice. Les tractoires constituent des moyens géométriques pour résoudre des équations différentielles. Le mathématicien italien Vincenzo Riccati s'en est servi pour résoudre géométriquement les équations de Riccati.
Tractoire à distance fixe
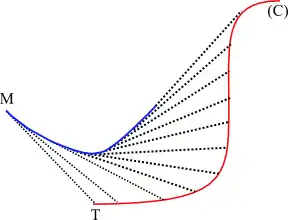
On considère une courbe (C) que l'on appelle la base de la tractoire. Soit d un réel positif. On appelle tractoire de base (C) et de distance d, l'ensemble des points M liés à des points T par les conditions suivantes :
- le point T parcourt la courbe (C)
- la distance MT est égale à d
- la droite (MT) est tangente à la tractoire.
On peut dessiner une tractoire de base (C) en observant le chemin parcouru par un objet M tiré par une ficelle (ou laisse) lorsque l'autre extrémité de la ficelle décrit la courbe (C). C'est le cas par exemple du chemin de la charrue tirée par un bœuf, ou du chemin parcouru par la roue arrière d'un vélo.
Lorsque (C) est une droite, on retrouve la définition de la tractrice.
Tractoire à directrice
Dans la définition précédente, on contraint la longueur MT à rester constante. On contraint donc le point M à rester sur un cercle de centre T et de rayon fixe. On peut généraliser les tractoires en contraignant M à rester sur une courbe (D) définie par rapport au point T et que T entrainerait dans son déplacement. La courbe (D) s'appelle alors la directrice de la tractoire.
Liens externes
- Résolution par des tractoires
- [PDF]Dominique Tournès - La Construction tractionnelle des équations différentielles dans la première moitié du XVIIIe siècle
- Portail de la géométrie