Trapézoèdre
En géométrie, un trapézoèdre ou antidiamant ou deltoèdre n-gonal est le polyèdre dual d'un antiprisme n-gonal régulier. Ses 2n faces sont des deltoïdes isométriques (ou cerfs-volants). Les faces sont décalées symétriquement.
| Antidiamants | |
|---|---|
 | |
| Faces | 2n cerfs-volants |
| Arêtes | 4n |
| Sommets | 2n+2 |
| Configuration des faces | V3.3.3.n |
| Groupe de symétrie | Dnd |
| Polyèdre dual | antiprisme |
| Propriétés | convexe, transitivité sur les faces |
La partie n-gonale du nom ne fait pas référence aux faces mais à l'arrangement des sommets autour d'un axe de symétrie. L'antiprisme dual n-gonal possède deux faces n-gonales.
Un trapézoèdre n-gonal peut être décomposé en deux pyramides n-gonales égales et un antiprisme n-gonal.
Terminologie
Le terme trapézoèdre est trompeur puisque les faces ne sont pas des trapèzes ; le terme alternatif deltoèdre peut être confondu avec celui de deltaèdre désignant une notion différente. Le terme antidiamant est plus utilisé en français[1].
Dans les textes décrivant les habitus en minéralogie, le mot trapézoèdre est souvent utilisé pour faire référence au polyèdre connu sous le nom d'icositétraèdre trapézoïdal.
Formes
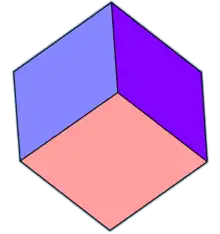
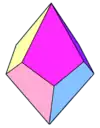
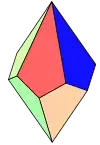
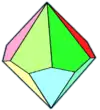
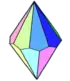

- Le trapézoèdre trigonal - 6 faces (losanges) - dual : octaèdre
- Le cube est un cas particulier de trapézoèdre trigonal, cas où les faces sont carrées.
- Le trapézoèdre trigonal est un cas particulier de rhomboèdre avec des faces losanges isométriques
- Le trapézoèdre tétragonal - 8 faces en cerf-volant - dual : antiprisme carré
- Le trapézoèdre pentagonal - 10 faces en cerf-volant - dual : antiprisme pentagonal
- Le trapézoèdre hexagonal - 12 faces en cerf-volant - dual : antiprisme hexagonal
- Le trapézoèdre heptagonal - 14 faces en cerf-volant - dual : antiprisme heptagonal
- Le trapézoèdre octogonal - 16 faces en cerf-volant - dual : antiprisme octogonal
- Le trapézoèdre ennéagonal - 18 faces en cerf-volant - dual : antiprisme ennéagonal
- Le trapézoèdre décagonal - 20 faces en cerf-volant - dual : antiprisme décagonal
- ...Le trapézoèdre n-gonal - 2n faces en cerf-volant - dual : antiprisme n-gonal
Dans le cas du dual d'un antiprisme régulier triangulaire, les cerfs-volants sont des losanges, par conséquent, ces antidiamants sont aussi des zonoèdres. Ils sont appelés rhomboèdres. Ce sont des cubes allongés dans la direction d'une diagonale. Ce sont aussi des parallélépipèdes avec des faces losanges isométriques.
Un cas particulier de rhomboèdre est celui dont les losanges qui forment les faces ont des angles de 60° et 120°. Il peut être décomposé en deux tétraèdres réguliers égaux et un octaèdre régulier. Puisque les parallélépipèdes peuvent remplir l'espace, une combinaison d'un tétraèdre régulier et d'un octaèdre régulier le fait également.
Exemples
- Les arrangements cristallins des atomes peuvent se répéter dans l'espace avec des cellules trapézoédriques.
- Le trapézoèdre pentagonal est le premier solide différent des solides de Platon utilisé comme un dé dans les jeux de rôle tels que Donjons et Dragons. Ayant 10 côtés, il peut être utilisé en répétition pour générer n'importe quelle probabilité discrète désirée de base décimale.
Symétrie
Le groupe de symétrie d'un trapézoèdre n-gonal est Dnd d'ordre 4n, excepté dans le cas d'un cube, qui possède un groupe de symétrie plus large Od d'ordre 48, qui a quatre versions de D3d comme sous-groupes.
Le groupe de rotation est Dn d'ordre 2n, excepté dans le cas d'un cube, qui possède le groupe de rotation plus large O d'ordre 24, qui a quatre versions de D3 comme sous-groupes.
Voir aussi
Liens externes
- Polyèdres en réalité virtuelle dans l'encyclopédie des polyèdres de G. Hart
- modèles VRML (George Hart) <3> <4> <5> <6> <7> « http://www.georgehart.com/virtual-polyhedra/vrml/octagonal_trapezohedron.wrl%3C8%3E »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) <9> <10>
- Notation de Conway pour les polyèdres Essayer : "dAn", où n=3,4,5... exemple "dA5" est un trapézoèdre pentagonal.
- Robert Ferréol, « Antidiamant », sur Encyclopédie des formes mathématiques remarquables.
- Patron en papier d'un trapézoèdre tétragonal (carré)
Notes et références
- Maurice Starck, « Diamants et antidiamants », sur polyhedra-world.nc (consulté le )
- Portail de la géométrie