Tri à peigne

Le comb sort ou tri à peigne ou tri de Dobosiewicz est un algorithme de tri assez simple initialement inventé par Wodzimierz Dobosiewicz en 1980[2]. Il a été redécouvert et popularisé plus récemment par Stephen Lacey et Richard Box dans un article publié en [3] dans la revue Byte Magazine. Le comb sort améliore notablement les performances du tri à bulles, et peut rivaliser avec des algorithmes de tri réputés rapides comme le tri rapide (quick sort), le tri fusion (merge sort) ou le tri de Shell (Shell sort).

Tri à peigne
Exemple de tri d'une liste de nombres par le tri à peigne.
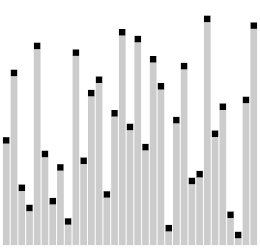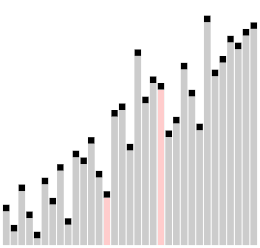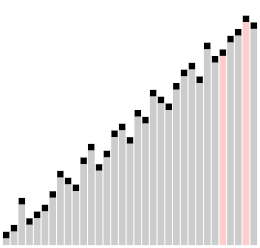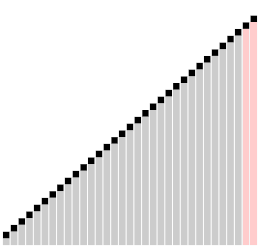
Problème lié
Structure des données
Complexité en temps
Pire cas
[1]
Meilleur cas
Complexité en espace
Pire cas

Dans le tri à bulles ascendant classique[4], chacun des éléments de la liste à trier est comparé avec son voisin immédiat et interverti s'il est plus grand que l'élément suivant. Dans ce type de tri, les grandes valeurs situées à l'origine près du début de la liste à trier montent rapidement vers la fin de la liste (on parle de « lièvres »), alors que les petits éléments proches de la fin de la liste ne redescendent que très lentement vers le début de la liste (ce sont les « tortues »). C'est l'existence de ces « tortues » qui pénalise fortement les performances du tri à bulles. L'idée de base est d'éliminer ces « tortues » (les « lièvres » ne posent pas de problème de performance) en les déplaçant plus rapidement vers le début de la liste. L'amélioration apportée par le comb sort au tri à bulles est analogue à celle qu'apporte le tri de Shell[5],[6] au tri par insertion. Robert Sedgewick, l'un des spécialistes les plus réputés des algorithmes de tri, inverse en quelque sorte le point de vue en considérant (dans certains au moins de ses écrits) le comb sort comme une variante du tri de Shell qui utiliserait le tri à bulles comme algorithme de départ[7].

L'idée de base du comb sort est de comparer un élément avec un autre élément plus lointain, espacé de celui-ci d'un certain intervalle. Au départ, cet intervalle est relativement grand, puis on le réduit progressivement à chaque passe de l'algorithme jusqu'à ce qui ne soit plus que de 1 en fin de traitement. Le tri à bulles peut être considéré comme une variante du comb sort dans lequel l'intervalle est toujours de 1.

Autrement dit, la boucle interne du tri à bulle (celle qui fait la comparaison de deux éléments voisins et l'échange des valeurs si nécessaire) est modifiée pour comparer d'abord des éléments distants de la valeur de l'intervalle, puis, à chaque passe, cet intervalle est divisé par un certain coefficient, le facteur de réduction jusqu'à ce qu'il tombe à 1.

La valeur d'origine de l'intervalle est généralement la taille de la liste à trier divisée par le facteur de réduction. Des essais empiriques ont montré que la valeur idéale de ce facteur de réduction est voisine de 1,3 (voir ci-dessous).

Formulation en pseudocode

Le tri par peigne peut se formuler en pseudo-code de la façon suivante :

fonction combsort(tableau liste)
    intervalle := liste.taille //initialisation de l'intervalle
    
    Répéter tant que intervalle > 1 ou échange = vrai
        intervalle := int(intervalle / 1.3)
        si intervalle < 1
          intervalle := 1
        fin si
        
        i := 0
        échange := faux
        
        Répéter tant que i < liste.taille - intervalle
            si liste[i] > liste[i + intervalle]
                échanger liste[i] et liste[i + intervalle]
                échange := vrai
            fin si
            i := i + 1
        fin tant que
       
    fin tant que
fin fonction

Facteur de réduction

Le choix du facteur de réduction a un impact élevé sur l'efficacité du comb sort. Dans l'article d'origine, les auteurs proposaient une valeur de ou 1,3.

Une valeur trop petite ralentit l'algorithme parce qu'il faut effectuer plus de comparaisons, alors qu'une valeur trop grande signifie que toutes les tortues ne sont pas éliminées lorsque l'intervalle est réduit à 1, ce qui conduit à plusieurs passes d'un tri à bulles pour compléter le tri. La valeur idéale est sans doute un compromis entre ces deux écueils.

Des auteurs ont proposé d'autres valeurs, telles que comme facteur de réduction (avec égal au nombre d'or, soit environ 1,618034). D'autres auteurs ont proposé 1,2796. Des essais extensifs semblent indiquer que tout facteur de réduction inférieur à suffise à éliminer toutes les tortues, mais cette conjecture paraît difficile à prouver rigoureusement. Dans tous les cas, il semble bien que la valeur idéale soit située quelque part entre 1,25 et 1,33. On choisira une valeur arbitraire de 1,3 pour la suite de cet article.

Propriétés de l'algorithme

Le comb sort est un tri "en place" (voir Caractère en place), c'est-à-dire qu'il peut trier les éléments d'un tableau à l'intérieur même de ce tableau, sans devoir allouer de structures de mémoire supplémentaires pour stocker des résultats temporaires. Il est donc peu gourmand en mémoire. De même, contrairement à plusieurs algorithmes de tri rapides, il n'est pas récursif et ne génère donc pas non plus d'occupation mémoire implicite sur la pile d'exécution. Ces propriétés peuvent être intéressantes quand il s'agit de trier de gros volumes de données s'approchant des capacités mémoires de la machine utilisée.

C'est un algorithme instable (voir Caractère stable), c'est-à-dire que si deux enregistrements ont la même clef de tri, il ne garantit pas que les enregistrements se retrouveront dans le même ordre qu'au départ. Toutefois, il est toujours possible de transformer un tri instable en un tri stable, moyennant l'utilisation de O(n) mémoire supplémentaire pour stocker l'ordre initial des éléments.

Comme le tri de Shell, sa complexité algorithmique théorique est très délicate à analyser. On peut facilement montrer qu'elle est au pire de O(n2), mais elle est bien meilleure en réalité, sans que l'on parvienne à le démontrer théoriquement.[8] Dans la pratique (et moyennant le choix d'un Facteur de réduction approprié), il se comporte de la même façon que les algorithmes de tris connus pour être en O(n log n) dans tous les cas, comme le tri fusion.

Variantes

Comb sort 11

Avec un facteur de réduction de l'ordre de 1,3, il n'y a que trois manières possibles de terminer la liste des intervalles : (9, 6, 4, 3, 2, 1), (10, 7, 5, 3, 2, 1), ou (11, 8, 6, 4, 3, 2, 1). Les expériences ont montré que l'on obtenait une amélioration notable de la vitesse en choisissant un intervalle de 11 lorsque la valeur calculée serait sinon de 9 ou 10. Cette variante est appelée « comb sort 11 ».

Si l'on utilisait l'une des séquences commençant à 9 ou 10, la passe finale avec un intervalle de 1 a moins de chance de trier complètement les données, ce qui nécessite alors au moins une passe supplémentaire avec un intervalle de 1. Les données sont complètement triées quand aucun échange n'a lieu au cours d'une passe avec un intervalle de 1.

Comb sort se terminant par une autre méthode de tri

Comme de nombreux autres algorithmes de tri (par exemple le tri rapide ou le tri fusion), le comb sort est plus efficace dans ses premières passes que dans les dernières, quand il se réduit à un tri à bulles. On peut améliorer les performances du comb sort en changeant de méthode de tri quand l'intervalle devient suffisamment petit (par exemple inférieur à 10). On peut par exemple passer au Tri cocktail ou, mieux à un tri par insertion[9].

Un autre avantage de cette méthode est qu'il n'est pas nécessaire de vérifier si un échange a eu lieu au cours de la passe pour savoir s'il faut arrêter le tri.

Exemples

Perl

 
sub comb_sort {
  my @v = @_;
  my $max = scalar (@v);
  my $gap = $max;
  while (1) {
     my $swapped = 0;
     $gap = int ($gap / 1.3);
     $gap = 11 if $gap == 10 or $gap == 9; # (optimisation Combsort11)
     $gap = 1 if $gap < 1;
     my $lmax = $max - $gap - 1;
     foreach my $i (0..$lmax) {
          ($v[$i], $v[$i+$gap], $swapped) = ($v[$i+$gap], $v[$i], 1) if $v[$i] > $v[$i+$gap];
     }
     last if $gap == 1 and $swapped == 0;
  }
  return @v;
}

Notes et références
  1. (en) Bronislava Brejová, « Analyzing variants of Shellsort », Information Processing Letters, Elsevier, vol. 79, no 5,‎ , p. 223-227 (ISSN 0020-0190 et 1872-6119, OCLC 38995181, DOI 10.1016/S0020-0190(00)00223-4)
  2. W. Dobosiewicz. An efficient variation of bubble sort. Information Processing Letters 11, 1980, 5–6.
  3. http://cs.clackamas.cc.or.us/molatore/cs260Spr03/combsort.htm
  4. Robert Sedgewick. Algorithms, Addison Wesley, 1983, p. 99. ISBN O-201-06672-6.
  5. D. Shell. A high-speed sorting procedure Communications of the ACM 2, 1959, 30–32
  6. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. (ISBN 0-262-03293-7).
  7. Analysis of Shellsort and Related Algorithms, Robert Sedgewick, Fourth European Symposium on Algorithms, Barcelona, September 1996
  8. Brejová, Bronislava, Analyzing variants of Shellsort.
  9. Donald Knuth, The Art of Computer Programming, vol. 3 : Sorting and Searching, 1973, exercise 5.2.1-40.

Liens externes
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.