Tri de crêpes

Le tri de crêpes (de l'anglais pancake sorting) est un problème mathématique. Il s'agit de trier une pile de crêpes afin que les crêpes soient empilées de la plus grande à la plus petite (au sens de leur diamètre). La seule opération autorisée pour arriver à ce résultat est de retourner la partie supérieure de la pile. On peut considérer d'une part le problème algorithmique, où le but est d'arriver à la configuration finale, comme pour un algorithme de tri, et d'autre part des questions mathématiques. Une question classique est d'évaluer le nombre minimum de mouvements nécessaires, pour toute pile d'une certaine taille.

Tri de crêpes
Rotation d'une partie de la pile de crêpes à l'aide de la spatule.
Problème lié

Contexte

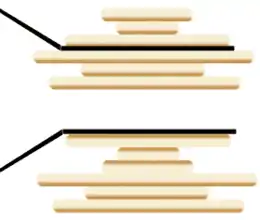
Un cuisinier fait des crêpes et les pose en pile à côté de la poêle lorsqu'elles sont cuites. Toutes les crêpes sont de taille différente. On dispose donc d'une pile de crêpes, chacune de taille différente et il s'agit d'ordonner les crêpes dans la pile, par ordre décroissant de taille (diamètre) avec donc celle de plus petit diamètre en haut de la pile. Un seul type d'opération est autorisé pour manipuler la pile : insérer une spatule à un endroit de la pile et retourner d'un coup toutes les crêpes qui se trouvent au-dessus de la spatule.

Problèmes mathématiques

La question est : pour N crêpes, quel est le nombre minimum de manipulations (P) qui sont nécessaires pour mettre toute pile dans l'ordre décroissant ?

Un premier exemple peut être avec 2 crêpes (N=2), où l'on a alors seulement deux configurations de pile possibles. Soit il a cuit d'abord la petite puis la plus grande, soit c'est le contraire. Dans le premier cas, la plus petite est en bas et la plus grande en haut : il faut donc retourner toute la pile pour la mettre dans l'ordre voulu en glissant la spatule sous la crêpe du fond de la pile. Une seule manipulation est ainsi nécessaire. Dans le second cas, la pile est déjà dans l'ordre désiré, aucune manipulation n'est nécessaire. Donc pour N=2, P est au maximum de 1.

Le nombre minimum de manipulations est toujours 0 puisque le cuisinier peut avoir cuit les crêpes dans l'ordre décroissant de taille, auquel cas il n'y a aucune manipulation à faire. D'autre part, dès que N>4, il existe des piles où aucune crêpe ne touche une crêpe qui sera sa voisine dans le tri final (paire adjacente de crêpes). Comme chaque inversion crée au plus une adjacence de ce type, le tri prend nécessairement au moins N inversions - mais peut devoir en prendre plus[1]. De même, le nombre maximal est toujours inférieur à 2N-3 (on peut trier la pile séquentiellement, en commençant par la plus grande, avec deux inversions par crêpes, et le tri des deux dernières prend au plus un coup)[1]. Mais cette manière de faire n'est pas nécessairement optimale. Si une pile de trois crêpes peut demander jusqu'à trois inversions, une pile de quatre peut toujours être triée en quatre inversions (économisant un coup) et une pile de cinq en cinq inversions (économisant deux coups).

P en fonction de N

Le problème qui se pose est de trouver la loi mathématique qui donne P pour tout N, quand le tri est conduit de manière optimale. Ce problème est NP-difficile[2],[3] et n'a toujours pas de solution complète. Les chercheurs qui se penchent depuis plus de 30 ans sur la question ont jusqu'ici réussi à estimer P qui serait toujours inférieur à [2]. Cette valeur a été révélée en 2008 par une équipe de l'Université de Dallas (Texas). Cette valeur affine un majorant de obtenu en 1979[1].

Nombre de problèmes

Le nombre C de configurations qu’une pile de crêpes possède au début du problème dépend du nombre N de crêpes dans cette pile. Il s’agit du nombre de façons différentes de permuter les N crêpes, soit une simple factorielle : C = N !. Pour chaque configuration de départ, il faut un nombre minimum P de manipulations au minimum afin de trier la pile. Bien qu’encore impossible de déterminer P pour tout N, on connaît toutefois le nombre de problèmes nécessitant P manipulations, pour un nombre de crêpes N fixé.

  • Pour une pile d’une crêpe (N=1), il n’y a qu’une seule configuration possible (C=1). On peut considérer que la « pile » est déjà triée.
  • Pour une pile de deux crêpes (N=2), il y a deux configurations possibles (C=2) :
    • la crêpe du dessus est plus petite que celle du dessous : la pile est déjà triée et ne nécessite donc aucune manipulation (P=0)
    • le diamètre de la crêpe du dessus est plus large que celle du dessous : il faut retourner toute la pile en une manipulation (P=1)
  • Pour une pile de trois crêpes (N=3), il y a six configurations possibles (C=6) :
    • une configuration pour laquelle la pile est déjà triée, ne nécessitant aucune manipulation (P=0). On peut noter cette pile de la façon suivante : {1 ; 2 ; 3}.
    • deux configurations pour lesquelles il faut une seule manipulation (P=1). Il s’agit de la pile {2 ; 1 ; 3} où il faut retourner les deux premières crêpes et de la pile {3 ; 2 ; 1} où il faut retourner la pile complète.
    • deux configurations pour lesquelles il faut deux manipulations (P=2). Il s’agit des piles {2 ; 3 ; 1} et {3 ; 1 ; 2}.
    • une configuration nécessitant trois manipulations (P=3). Il s’agit de la pile {1 ; 3 ; 2}.

Le tableau suivant donne le nombre de problèmes nécessitant P manipulations, pour un nombre de crêpes N donné.

Nombre de piles de taille donnée nécessitant P manipulations pour être triée
Nombre P de manipulations nécessaires
01234567891011121314
Nombre N
de crêpes		1 1
2 11
3 1221
4 136113
5 1412354820
6 1520791992811332
7 16301495431 3571 9031 01635
8 17422511 1914 28110 56115 0118 520455
9 18563912 27810 66638 01593 585132 69779 3795 804
10 19725753 96322 825106 461377 863919 3651 309 756814 67873 232
11 110908096 42943 891252 7371 174 7664 126 5159 981 07314 250 4719 123 648956 3546
12 1111101 0999 88377 937533 3973 064 78814 141 92949 337 252118 420 043169 332 213111 050 06613 032 704167
Tri d’une pile de 6 crêpes. Il s’agit de la configuration {5 ; 3 ; 6 ; 1 ; 4 ; 2}, l’une des deux piles de 6 crêpes nécessitant 7 manipulations (l’autre étant {4 ; 6 ; 2 ; 5 ; 1 ; 3}).

Ce tableau, lu ligne par ligne, constitue la suite A092113 de l'OEIS.

Intérêts

Dans un autre formalisme, le problème est équivalent au tri d'un tableau à l'aide d'une seule opération, l'inversion d'un préfixe.

Le tri de crêpes présenté en parallèle du problème classique du tri permet d'insister sur les opérateurs permis pour résoudre un problème d'algorithmique.

Une des particularités de ce tri se trouve dans les personnes s'y étant initialement intéressées : Bill Gates (fondateur de Microsoft, qui avait publié sous son vrai nom William Gates), David X. Cohen (l'un des créateurs de la série Futurama), et aussi Christos Papadimitriou, un informaticien de grand renom[2].

Sources

Références
  1. Gates et Papadimitriou 1979
  2. Jérôme Cottanceau, Le choix du meilleur urinoir : Et 19 autres problèmes amusants qui prouvent que les maths servent à quelque chose !, Paris, Belin, coll. « Science à plumes », , 216 p. (ISBN 978-2-7011-9766-1), chap. 19 (« À quoi servent les maths... À trier ses crêpes comme Bill Gates ? »).
  3. (en) Laurent Bulteau, Guillaume Fertin et Irena Rusu, « Pancake Flipping is hard », Journal of Computer and System Sciences, vol. 81, no 8,‎ (lire en ligne).

Articles scientifiques

Vulgarisation
  • Jérôme Cottanceau, Le choix du meilleur urinoir : Et 19 autres problèmes amusants qui prouvent que les maths servent à quelque chose !, Paris, Belin, coll. « Science à plumes », , 216 p. (ISBN 978-2-7011-9766-1), chap. 19 (« À quoi servent les maths... À trier ses crêpes comme Bill Gates ? »).

Liens

Articles connexes

Liens externes
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.