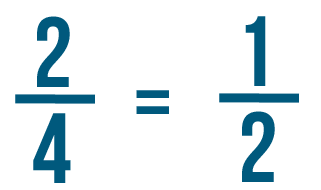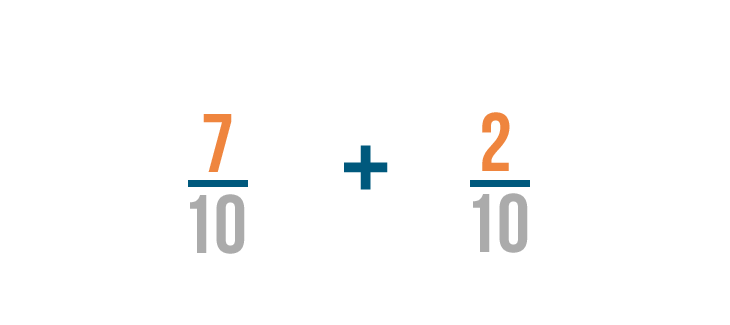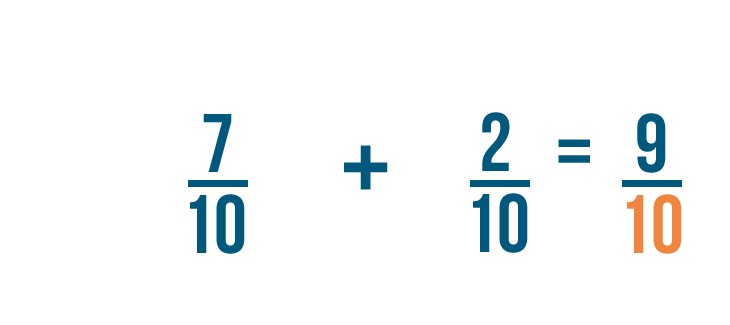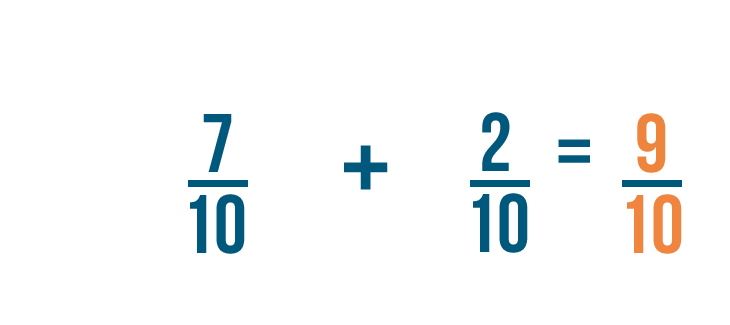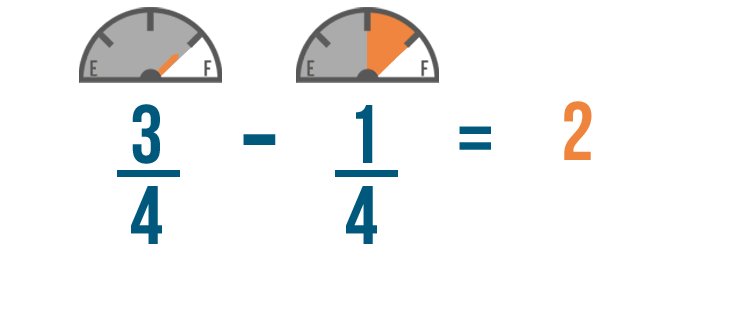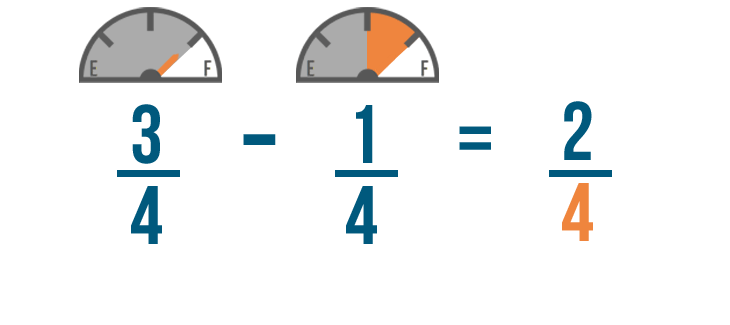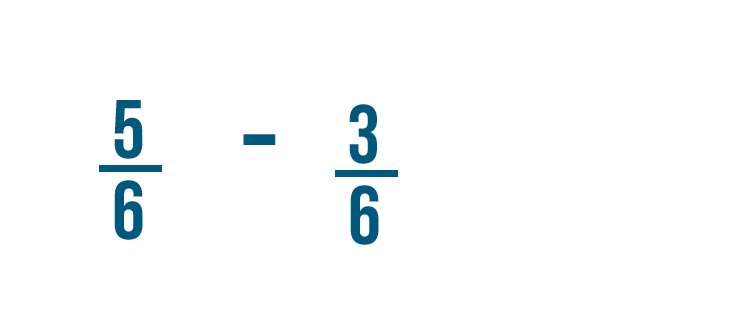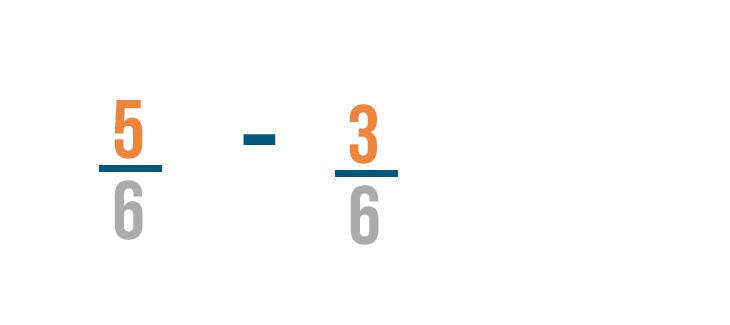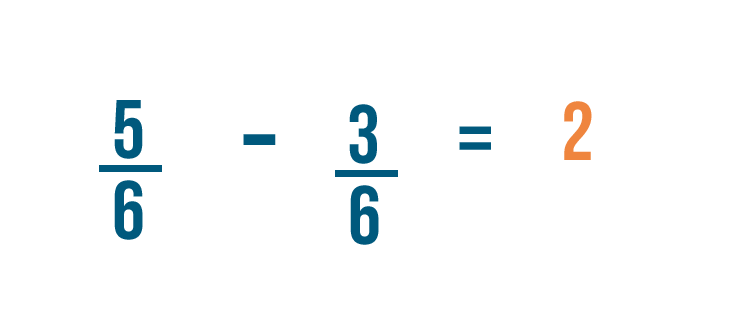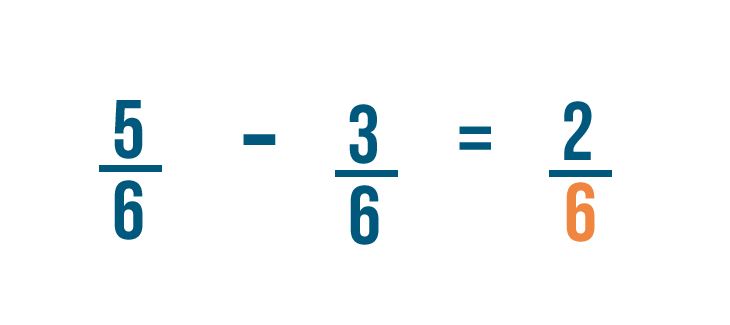Solving addition problems with fractions
Now that we know how to write addition problems with fractions, let's practice solving a few. If you can add whole numbers, you're ready to add fractions.
Click through the slideshow to learn how to add fractions.

Let's continue with our previous example and add these fractions: 3/5 of cup of oil and 1/5 of a cup of oil.
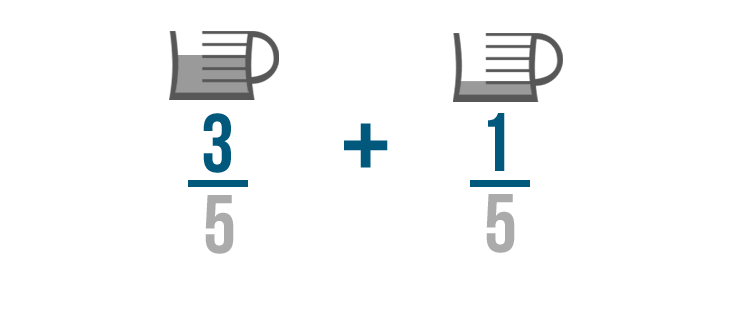
Remember, when we add fractions, we don't add the denominators.

This is because we're finding how many parts we need total. The numerators show the parts we need, so we'll add 3 and 1.
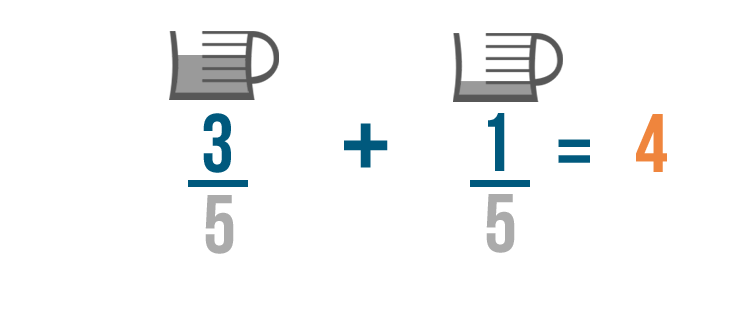
3 plus 1 equals 4. Make sure to line up the 4 with the numbers you just added.
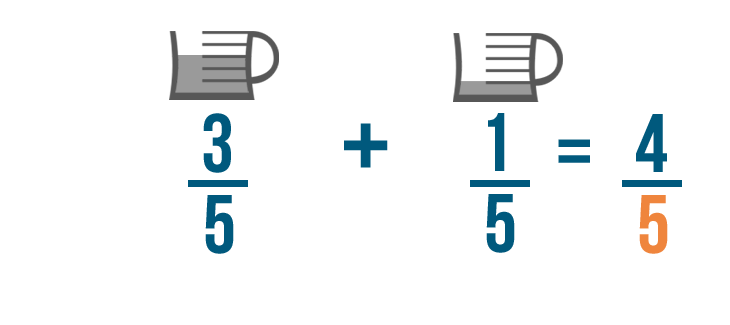
The denominators will stay the same, so we'll write 5 on the bottom of our new fraction.
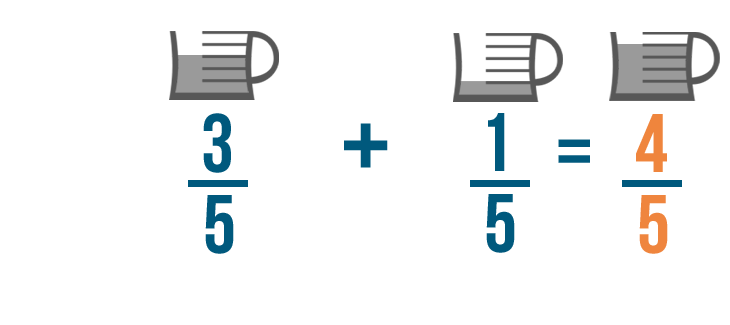
3/5 plus 1/5 equals 4/5. So you'll need 4/5 of a cup of oil total to make your cake.

Let's try another example: 7/10 plus 2/10.
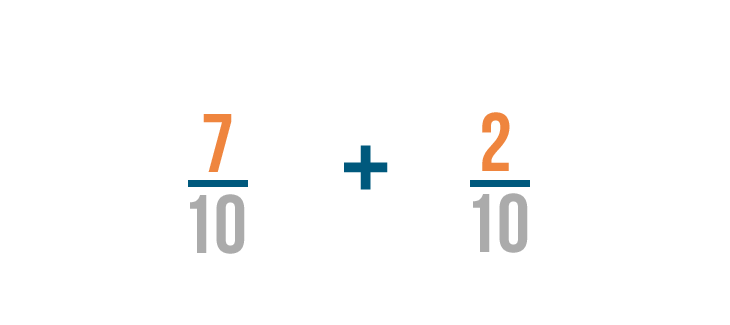
Just like before, we're only going to add the numerators. In this example, the numerators are 7 and 2.

7 plus 2 equals 9, so we'll write that to the right of the numerators.
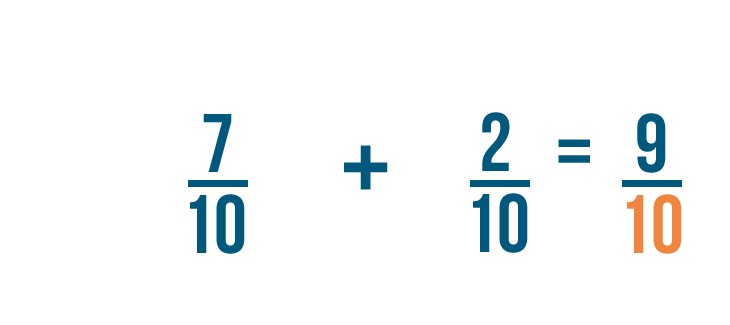
Just like in our earlier example, the denominator stays the same.
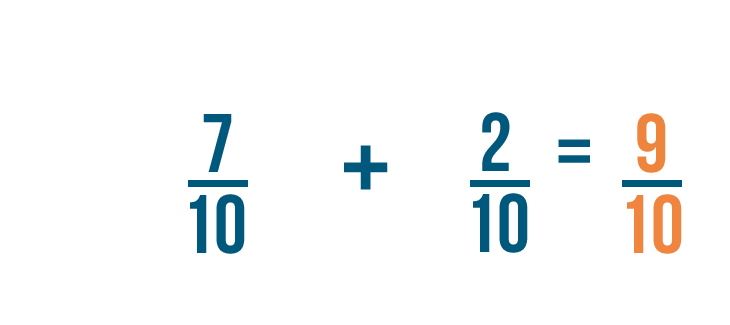
So 7/10 plus 2/10 equals 9/10.

Now it's your turn! Try solving some of the addition problems below.
Solving subtraction problems with fractions
Subtracting fractions is a lot like regular subtraction. If you can subtract whole numbers, you can subtract fractions too!
Click through the slideshow to learn how to subtract fractions.

Let's use our earlier example and subtract 1/4 of a tank of gas from 3/4 of a tank.
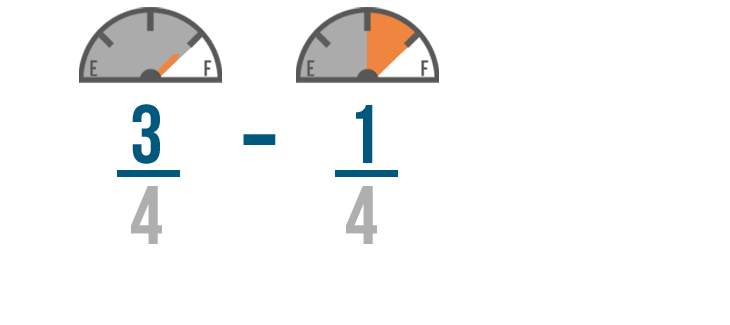
Just like in addition, we're not going to change the denominators.
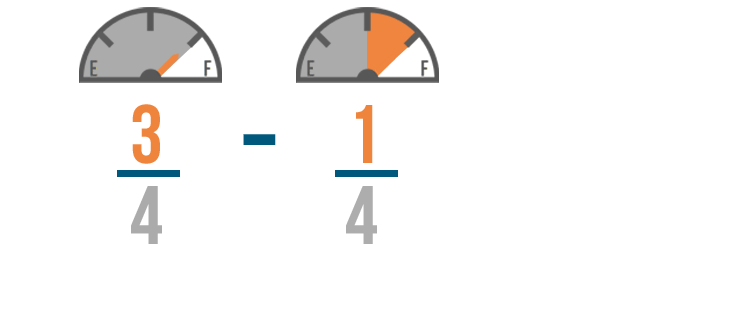
We don't want to change how many parts make a whole tank of gas. We just want to know how many parts we'll have left.
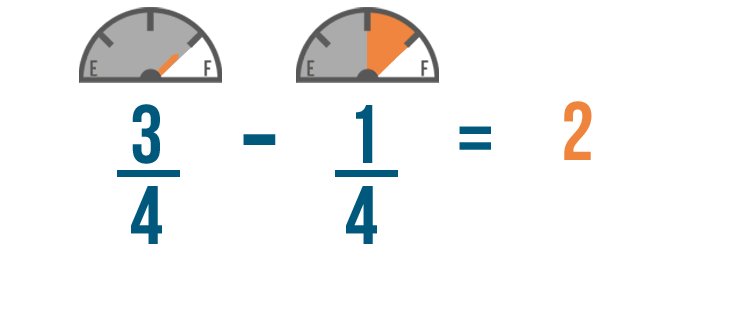
We'll start by subtracting the numerators. 3 minus 1 equals 2, so we'll write 2 to the right of the numerators.
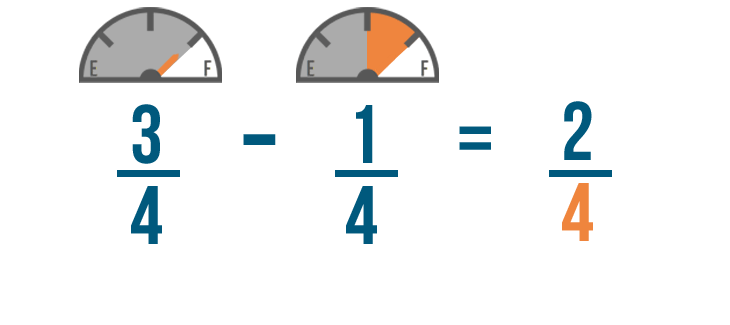
Just like when we added, the denominator of our answer will be the same as the other denominators.

So 3/4 minus 1/4 equals 2/4. You'll have 2/4 of a tank of gas left when you get home.
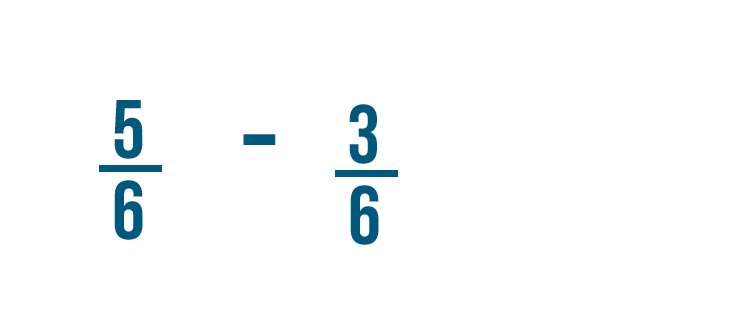
Let's try solving another problem: 5/6 minus 3/6.
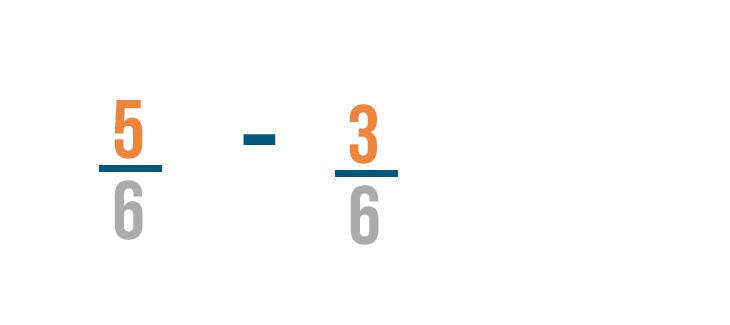
We'll start by subtracting the numerators.
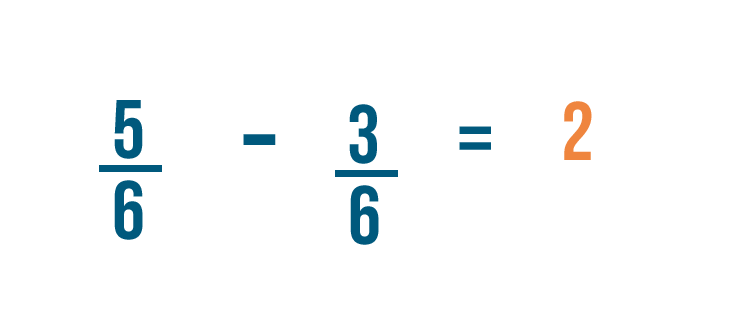
5 minus 3 equals 2. So we'll put a 2 to the right of the numerators.
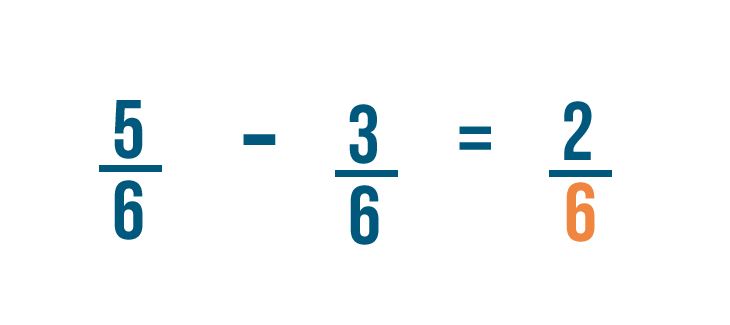
As usual, the denominator stays the same.

So 5/6 minus 3/6 equals 2/6.

Now you try it! Try solving some of the subtraction problems below.
After you add or subtract fractions, you may sometimes have a fraction that can be reduced to a simpler fraction. As you learned in Lesson 2, it's always best to reduce a fraction to its simplest form when you can. For example, 1/4 plus 1/4 equals 2/4. Because 2 and 4 can both be divided 2, we can reduce 2/4 to 1/2.