The generalized Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Stokes' theorem says that the integral of a differential form
The Kelvin–Stokes theorem, also known as the curl theorem, is a theorem in vector calculus on
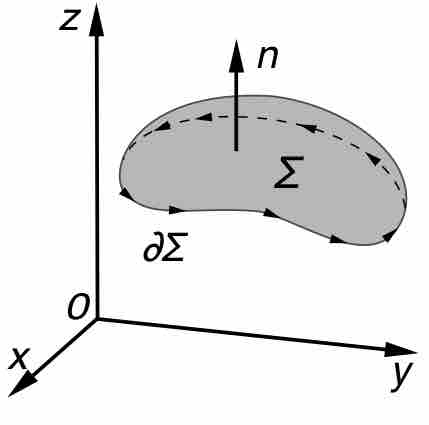
Kelvin-Stokes' Theorem
An illustration of the Kelvin–Stokes theorem, with surface
Application in Electromagnetism
Electric field is a conservative vector field. Therefore, electric field can be written as a gradient of a scalar field:
Applying the Kelvin-Stokes theorem and substituting in
Since
As we have seen in our previous atom on gradient theorem, this simply means:
which is equivalent to saying that work done by the electric field only depends on the initial and final point of the motion. The scalar field