Arc Length and Speed

Arc Length and Speed

Since length is a magnitude that involves position, it is easy to deduce that the derivative of a length, or position, will give you the velocity—also known as speed—of a function. This is because a derivative gives you a rate of change with respect to a parameter. Velocity is the rate of change of a position with respect to time. Let's start this atom by looking at arc length with calculus.

Arc Length

The arc length is the length you would get if you took a curve, straightened it out, and then measured the length of that line . The arc length can be found using geometry, but for the sake of this atom, we are going to use integration. The arc length is approximated by connecting a finite number of points along and curve, connecting those lines to create a a string of very small straight lines, and adding them together. To find this using integration, we should start out by using the Pythagorean Theorem for length of the different sides of a triangle:

 $\displaystyle{ds^2=dx^2+dy^2 \frac{ds^2}{dx^2}\\ \, \quad= 1+\frac{dy^2}{dx^2}ds \\ \, \quad=\sqrt{1+{\frac{dy^2}{dx^2}^2}} \cdot dx\\ \, \quad=\int^b_a\sqrt{1+f'(x)^2} \cdot dx}$

where $s$ is the arc length. If $x=X(t)$ and $y=Y(t)$,

$\displaystyle{s =\int^b_a\sqrt{1+{f'(x)}^2} \cdots dx\\ \,\,=\int^b_a\sqrt{[X'(t)]^2+[Y'(t)] \cdots dt}\\ \,\,= \int^b_a\sqrt{dx^2+dy^2}\\ \,\,= \int^b_a\sqrt{\frac{dx}{dt}^2+\frac{dy}{dt}^2 \cdots dt}}$

Since this is a function of position and is defined by x, we need to have a derivative that is in respect to x:

$\int^b_a\sqrt{1+\frac{dy}{dx}^2*dx}$

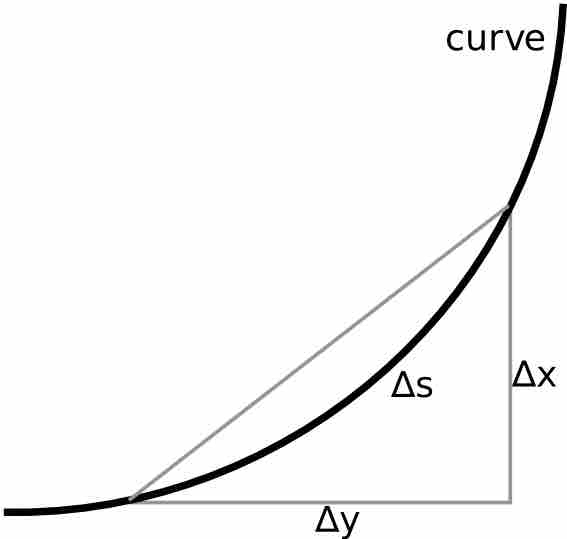
Curves and the Pythagorean Theorem

For a small piece of curve, ∆s can be approximated with the Pythagorean theorem.

Arc Length

The arc length is the equivalent of taking a curve, straightening it out, and then measuring it, as seen in this animation.

Obviously some cases require polar coordinates instead of Cartesian. In polar coordinates:

$r=f(\theta)$

Arc Speed

Now that the hard part is over, we can easily find the speed along this curve. Since speed is in relation to time and not position, we need to revert back to the arc length with respect to time:

$\displaystyle{\int^b_a\sqrt{\frac{dx}{dt}^2+\frac{dy}{dt}^2\cdot dt}}$

Then, differentiate with respect to time:

$\displaystyle{v(t)=s'=\sqrt{[X'(t)]^2+[Y'(t)]^2}}$