Tangent Vectors and Normal Vectors

In order for a vector to be normal to an object or vector, it must be perpendicular with the directional vector of the tangent point. The intersection formed by the two objects must be a right angle.

Normal Vectors

An object is normal to another object if it is perpendicular to the point of reference. That means that the intersection of the two objects forms a right angle. Usually, these vectors are denoted as $\mathbf{n}$.

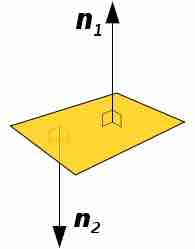
Figure 1: Normal Vector

These vectors are normal to the plane because the intersection between them and the plane makes a right angle.

Not only can vectors be ‘normal' to objects, but planes can also be normal.

Figure 2: Normal Plane

A plane can be determined as normal to the object if the directional vector of the plane makes a right angle with the object at its tangent point. This plane is normal to the point on the sphere to which it is tangent. Each point on the sphere will have a unique normal plane.

Dot Product

As we covered in another atom, one of the manipulations of vectors is called the Dot Product. When you take the dot product of two vectors, your answer is in the form of a single value, not a vector. In order for two vectors to be normal to each other, the dot product has to be zero.

$\mathbf{a} \bullet \mathbf{b} = 0\\ \,\,\,\quad = a_1b_1+a_2b_2+a_3b_3\\ \,\,\,\quad = \left|\mathbf{a}\right| \left|\mathbf{b}\right| \cos \theta$

Tangent Vectors

Tangent vectors are almost exactly like normal vectors, except they are tangent instead of normal to the other vector or object. These vectors can be found by obtaining the derivative of the reference vector, $\mathbf{r}(t)$:

$\mathbf{r}(t) = f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}$