Limits

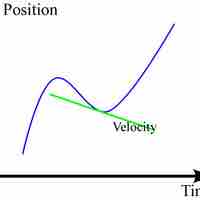
Iinstantaneous velocity can be obtained from a position-time curve of a moving object.

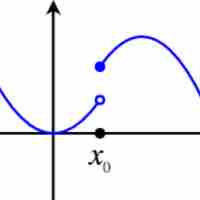
The limit of a function is a fundamental concept in calculus and analysis concerning the behavior of a function near a particular input.

Limits of functions can often be determined using simple laws, such as L'Hôpital's rule and squeeze theorem.

The $(\varepsilon,\delta)$-definition of limit (the "epsilon-delta definition") is a formalization of the notion of limit.

A continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output.

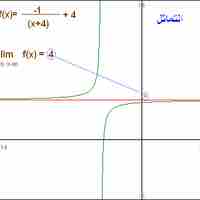
For a real-valued function expressed in terms of other functions, limit values may be computed via algebraic operations.

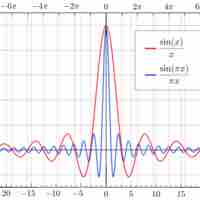
There are several limits of special interest involving trigonometric functions.

For a real-valued continuous function $f$ on the interval $[a,b]$ and a number $u$ between $f(a)$ and $f(b)$, there is a $c \in [a,b]$ such that $f(c)=u$.

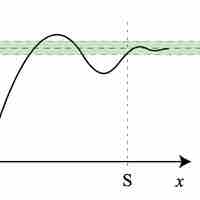
Limits involving infinity can be formally defined using a slight variation of the $(\varepsilon, \delta)$-definition.