Concavity and the Second Derivative Test

In calculus, the second derivative test is a criterion for determining whether a given critical point of a real function of one variable is a local maximum or a local minimum using the value of the second derivative at the point.

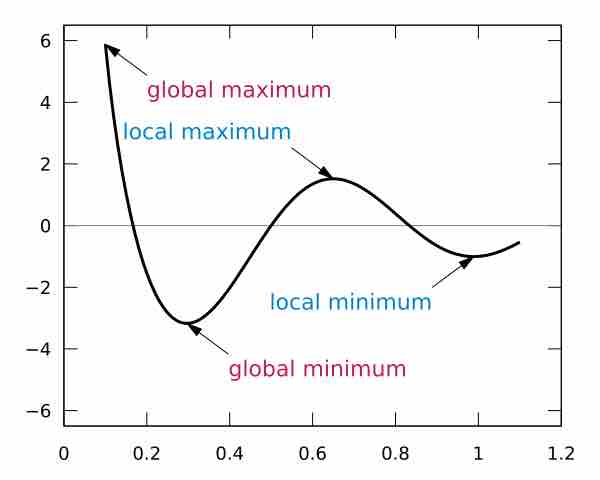
Maxima and Minima

Telling whether a critical point is a maximum or a minimum has to do with the second derivative. If it is concave-up at the point, it is a minimum; if concave-down, it is a maximum.

The test states: if the function $f$ is twice differentiable at a critical point $x$ (i.e. $f'(x) = 0$), then:

If $f''(x) < 0$ then f(x) has a local maximum at $x$.

If $f''(x) > 0$ then f(x) has a local minimum at $x$.

If $f''(x) = 0$, the test is inconclusive.

In the latter case, Taylor's Theorem may be used to determine the behavior of $f$ near $x$ using higher derivatives.

Proof of the Second Derivative Test:

Suppose we have $f''(x) > 0$ (the proof for $f''(x) < 0$ is analogous). By assumption, $f'(x) = 0$. Then,

$\displaystyle{0 < f''(x) = \lim_{h \to 0} \frac{f'(x+h)-f'(x)}{h}}$

Thus, for a sufficiently small $h$ we get

$\displaystyle{\frac{f'(x+h)}{h} > 0}$

which means that $f'(x+h) < 0$ if $h < 0$ (intuitively, $f$ is decreasing as it approaches $x$ from the left), and that $f'(x+h) > 0$  if $h > 0$ (intuitively, $f$ is increasing as we go right from $x$). Now, by the first derivative test, $f(x)$ has a local minimum at $x$.

A related but distinct use of second derivatives is to determine whether a function is concave up or concave down at a point. It does not, however, provide information about inflection points. Specifically, a twice-differentiable function $f$ is concave-up if $f''(x)$ is positive and concave-down if $f''(x)$ is negative.