In mathematics, the maximum and minimum (plural: maxima and minima) of a function, known collectively as extrema (singular: extremum), are the largest and smallest value that the function takes at a point either within a given neighborhood (local or relative extremum) or on the function domain in its entirety (global or absolute extremum).
Maxima and Minima
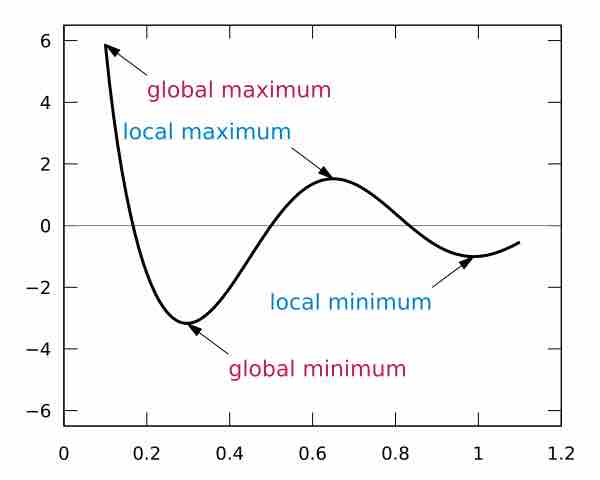
Local and global maxima and minima for
A real-valued function
A function has a global (or absolute) maximum point at
Finding global maxima and minima is the goal of mathematical optimization. If a function is continuous on a closed interval, then by the extreme value theorem global maxima and minima exist. Furthermore, a global maximum (or minimum) either must be a local maximum (or minimum) in the interior of the domain, or must lie on the boundary of the domain. So a method of finding a global maximum (or minimum) is to look at all the local maxima (or minima) in the interior, and also look at the maxima (or minima) of the points on the boundary; and take the biggest (or smallest) one. Local extrema can be found by Fermat's theorem, which states that they must occur at critical points. One can distinguish whether a critical point is a local maximum or local minimum by using the first derivative test or second derivative test.